ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 25
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Цель работы:
1.Исследовать корректирующие свойства и алгоритм работы кодера и декодера Хемминга.
2.Совершенствовать методику проведения экспериментальных исследований и анализа полученных результатов.
3.Прививать навыки работы с вычислительной техникой.
Приборы и оборудование:
1.Персональные компьютеры.
2.Программа схемотехнического моделирования ElectronicsWorkbench
Задание 1. Исследование работы кодера Хемминга
Таблица 1 – Передаваемая комбинация. 7 символов. Комбинация кода Хемминга (11,7).
| Передаваемая комбинация. 7 символов | | i1 | | i2 | i3 | i4 | | i5 | i6 | i7 | |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | |||||
| Проверочные символы | j1 | j2 | | j3 | | j4 | | ||||
| 0 | 0 | 0 | 0 | ||||||||
| Комбинация кода Хемминга (11,7). | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |
Находим проверочные символы:
a1= a3⊕a5⊕a7⊕a9⊕a11=_1_⊕_0_⊕_0_⊕_1_⊕_0_ =_0_
a2 = a3⊕a6⊕a7⊕a10⊕a11 = _1_⊕_0_⊕_0_⊕_1_⊕_1_ = _0_
a4 = a5⊕a6⊕a7 = _0_⊕_1_⊕_1_ = _0_
a8= a9⊕a10⊕a11= _1_⊕_1_⊕_0_ = _0_
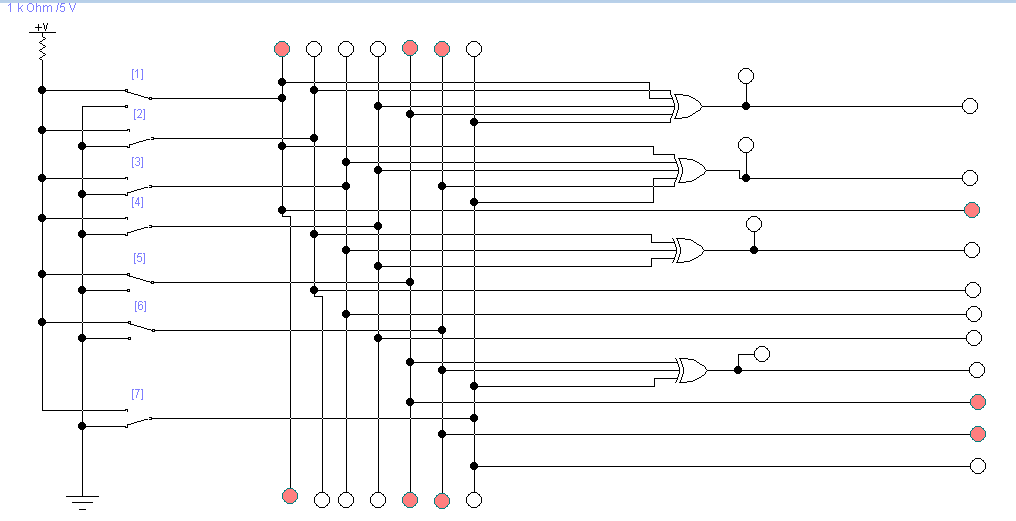
Рисунок 1 − Кодер Хемминга
Задание 2. Исследование работы декодера Хемминга
при отсутствии ошибок (помех) в канале связи.
Таблица 2 – Комбинация кода Хемминга (11,7). Декодер Хемминга . Без ошибки
| j1 | j2 | | j3 | | j4 | | Синдром ошибки | Номер ошибки (дес) | |||||||||||
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | П4 | П3 | П2 | П1 | | ||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | нет | ||||
П1 = a1⊕a3⊕a5⊕a7⊕a9⊕a11 = _0_⊕_1_⊕_0_⊕_0_⊕_1_⊕_0_ = _0_
П2 = a2⊕a3⊕a6⊕a7⊕a10⊕a11 = _0_⊕_1_⊕_0_⊕_0_⊕_1_⊕_0_ = _0_
П3 = a4⊕a5⊕a6⊕a7 = _0_⊕ _0_⊕_0_⊕_0_ = 0__
П4 = a8⊕a9⊕a10⊕a11= _0_⊕_1_⊕_1_⊕_0_ = _0_
S = П4П3П2П1 =_0_ _0_ _0_ _0_
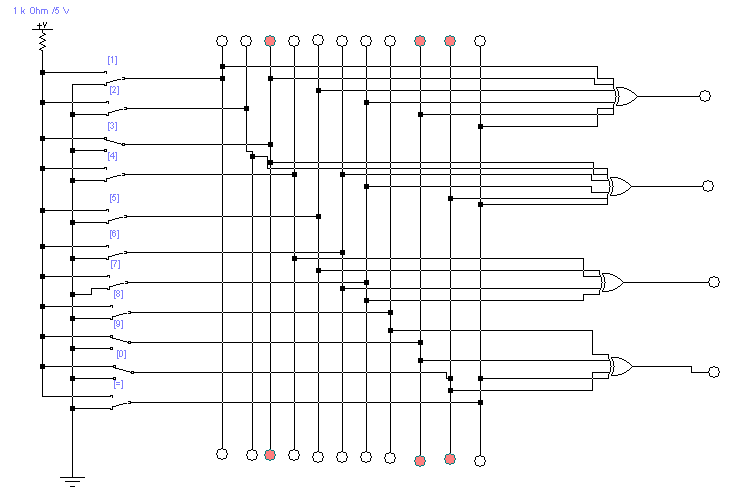
Рисунок 2 − Декодер Хемминга. Прием без ошибки
Задание 3. Исследование работы декодера Хемминга
при наличии ошибок (помех) в канале связи.
Таблица 3.1 – Комбинация кода Хемминга (11,7). Декодер Хемминга. Ошибка в разряде 2
| j1 | j2 | | j3 | | j4 | | Синдром ошибки | Номер ошибки (дес) | |||||||||||
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | П4 | П3 | П2 | П1 | | ||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0(ошибка) 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 7 | ||||
посчитать значения проверок. записать синдром проверки
П1 = a1⊕a3⊕a5⊕a7⊕a9⊕a11 = _0_⊕_1_⊕_0_⊕_1_⊕_1_⊕_0_ = _1_
П2 = a2⊕a3⊕a6⊕a7⊕a10⊕a11 = _0_⊕_1_⊕_0_⊕_1_⊕_1_⊕_0_ = _1_
П3 = a4⊕a5⊕a6⊕a7 = _0_⊕ _0_⊕_0_⊕_1_ = _0_
П4 = a8⊕a9⊕a10⊕a11= _0_⊕_1_⊕_1_⊕_0_ = _0_
S = П4П3П2П1 =_0_ _1_ _1_ _1_
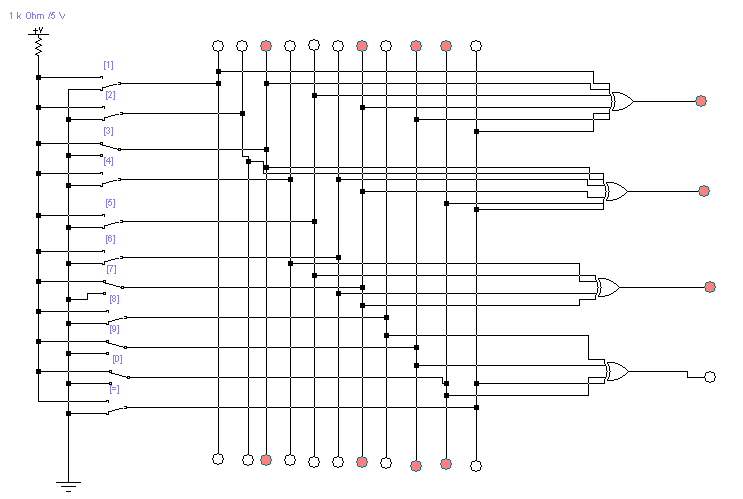
Рисунок 3.1 − Декодер Хемминга с ошибкой в 1 разряде
Таблица 3.2 –Комбинация кода Хемминга (11,7). Декодер Хемминга. Ошибка в разряде 5
| j1 | j2 | | j3 | | j4 | | Синдром ошибки | Номер ошибки (дес) | ||||||||
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | П4 | П3 | П2 | П1 | | |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1(ошибка) 0 | 1 | 0 | 1 | 0 | 0 | 0 | 9 | |
П1 = a1⊕a3⊕a5⊕a7⊕a9⊕a11 = _0_⊕_1_⊕_0_⊕_0_⊕_0_⊕_0_ = _1_
П2 = a2⊕a3⊕a6⊕a7⊕a10⊕a11 = _0_⊕_1_⊕_0_⊕_0_⊕_1_⊕_0_ = _0_
П3 = a4⊕a5⊕a6⊕a7 = _0_⊕ _0_⊕_0_⊕_0_ = _0_
П4 = a8⊕a9⊕a10⊕a11= _1_⊕_0_⊕_0_⊕_0_ = _1_
S = П4П3П2П1 =_1_ _0_ _0_ _1_
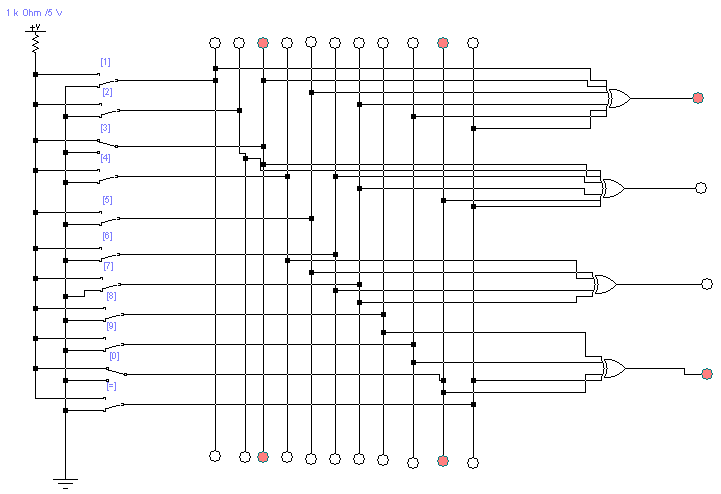
Рисунок 3.2 − Декодер Хемминга с ошибкой в 11 разряде
Вывод
В данной лабораторной работе были исследованы корректирующие свойства и алгоритм работы кодера и декодера Хемминга в программе Electronicks Workbench. В первом задании мы находили проверочные символы a
1= _0_; a2 = _0_; a4 = _0_; a8= _1_ и проверяли в электронной схеме кодера Хемминга. Во втором задании исследовали работы декодера Хемминга при отсутствии ошибок в канале связи, мы считали значения проверок и находили синдром ошибок: П1 =_0_; П2 = _0_; П3 = 0__;П4 = _0_; S = П4П3П2П1 =0 0 0 0 и проверяли в электронной схеме декодера Хемминга. В третьем задании исследовали работы декодера Хемминга при наличии ошибки в канале связи. В начале мы задавали ошибку в разряде 6 и получали синдромы ошибок: П1 = _0_; П2 = _1_;П3 = _1_; П4 = _0_; S = П4П3П2П1 =0 1 1 0, затем задавали ошибку в разряде 11 и получали синдромы ошибок : П1 = _1_; П2 = _1_;П3 = _0_; П4 = _1_; S = П4П3П2П1 =1 1 0 1 и проверяли все расчеты в электронной схеме декодера Хемминга (EWB). Рассмотренный код Хемминга (11,7) обеспечивает исправление всех одиночных ошибок и обнаружение двойных. Это свойство необходимо было исследовано на практике.