ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 949
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; (5.6)
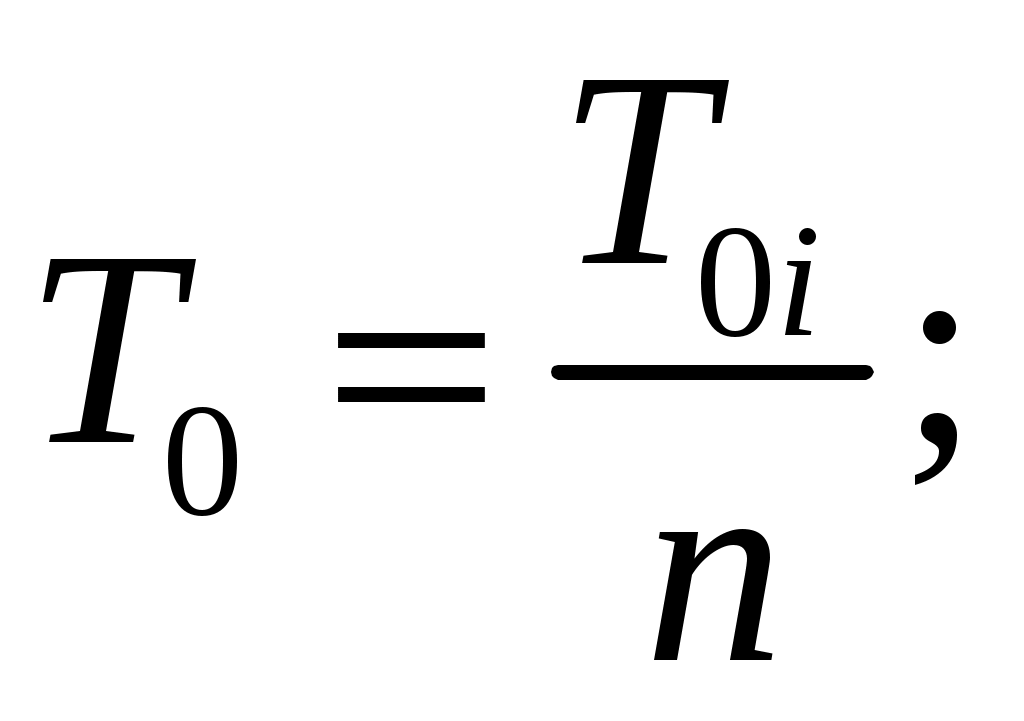(5.7)
т. е. интенсивность отказов в n раз больше, а средняя наработка в n раз меньше, чем у отдельного элемента. При последовательном соединении общая надёжность всей системы ниже надёжности самого слабого элемента. При очень большом количестве высоконадёжных элементов система может оказаться неработоспособной.
Повысить надёжность такой системы можно за счёт выполнения следующих действий:
– увеличения надёжности составных элементов;
– сокращения количества элементов;
– уменьшения интенсивности отказов (за счет уменьшения времени эксплуатации).
Контрольные вопросы и задачи
1. Что такое последовательная система и в чем состоит условие её безотказной работы?
2. Как рассчитывается вероятность безотказной работы систем с последовательным соединением элементов?
3. Как можно повысить надёжность систем с последовательным соединением элементов?
4. Как определяются такие показатели безотказности системы с последовательным соединением элементов, как вероятность безотказной работы и интенсивность отказов?
5. Какой закон распределения наработки до отказа будет иметь система с последовательным соединением элементов, если законы распределения наработки до отказа элементов являются экспоненциальными?
6. Структура проектируемой системы представляется системой с последовательным соединением элементов, состоящей из 10 элементов A, 15 элементов B, 32 элементов D и 8элементов F. Интенсивности отказов элементов известны и равны:
λA = 2 · 10–6 ч–1 , λB = 4 · 10–6 ч–1, λD = 2,5 · 10–6 ч–1, λF = 5 · 10–6 ч–1.
Определить среднюю наработку до отказа T0с и ВБР системы при наработках
t1 = 100 ч, t2= 1000 ч.
Ответ: T0с = 5 · 103 ч, P(t1) = 0,98, P(t2) = 0,819.
5.3. Расчёт надёжности системы
с параллельным соединением элементов
Отказ системы произойдёт при отказе всех элементов (рис. 5.5).
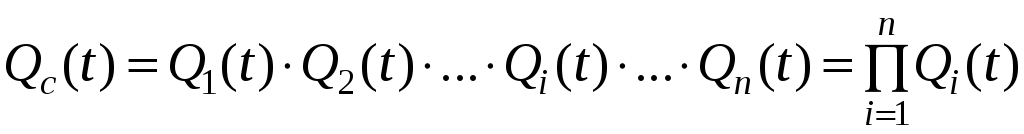, (5.8)
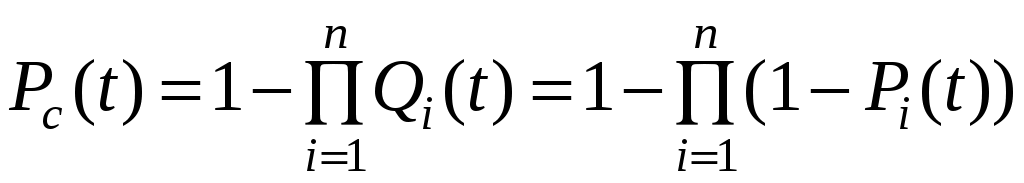. (5.9)
Например, при Pi(t) = 0,86, n = 3 получают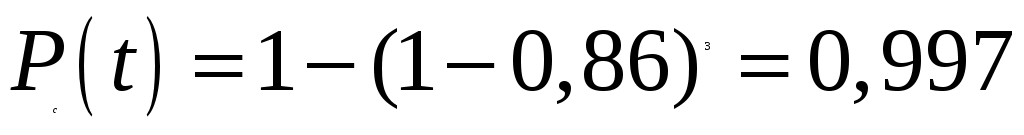
.
Рис. 5.5. Расчетная схема параллельного соединения элементов
При параллельном соединении можно сформировать надёжную конструкцию из самых ненадёжных элементов:
(P(t) + Q(t))m = 1,
где m – количество элементов.
Например, при m = 2: (P(t) + Q(t))m = P2 + 2PQ + Q2 = 1,
здесь P2 означает вероятность безотказной работы обоих элементов;
2PQ– вероятность отказа одного элемента, при этом второй элемент останется работоспособным;
P2 + 2PQ – из строя выйдет (откажет) не более одного элемента;
Q2 – вероятность отказа обоих элементов;
P = Q = 0,5; 0,25 + 0,5 + 0,25 = 1;
при m = 3: (P(t) + Q(t))m =Р3 + 3Р2Q + 3РQ2 + Q3 = 1,
Р3 – все три элемента работоспособны;
3Р2 Q – из строя выйдет не более одного элемента;
3QP2 – из строя выйдет не более двух элементов;
Q3 – из строя выйдут все три элемента.
Из приведенного примера видно, что надёжность системы с параллельным соединением повышается при увеличении числа элементов.
При экспоненциальном распределении наработки выражение (5.9) принимает вид:
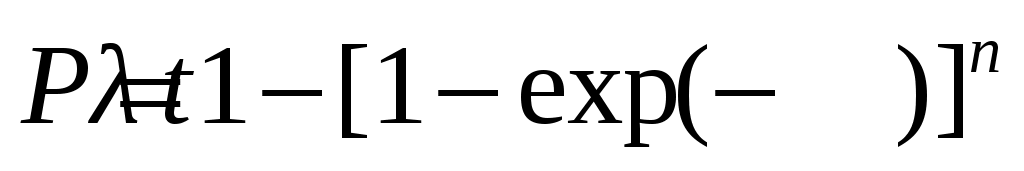, (5.10)
откуда после интегрирования и преобразований средняя наработка системы определяется:
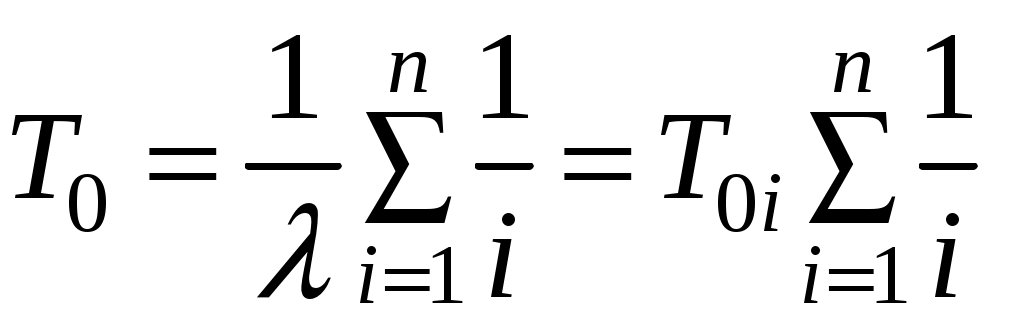, (5.11)
где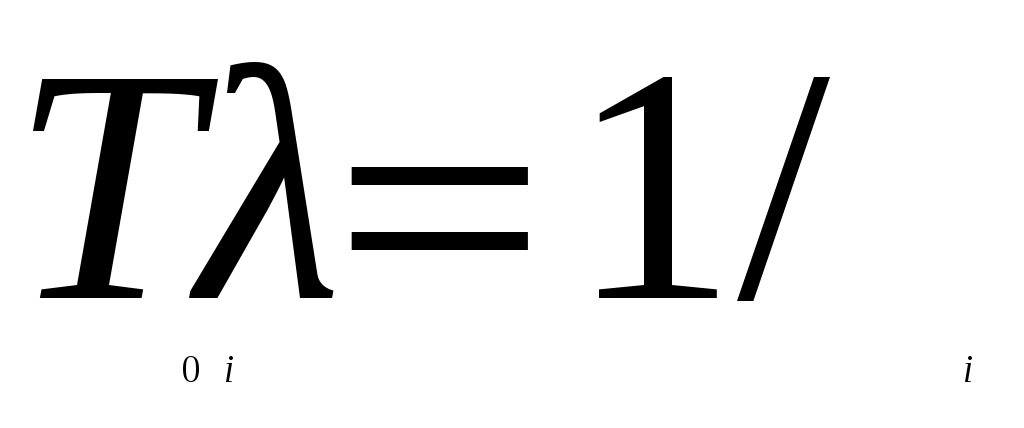
− средняя наработка элемента.
При больших значениях n справедлива приближенная формула
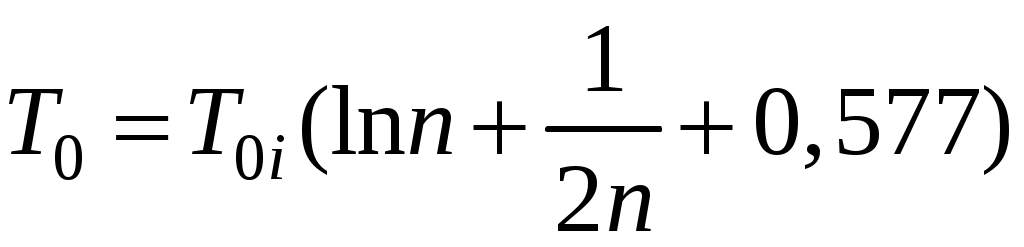. (5.12)
Таким образом, средняя наработка системы с параллельным соединением больше средней наработки её элементов (например, при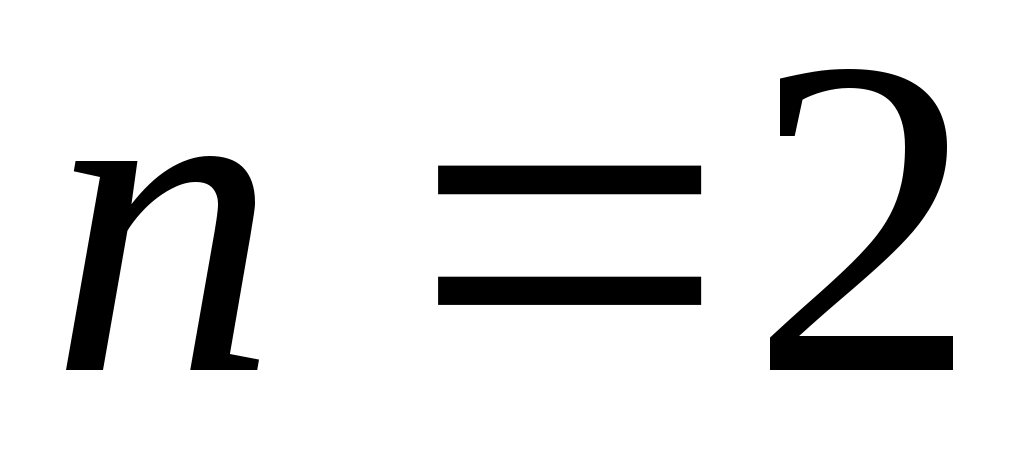
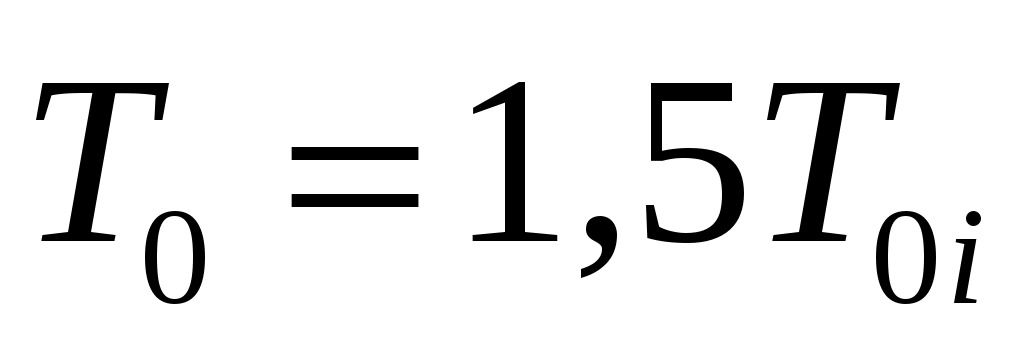, при n= 3 
).
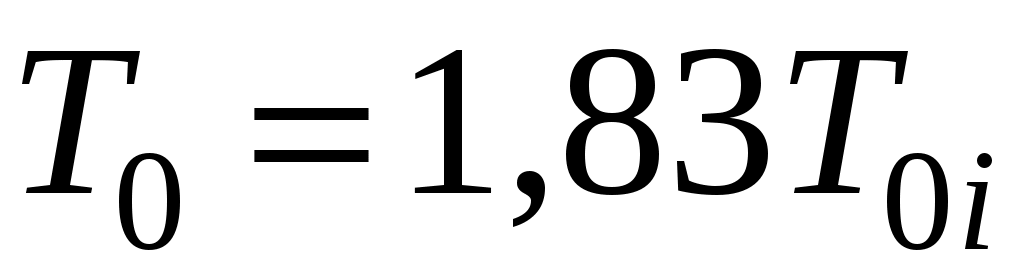Контрольные вопросы
1. Что такое система с последовательным соединением элементов, каковы условия её безотказной работы?
2. Что такое система с параллельным соединением элементов, каковы условия ее безотказной работы?
3. Как рассчитывается вероятность безотказной работы систем с параллельным соединением элементов?
4. Как можно повысить надёжность систем с параллельным соединением элементов?
5. Как определяются такие показатели безотказности системы с параллельным соединением элементов, как вероятность безотказной работы и средняя наработка системы?
5.4. Анализ сложных систем
Проблема эффективности технических систем является одной из основных. Она непосредственно связана с проблемами надёжности и экономичности.
Возрастание сложности технических систем приводит к снижению их надежности, следовательно, к уменьшению их эффективности.
Недостаточная надежность проектируемой или существующей технической системы может стать проблемой, для решения которой нужно выдвинуть альтернативные цели (например, отказ от производства системы или замена ее новой, более совершенной установкой; повышение надёжности существующей системы до требуемого уровня; улучшение условий эксплуатации существующей системы и т. д.).
На практике встречаются системы, для описания которых параллельное или последовательное соединение не годится. В качестве примера показана система, изображённая на рис. 5.6.
Рис. 5.6. Система со сложным соединением элементов
Примерами систем со сложным соединением элементов могут быть дорожная сеть, соединение энергетических систем и др.
В системе, изображённой на рис. 5.6, отказ элемента
А нарушает сразу два пути АС и АД. Таким образом, это соединение не является параллельным. Последовательным такое соединение назвать также нельзя: в случае отказа элемента С система остаётся работоспособной.
Для определения вероятности безотказной работы системы или надёжности функционирования системы используют несколько методов. Рассмотрим самый простой – метод прямого перебора. С помощью этого метода можно определить надёжность работы любого типа технических систем, он легко поддаётся проверке, и, главное, он позволяет рассмотреть влияние отказов элементов на работу системы, т. е. на устойчивость функционирования системы. Недостатком данного метода является громоздкость и трудность в составлении универсальной программы для применения вычислительной техники.
Метод состоит в том, что рассматриваются все возможные способы появления отказов, т. е. не отказал ни один элемент, отказал один элемент, два и т. д.
При рассмотрении системы, изображённой на рис. 5.6, предполагается, что в данном случае элементы системы имеют следующие вероятности безотказной работы:
Р(А) = 0,9; Р(В) = 0,8; Р(С) = 0,6; Р(Д) = 0,7.
Событие А определяется как событие, состоящее в том, что элемент А работает безотказно, тогда Ā – событие, состоящее в том, что элемент А отказал. Аналогично определяются события для всех остальных элементов. Затем вычисляется вероятность состояния системы для каждого способа появления отказа. Результаты всех вычислений записываются в табл. 5.1.
Таблица 5.1
Таблица состояний
Окончание табл. 5.1
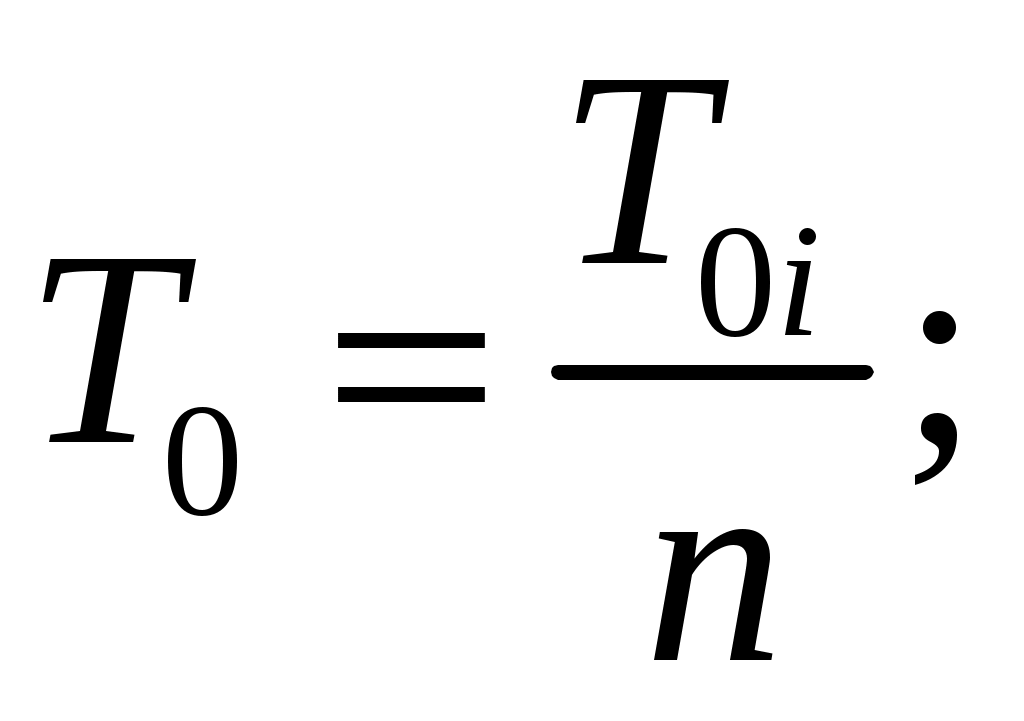(5.7)т. е. интенсивность отказов в n раз больше, а средняя наработка в n раз меньше, чем у отдельного элемента. При последовательном соединении общая надёжность всей системы ниже надёжности самого слабого элемента. При очень большом количестве высоконадёжных элементов система может оказаться неработоспособной.
Повысить надёжность такой системы можно за счёт выполнения следующих действий:
– увеличения надёжности составных элементов;
– сокращения количества элементов;
– уменьшения интенсивности отказов (за счет уменьшения времени эксплуатации).
Контрольные вопросы и задачи
1. Что такое последовательная система и в чем состоит условие её безотказной работы?
2. Как рассчитывается вероятность безотказной работы систем с последовательным соединением элементов?
3. Как можно повысить надёжность систем с последовательным соединением элементов?
4. Как определяются такие показатели безотказности системы с последовательным соединением элементов, как вероятность безотказной работы и интенсивность отказов?
5. Какой закон распределения наработки до отказа будет иметь система с последовательным соединением элементов, если законы распределения наработки до отказа элементов являются экспоненциальными?
6. Структура проектируемой системы представляется системой с последовательным соединением элементов, состоящей из 10 элементов A, 15 элементов B, 32 элементов D и 8элементов F. Интенсивности отказов элементов известны и равны:
λA = 2 · 10–6 ч–1 , λB = 4 · 10–6 ч–1, λD = 2,5 · 10–6 ч–1, λF = 5 · 10–6 ч–1.
Определить среднюю наработку до отказа T0с и ВБР системы при наработках
t1 = 100 ч, t2= 1000 ч.
Ответ: T0с = 5 · 103 ч, P(t1) = 0,98, P(t2) = 0,819.
5.3. Расчёт надёжности системы
с параллельным соединением элементов
Отказ системы произойдёт при отказе всех элементов (рис. 5.5).
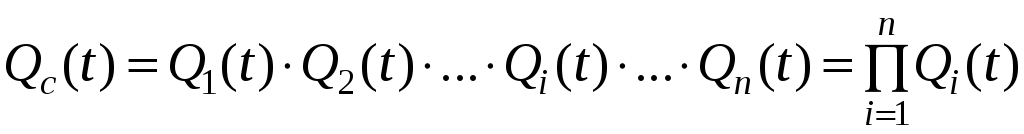, (5.8) 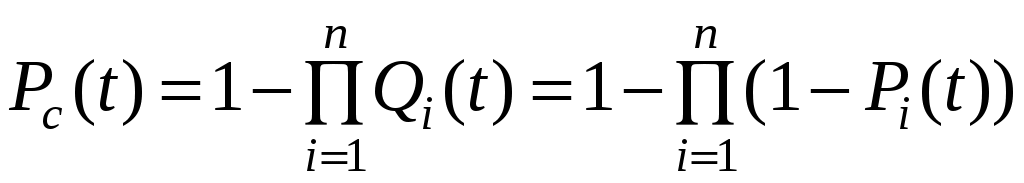. (5.9)Например, при Pi(t) = 0,86, n = 3 получают
. Рис. 5.5. Расчетная схема параллельного соединения элементов
При параллельном соединении можно сформировать надёжную конструкцию из самых ненадёжных элементов:
(P(t) + Q(t))m = 1,
где m – количество элементов.
Например, при m = 2: (P(t) + Q(t))m = P2 + 2PQ + Q2 = 1,
здесь P2 означает вероятность безотказной работы обоих элементов;
2PQ– вероятность отказа одного элемента, при этом второй элемент останется работоспособным;
P2 + 2PQ – из строя выйдет (откажет) не более одного элемента;
Q2 – вероятность отказа обоих элементов;
P = Q = 0,5; 0,25 + 0,5 + 0,25 = 1;
при m = 3: (P(t) + Q(t))m =Р3 + 3Р2Q + 3РQ2 + Q3 = 1,
Р3 – все три элемента работоспособны;
3Р2 Q – из строя выйдет не более одного элемента;
3QP2 – из строя выйдет не более двух элементов;
Q3 – из строя выйдут все три элемента.
Из приведенного примера видно, что надёжность системы с параллельным соединением повышается при увеличении числа элементов.
При экспоненциальном распределении наработки выражение (5.9) принимает вид:
, (5.10)откуда после интегрирования и преобразований средняя наработка системы определяется:
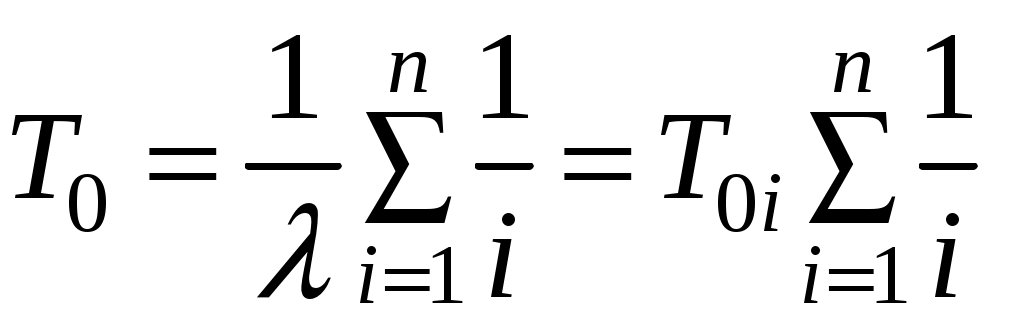, (5.11)где
− средняя наработка элемента. При больших значениях n справедлива приближенная формула
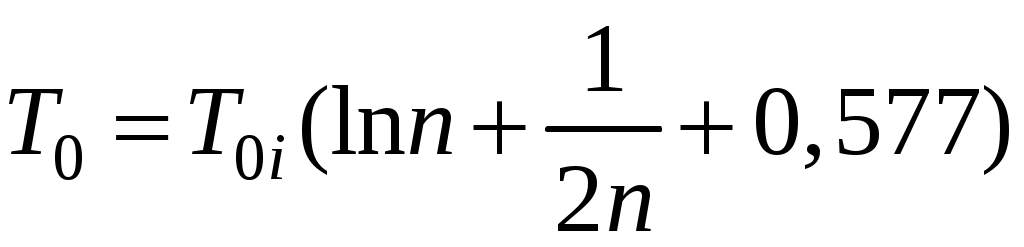. (5.12)Таким образом, средняя наработка системы с параллельным соединением больше средней наработки её элементов (например, при
, при n= 3 ).Контрольные вопросы
1. Что такое система с последовательным соединением элементов, каковы условия её безотказной работы?
2. Что такое система с параллельным соединением элементов, каковы условия ее безотказной работы?
3. Как рассчитывается вероятность безотказной работы систем с параллельным соединением элементов?
4. Как можно повысить надёжность систем с параллельным соединением элементов?
5. Как определяются такие показатели безотказности системы с параллельным соединением элементов, как вероятность безотказной работы и средняя наработка системы?
5.4. Анализ сложных систем
Проблема эффективности технических систем является одной из основных. Она непосредственно связана с проблемами надёжности и экономичности.
Возрастание сложности технических систем приводит к снижению их надежности, следовательно, к уменьшению их эффективности.
Недостаточная надежность проектируемой или существующей технической системы может стать проблемой, для решения которой нужно выдвинуть альтернативные цели (например, отказ от производства системы или замена ее новой, более совершенной установкой; повышение надёжности существующей системы до требуемого уровня; улучшение условий эксплуатации существующей системы и т. д.).
На практике встречаются системы, для описания которых параллельное или последовательное соединение не годится. В качестве примера показана система, изображённая на рис. 5.6.
Рис. 5.6. Система со сложным соединением элементов
Примерами систем со сложным соединением элементов могут быть дорожная сеть, соединение энергетических систем и др.
В системе, изображённой на рис. 5.6, отказ элемента
А нарушает сразу два пути АС и АД. Таким образом, это соединение не является параллельным. Последовательным такое соединение назвать также нельзя: в случае отказа элемента С система остаётся работоспособной.
Для определения вероятности безотказной работы системы или надёжности функционирования системы используют несколько методов. Рассмотрим самый простой – метод прямого перебора. С помощью этого метода можно определить надёжность работы любого типа технических систем, он легко поддаётся проверке, и, главное, он позволяет рассмотреть влияние отказов элементов на работу системы, т. е. на устойчивость функционирования системы. Недостатком данного метода является громоздкость и трудность в составлении универсальной программы для применения вычислительной техники.
Метод состоит в том, что рассматриваются все возможные способы появления отказов, т. е. не отказал ни один элемент, отказал один элемент, два и т. д.
При рассмотрении системы, изображённой на рис. 5.6, предполагается, что в данном случае элементы системы имеют следующие вероятности безотказной работы:
Р(А) = 0,9; Р(В) = 0,8; Р(С) = 0,6; Р(Д) = 0,7.
Событие А определяется как событие, состоящее в том, что элемент А работает безотказно, тогда Ā – событие, состоящее в том, что элемент А отказал. Аналогично определяются события для всех остальных элементов. Затем вычисляется вероятность состояния системы для каждого способа появления отказа. Результаты всех вычислений записываются в табл. 5.1.
Таблица 5.1
Таблица состояний
| № состояния | Число отказавших элементов | События, характеризующие состояние системы | Вероятность состояния системы | Отметка о работоспособности системы, изображённой на рис. 5.6 |
| 1 | 0 |  ∩ ∩ ∩ | 0,3024 | + |
| 2 | 1 |  ∩ ∩ ∩ | 0,0336 | + |
| 3 | 1 | ∩ ∩ ∩ | 0,0756 | + |
| 4 | 1 | ∩ ∩ ∩ | 0,1295 | + |
| 5 | 1 | ∩ ∩ ∩ | 0,2016 | + |
| 6 | 2 | ∩ ∩ ∩ | 0,0084 | – |
Окончание табл. 5.1
| № состояния | Число отказавших элементов | События, характеризующие состояние системы | Вероятность состояния системы | Отметка о работоспособности системы, изображённой на рис. 5.6 |
| 7 | 2 | ∩ ∩ ∩ | 0,0144 | + |
| 8 | 2 | ∩ ∩ ∩ | 0,0224 | – |
| 9 | 2 |  ∩ ∩ ∩ | 0,0324 | + |
| 10 | 2 | ∩ ∩ ∩ | 0,0504 | + |
| 11 | 2 | ∩ ∩ ∩ | 0,0864 | – |
| 12 | 3 | ∩ ∩ ∩ | 0,0036 | – |
| 13 | 3 | ∩ ∩ ∩ | 0,0096 | – |
| 14 | 3 | ∩ ∩ ∩ | 0,0056 | – |
| 15 | 3 | ∩ ∩ ∩ | 0,0216 | – |
| 16 | 4 | ∩ ∩ ∩ | 0,0024 | – |
| | | ∑ | 1,0000 | 0,8400 |