ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 945
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Р и предел прочности на
растяжение s являются случайными величинами, подчиняющимися нормальному закону распределения вероятностей с параметрами соответственно:
Р = 17 800 Н,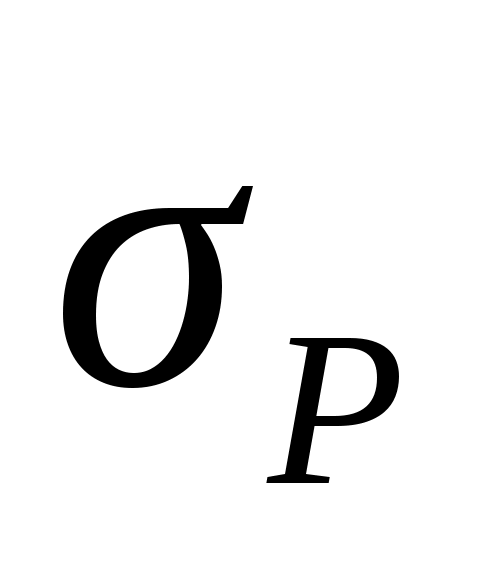 = 445 МПа и s = 690 МПа,
= 445 МПа и s = 690 МПа, 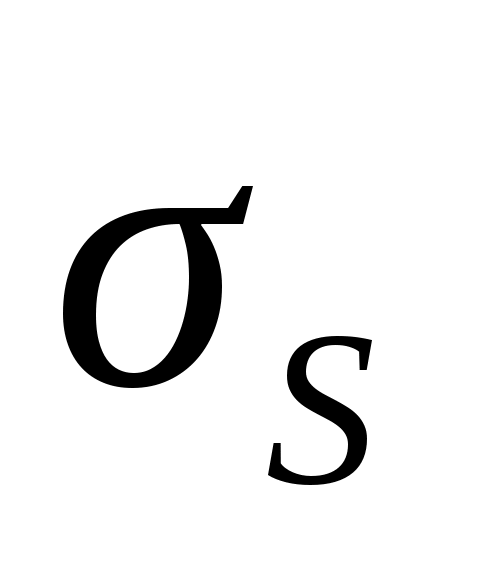 = 34,5 МПа. Заданное значение безотказности R3 = 0,9999.
= 34,5 МПа. Заданное значение безотказности R3 = 0,9999.

Рис. 4.18. Элемент, на который действует растягивающая нагрузка
Решение: растягивающее напряжение определяется по формуле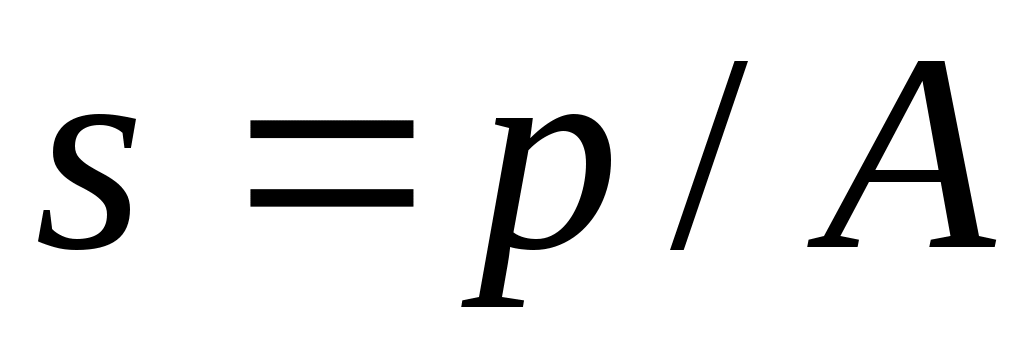 , где
, где 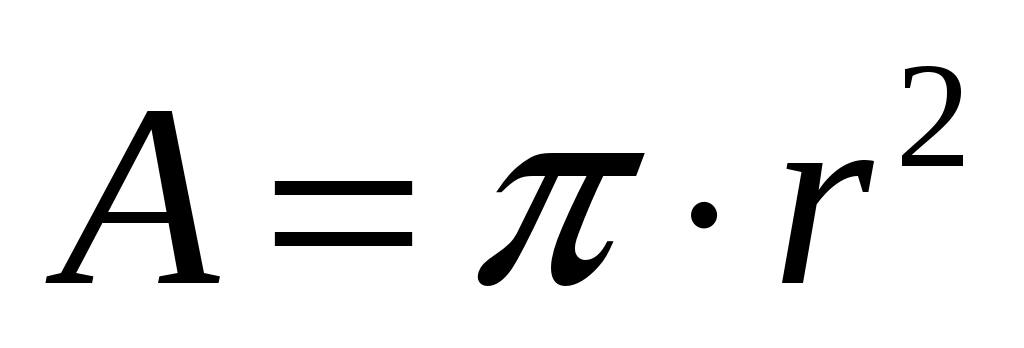 . Допуск на радиус выражается в виде доли
. Допуск на радиус выражается в виде доли 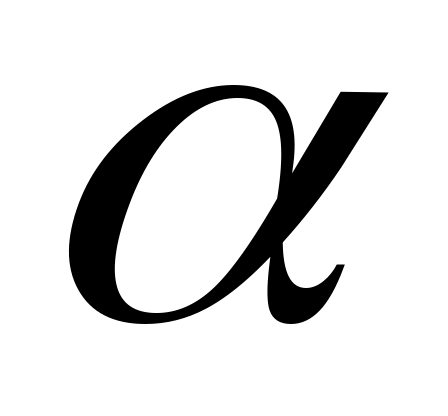 от номинального значения r:
от номинального значения r: 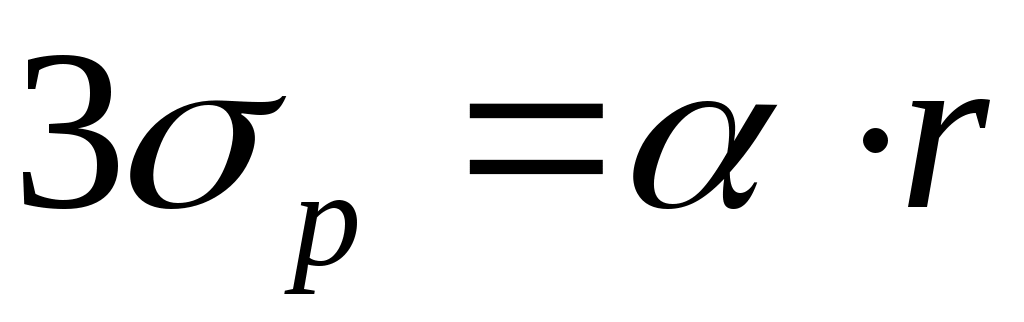 ,
, 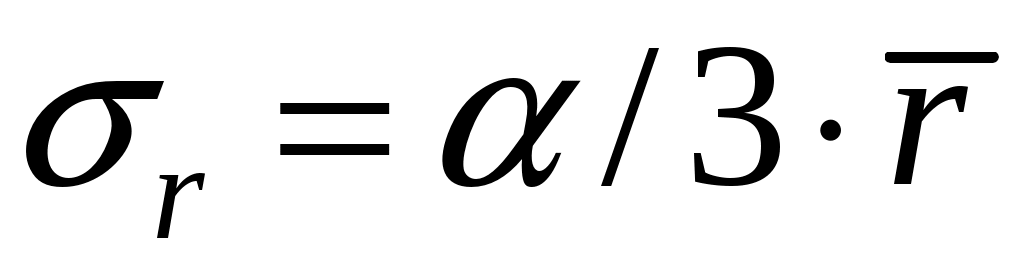 .
.
По формулам расчета математического ожидания и среднеквадратического отклонения линейной функции случайной величины получается: =
=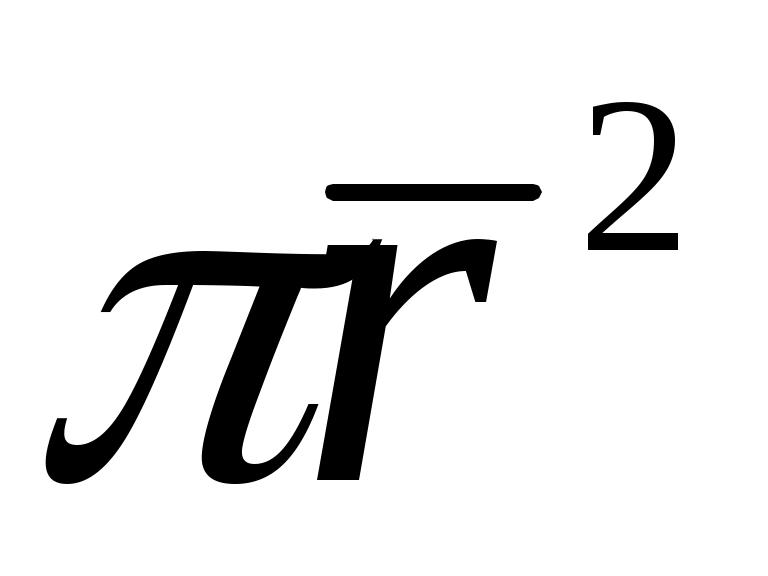 ;
;

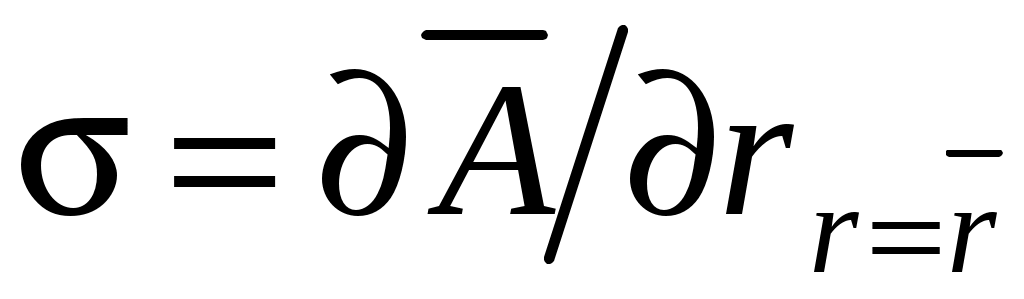 ;
; 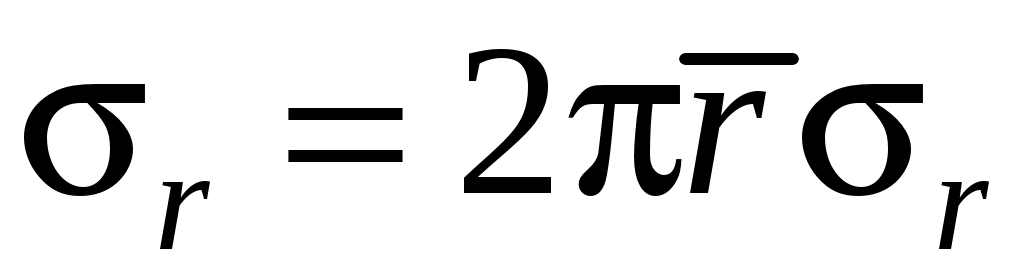 ;
; 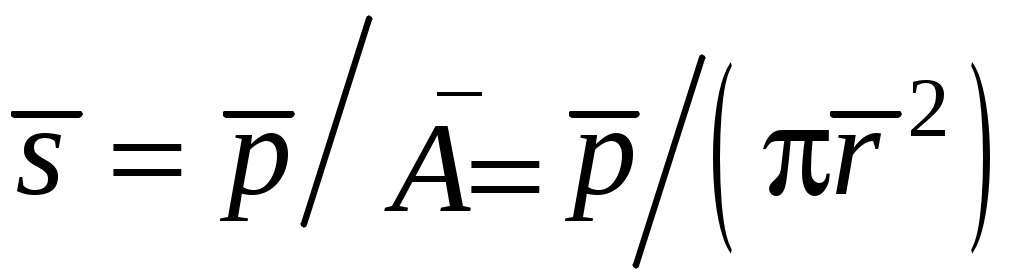 ;
;
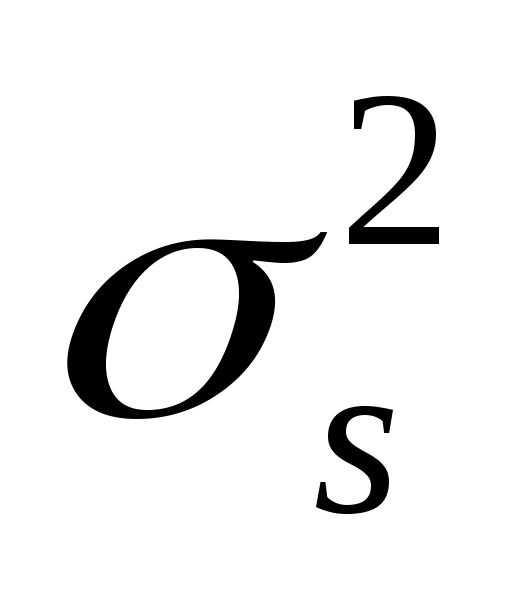 =
=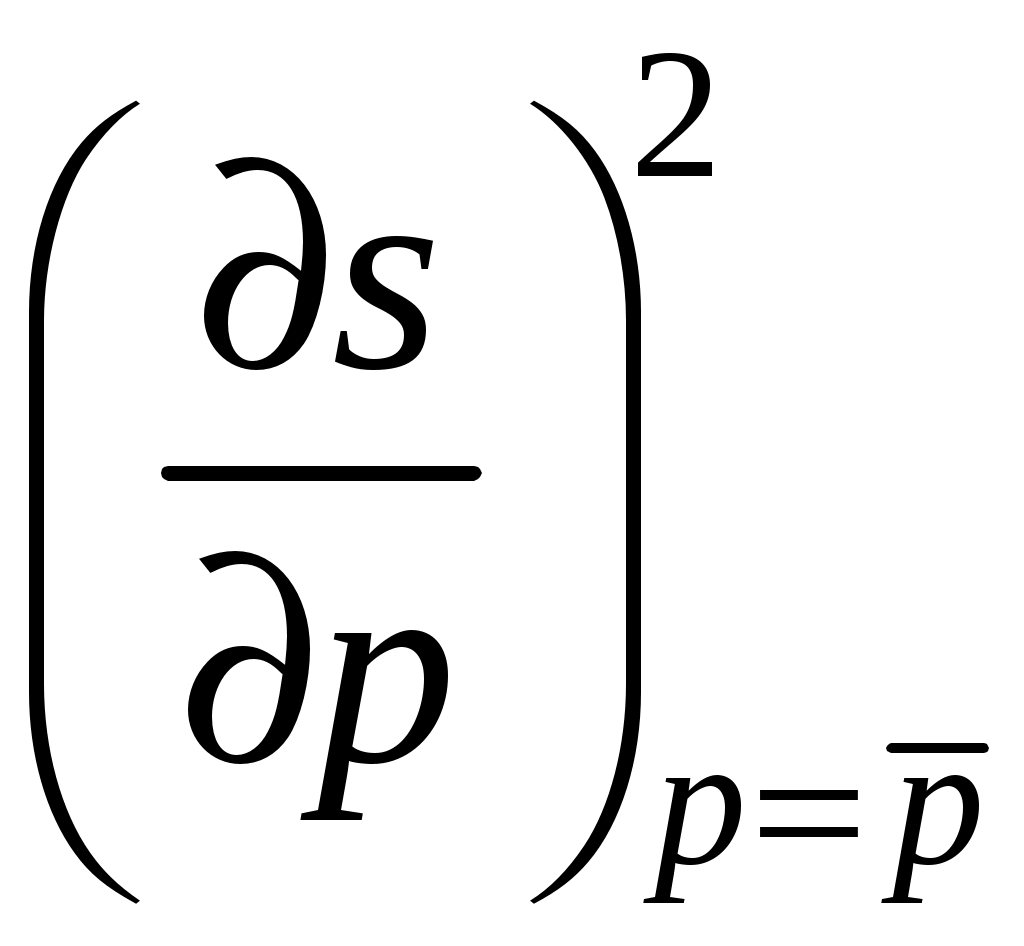 ·
· р+
р+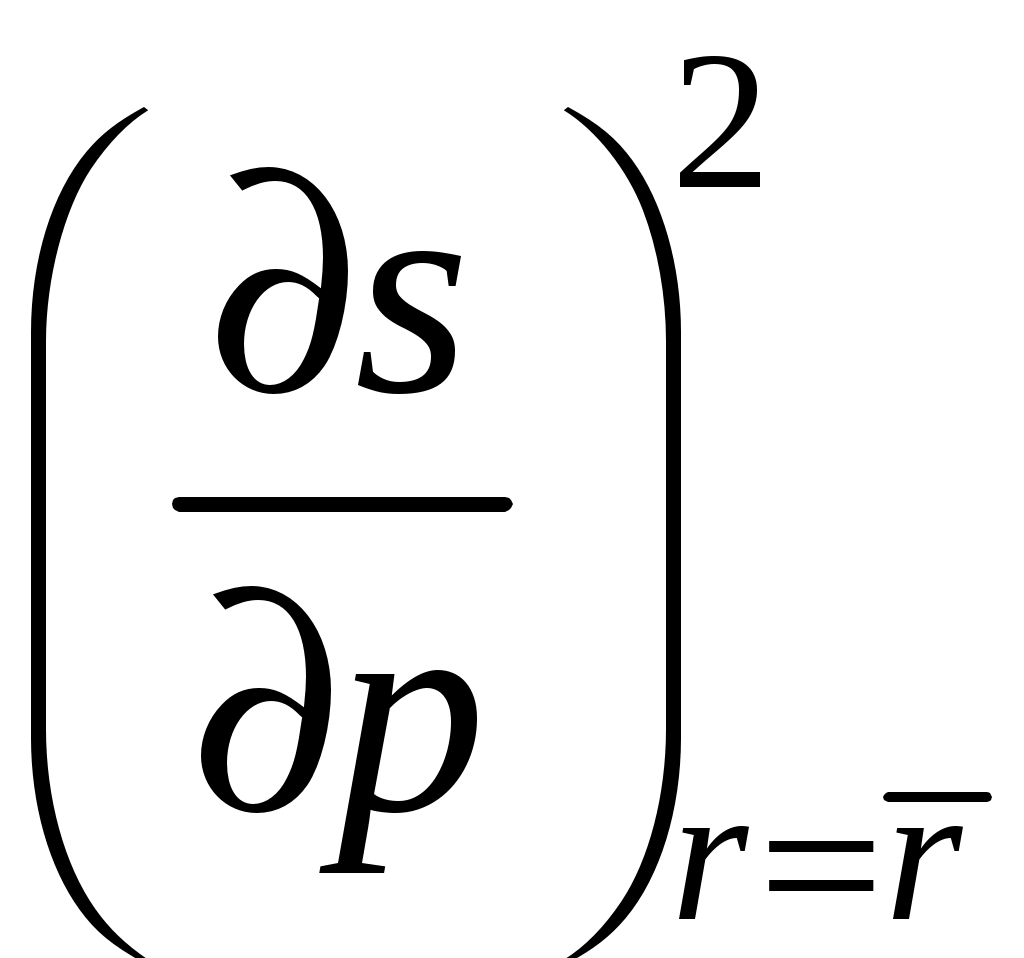 ·
· r =
r =
=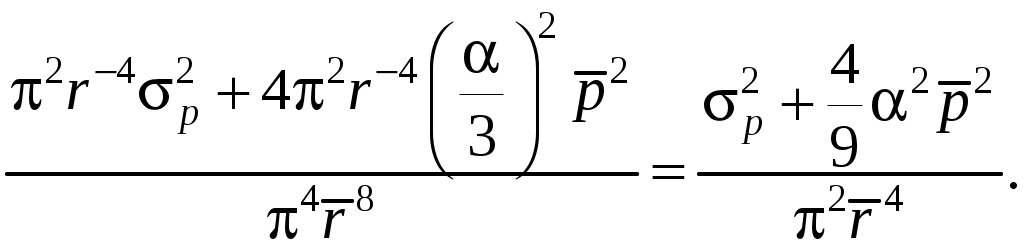
Плотность распределения прочности:
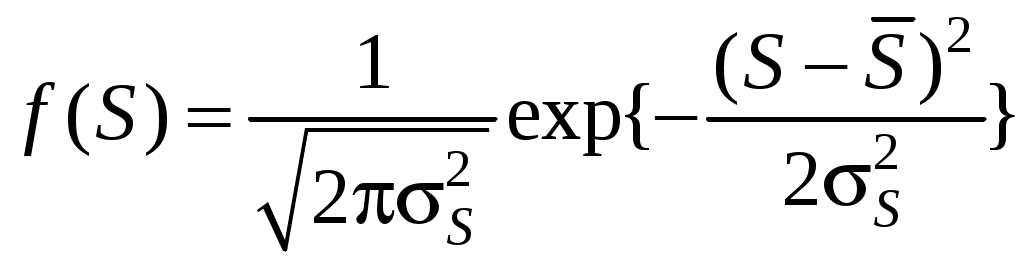
.
Плотность распределения нагрузки:
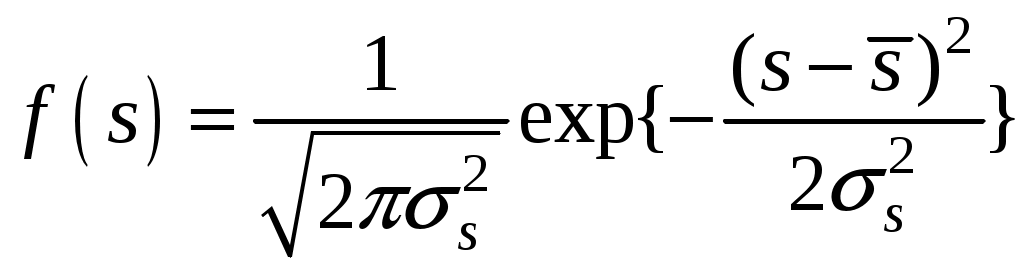 .
.
Плотность распределения разности S – s, соответственно, имеет вид:
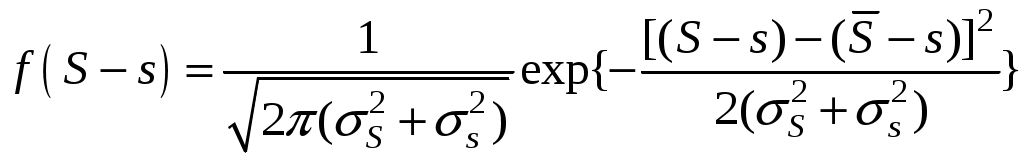 .
.
Условие параметрической безотказности определяется равенством:
R = P{S – s > 0}.
Статистический запас прочности находится из выражения для Р(S – s):
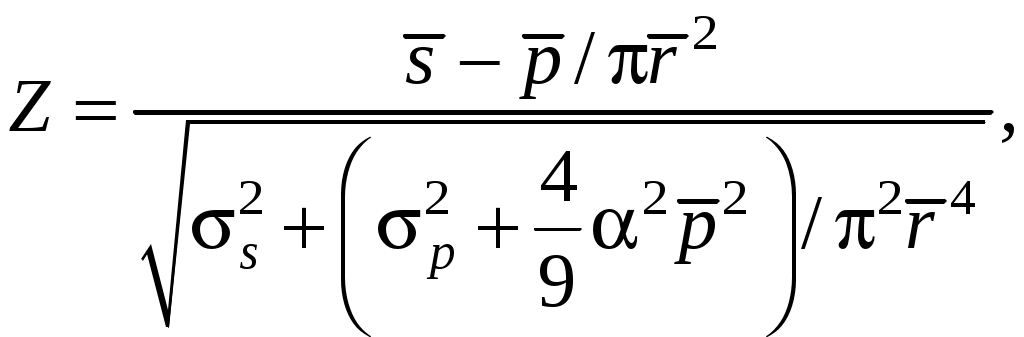
где Z− квантиль стандартного нормального распределения.
Для R3 = 0,9999 по таблицам стандартного нормального распределения находится Z = 3,72. При = 0,015 выполняется равенство
= 0,015 выполняется равенство
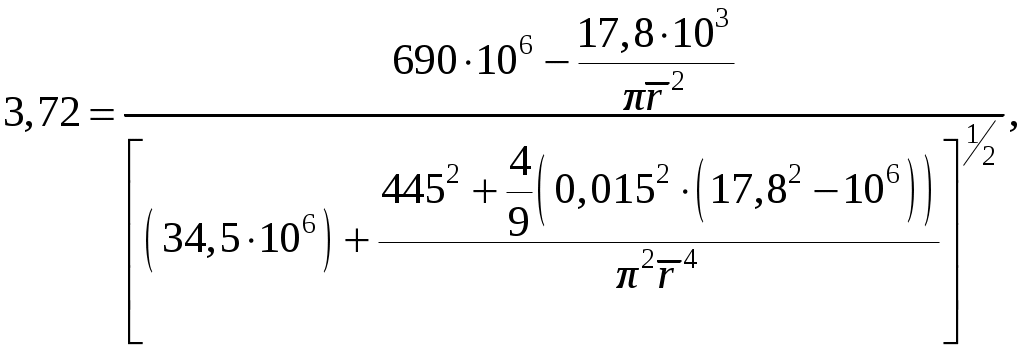
откуда 144,6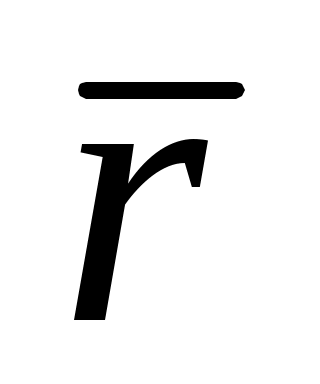 4 – 24,6
4 – 24,6 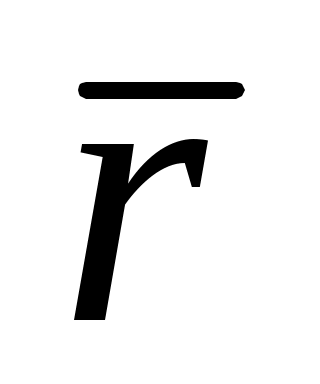 2 + 1 = 0 и окончательно для положительных корней уравнения
2 + 1 = 0 и окончательно для положительных корней уравнения  1 = 2,60 мм;
1 = 2,60 мм;  = 3,21 мм, соответственно R= 0,0001; R = 0,9999.
= 3,21 мм, соответственно R= 0,0001; R = 0,9999.
Влияние допуска и изменчивости прочности материала на надежность элемента представлено в табл. 4.5 и 4.6.
и изменчивости прочности материала на надежность элемента представлено в табл. 4.5 и 4.6.
Таблица 4.6
Влияние прочности материала на надёжность
2. Рассчитать вал, на который действует скручивающая нагрузка Т
(рис. 4.19).
Заданное значение безотказности R3 = 1130 Н·м. Крутящий момент характеризуется параметрами Т = 11 300 Н·м, T = 1130 Н·м. Допустимое срезающее напряжение ограничивается значениями S= 345 МПа,s = 34,5 МПа. Принимается изменчивость радиуса вала r = ( / 3) · .
.

Рис. 4.19. Действие скручивающей нагрузки на вал
Решение: напряжение среза определяется по формуле
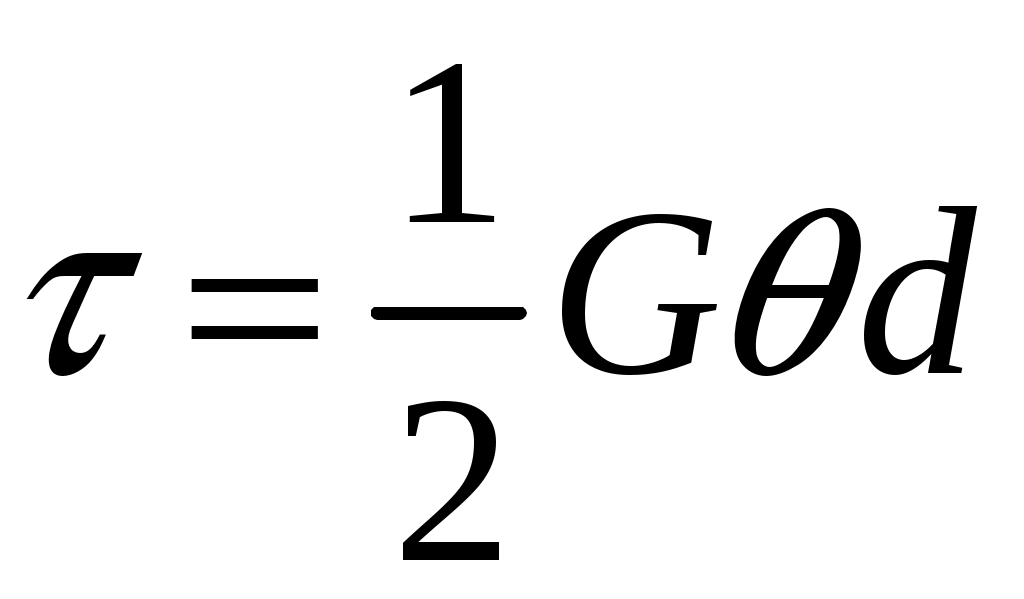 ,
,
где G – модуль упругости; – угол закручивания на единицу длины; d – диаметр вала.
Крутящий момент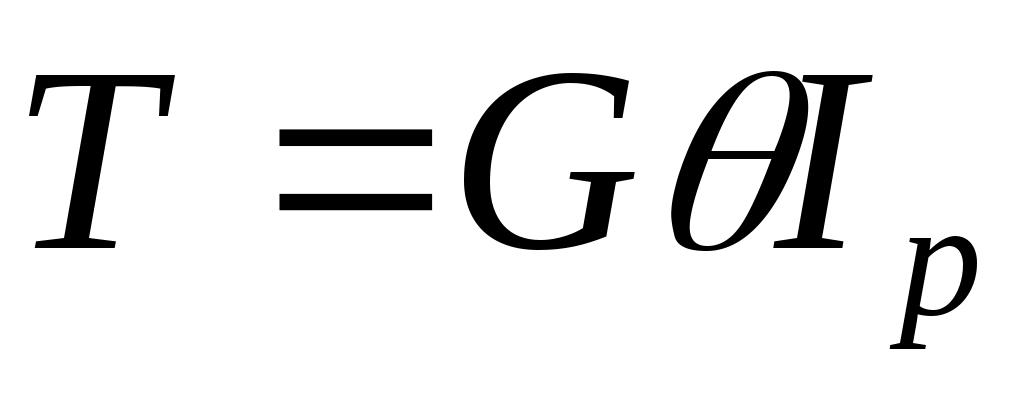 , где Ip – полярный момент инерции вала.
, где Ip – полярный момент инерции вала.
Для круглого вала сплошного сечения
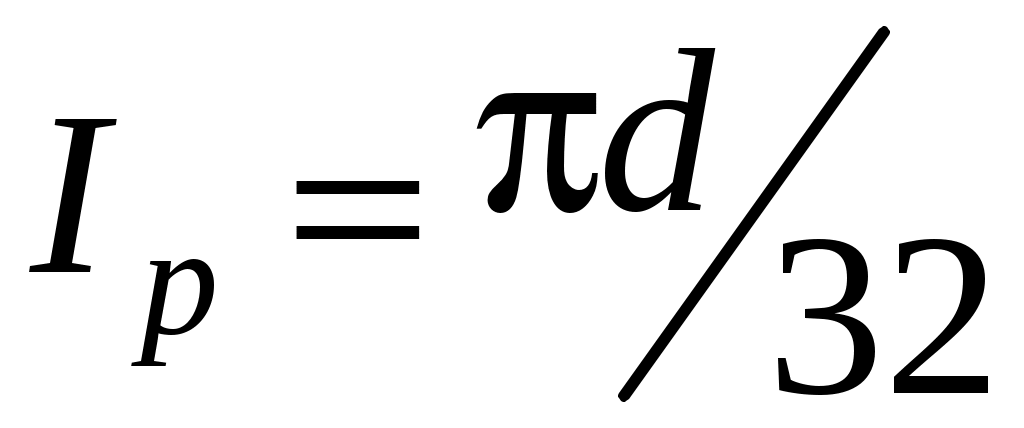 ;
; 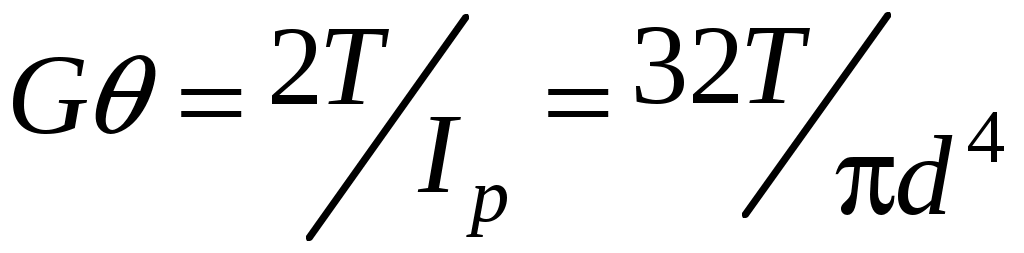 ;
; 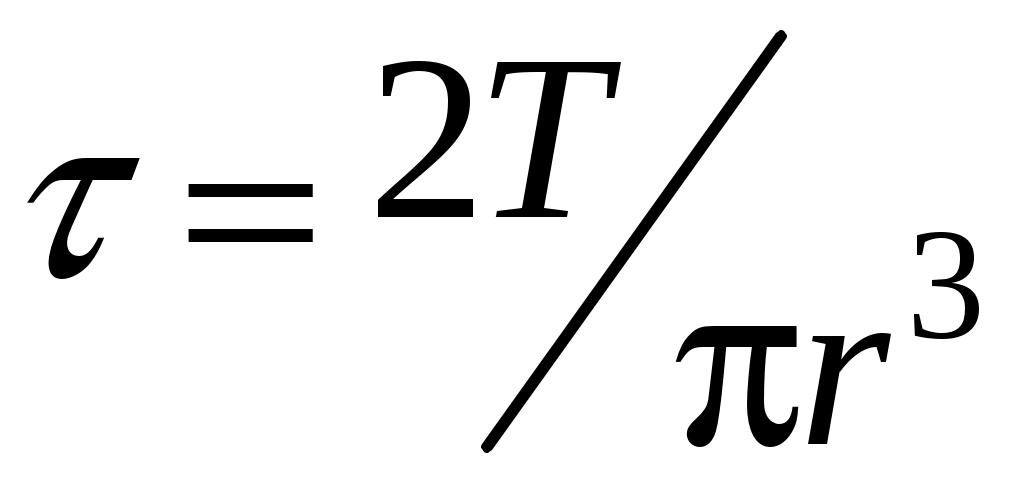 .
.
Применяя приближённые формулы расчёта, получают:
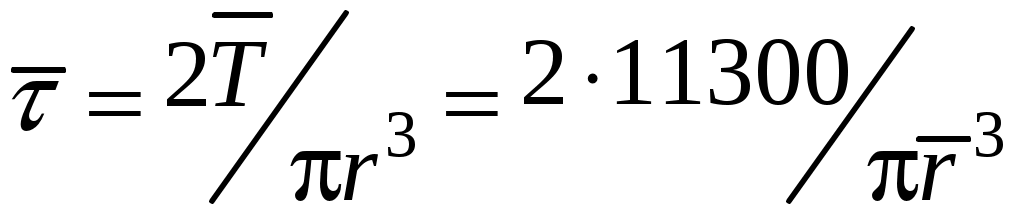 ;
;
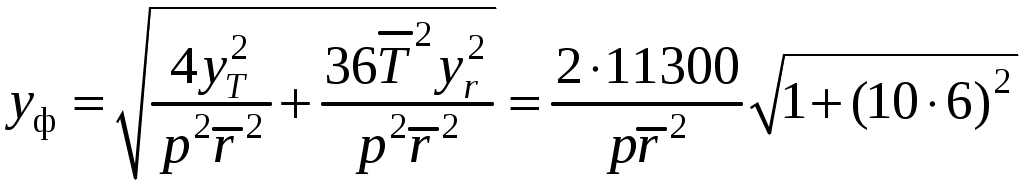 .
.
Для Rз= 0,999 из таблиц стандартного нормального распределения выбирается Z= 3,09. Таким образом,
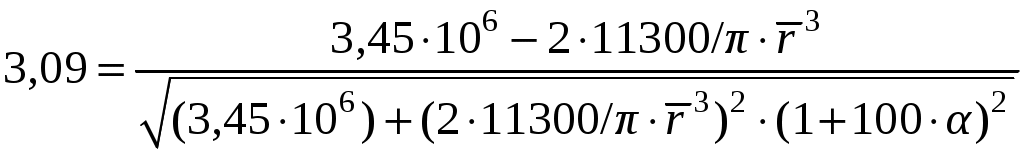 .
.
Выбирая = 0,03, получают: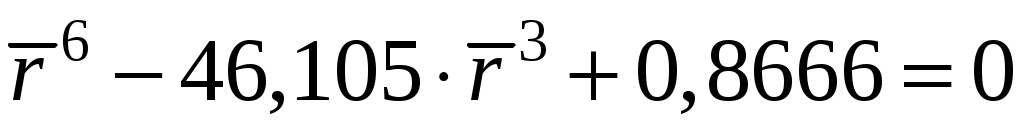 и окончательно для корней уравнения
и окончательно для корней уравнения 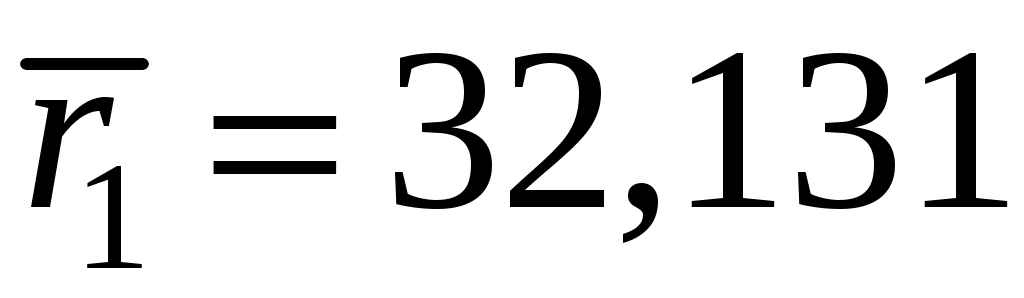 и
и 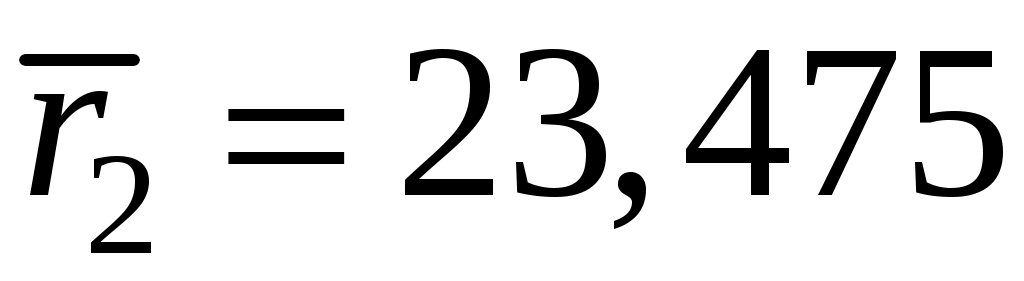 получают соответственно R= 0,999 и R= 0,001.
получают соответственно R= 0,999 и R= 0,001.
Влияние допуска и прочности материала на надёжность R видно из табл. 4.7 и 4.8. В табл. 4.9 показано влияние радиуса вала на надёжность R.
Влияние допуска на надёжность
Таблица 4.8
Таблица 4.9
Влияние радиуса вала на надежность
5. Структурно-логический анализ
технических систем
5.1. Надёжность систем.
Структурная схема надежности системы
Оценка надёжности является одним из элементов сложной системы управления риском, предполагающей выполнение таких работ, как идентификация и анализ риска, оценка пределов его допустимости и возможностей уменьшения путем выбора, осуществления и контроля управляющих действий.
Расчёт надежности технических систем производится с целью выбора лучших конструктивных решений, режимов эксплуатации, организации технического обслуживания и ремонта. Задачами надежности являются определение числовых показателей, выявление наиболее ненадежных элементов, определение наиболее эффективных мер повышения показателей надежности. Решение этих задач возможно после предварительного структурно-логического анализа системы.
растяжение s являются случайными величинами, подчиняющимися нормальному закону распределения вероятностей с параметрами соответственно:
Р = 17 800 Н,

Рис. 4.18. Элемент, на который действует растягивающая нагрузка
Решение: растягивающее напряжение определяется по формуле
По формулам расчета математического ожидания и среднеквадратического отклонения линейной функции случайной величины получается:
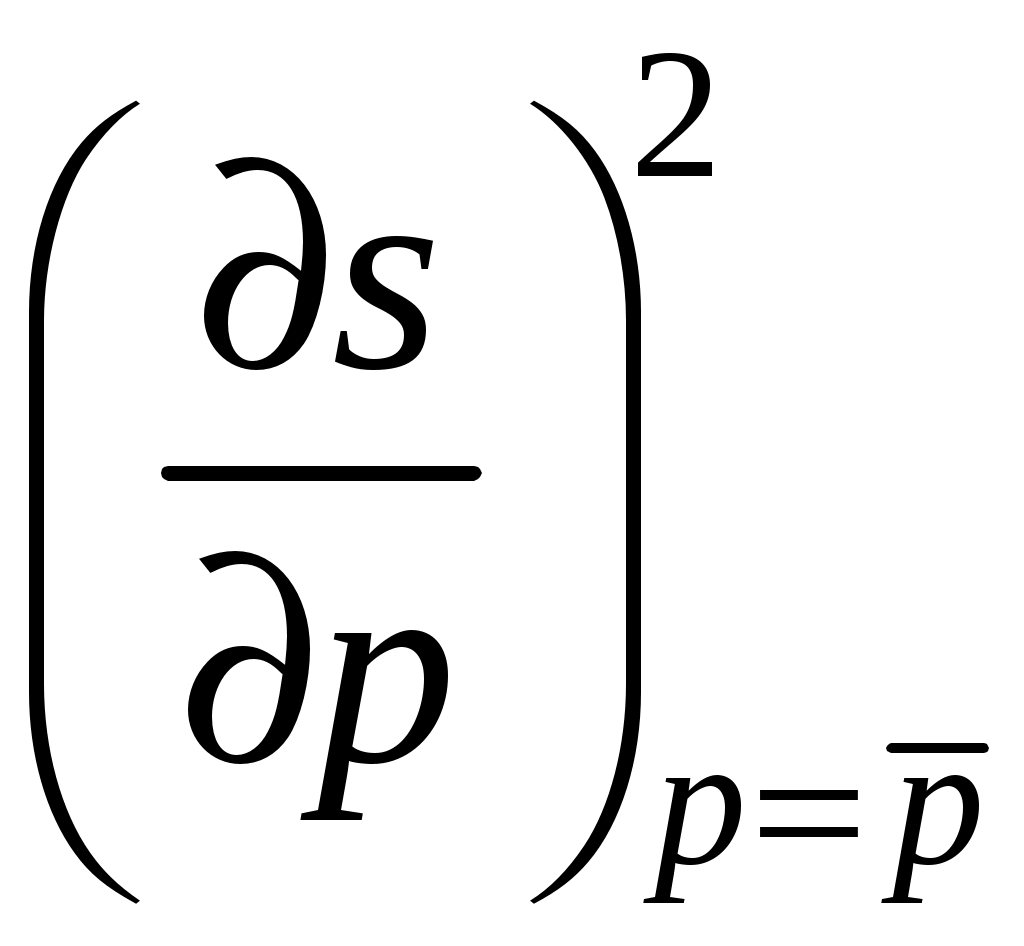 ·
·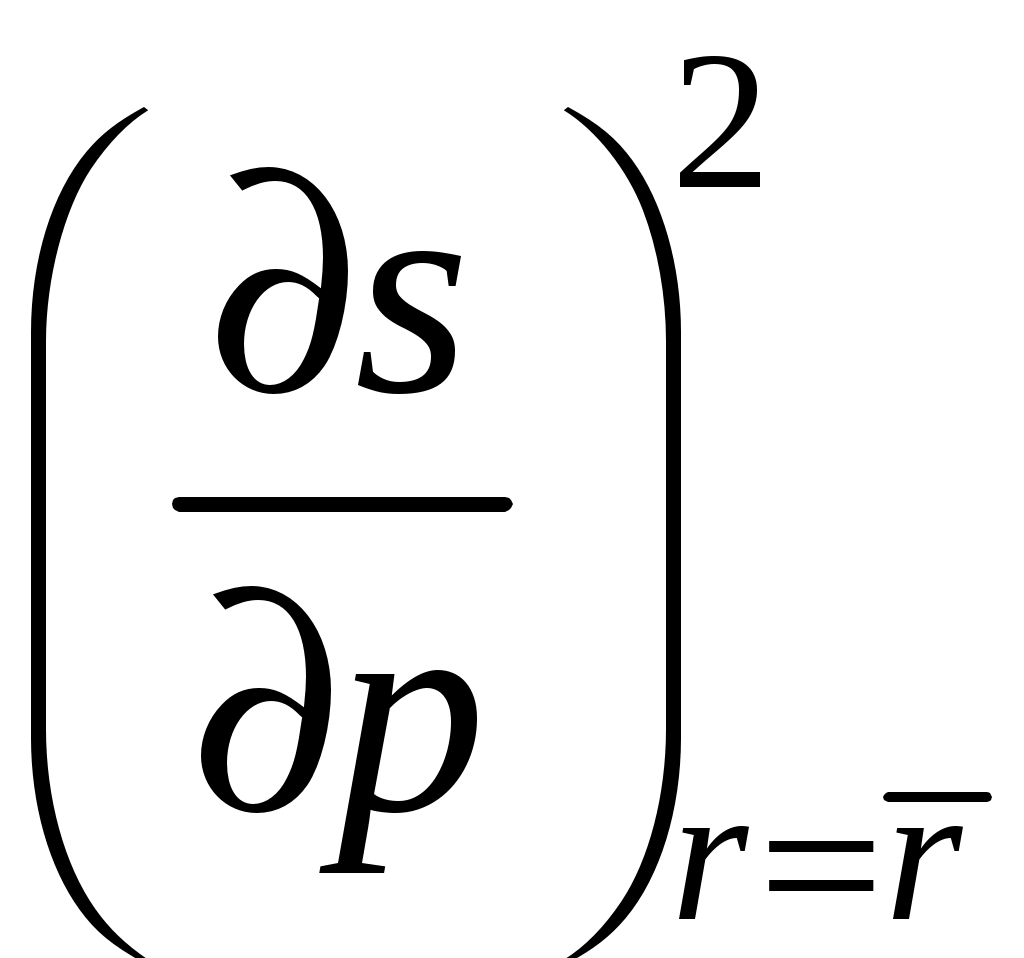 ·
·=
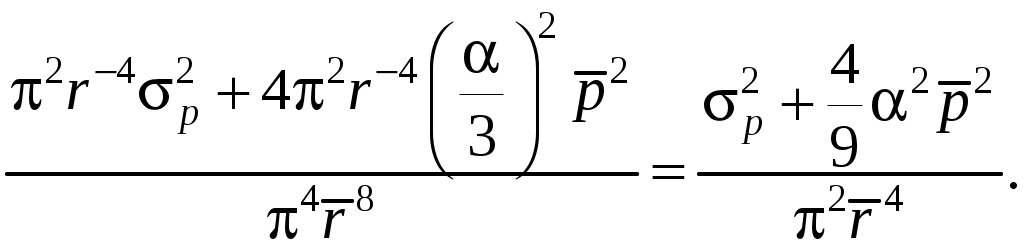
Плотность распределения прочности:
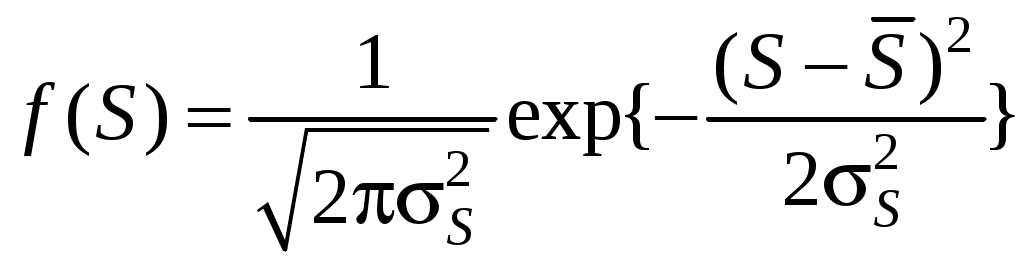
.
Плотность распределения нагрузки:
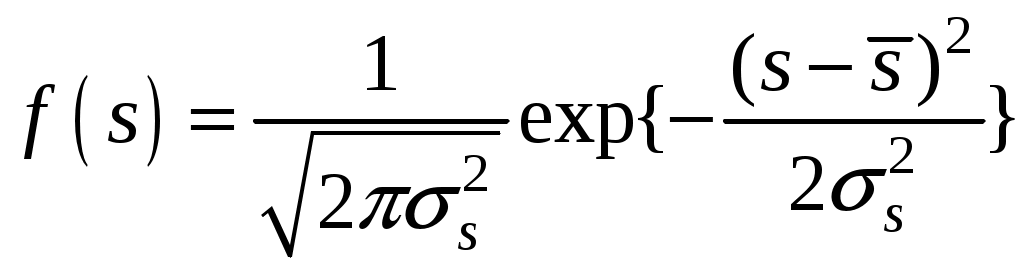 .
.Плотность распределения разности S – s, соответственно, имеет вид:
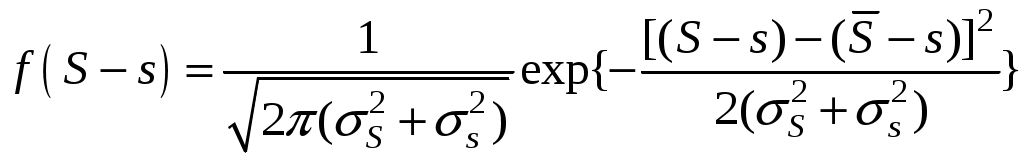 .
.Условие параметрической безотказности определяется равенством:
R = P{S – s > 0}.
Статистический запас прочности находится из выражения для Р(S – s):
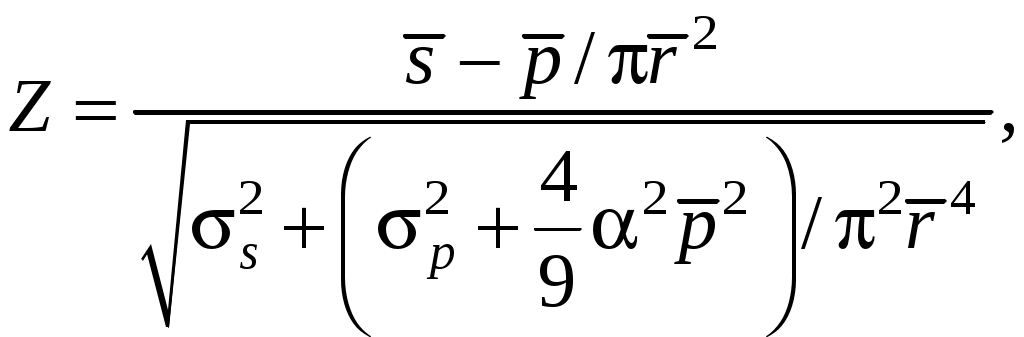
где Z− квантиль стандартного нормального распределения.
Для R3 = 0,9999 по таблицам стандартного нормального распределения находится Z = 3,72. При
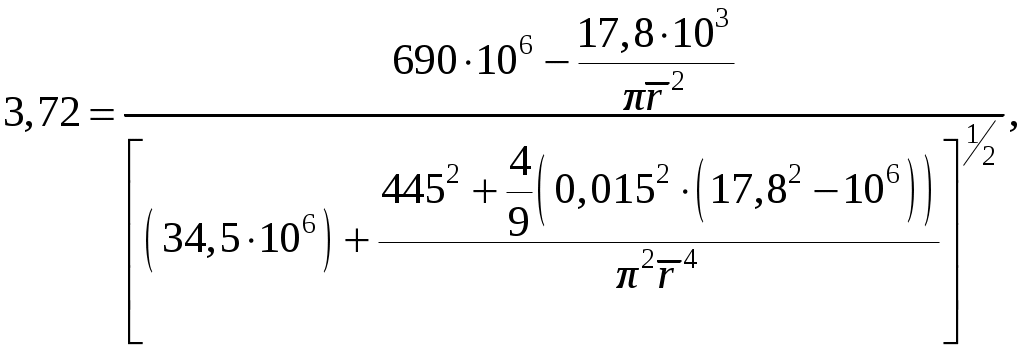
откуда 144,6
Влияние допуска
Таблица 4.5
| | 1,5 | 1,5 | 5 | 7 |
Z | 3,72 | 3,61 | 3,36 | 3,1 |
R | 0,9999 | 0,9998 | 0,9996 | 0,999 |
Влияние допуска на надёжность
Таблица 4.6
Влияние прочности материала на надёжность
| | 34,5 | 41,4 | 48,3 | 55,2 | 62,1 | 68,9 |
| R | 0,9999 | 0,999 | 0,999 | 0,992 | 0,984 | 0,974 |
2. Рассчитать вал, на который действует скручивающая нагрузка Т
(рис. 4.19).
Заданное значение безотказности R3 = 1130 Н·м. Крутящий момент характеризуется параметрами Т = 11 300 Н·м, T = 1130 Н·м. Допустимое срезающее напряжение ограничивается значениями S= 345 МПа,s = 34,5 МПа. Принимается изменчивость радиуса вала r = ( / 3) ·

Рис. 4.19. Действие скручивающей нагрузки на вал
Решение: напряжение среза определяется по формуле
где G – модуль упругости; – угол закручивания на единицу длины; d – диаметр вала.
Крутящий момент
Для круглого вала сплошного сечения
Применяя приближённые формулы расчёта, получают:
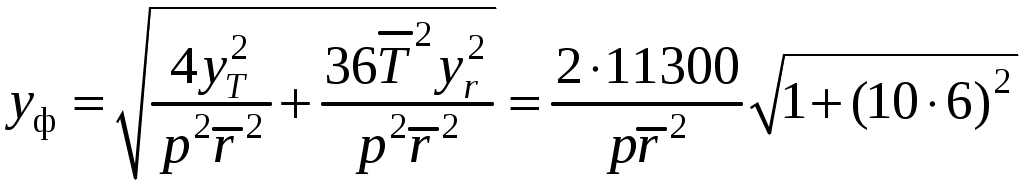 .
.Для Rз= 0,999 из таблиц стандартного нормального распределения выбирается Z= 3,09. Таким образом,
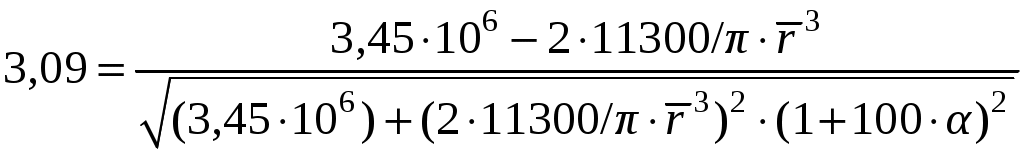 .
.Выбирая = 0,03, получают:
Влияние допуска и прочности материала на надёжность R видно из табл. 4.7 и 4.8. В табл. 4.9 показано влияние радиуса вала на надёжность R.
Таблица 4.7
Влияние допуска на надёжность
| | 3 | 4 | 5 | 10 |
Z | 3,099 | 3,072 | 3,035 | 2,772 |
R | 0,999 03 | 0,9969 | 0,9988 | 0,9974 |
Таблица 4.8
Влияние прочности материала на надежность
| | 34,475 | 41,37 | 55,166 | 68,95 |
Z | 3,099 | 2,712 | 2,145 | 1,763 |
R | 0,999 03 | 0,9964 | 0,984 22 | 0,960 80 |
Таблица 4.9
Влияние радиуса вала на надежность
| | 30,48 | 32,131 | 35,56 | 40,64 |
Z | 2,086 | 3,09 | 4,824 | 6,555 |
R | 0,981 69 | 0,999 | 0,9999 | 0,999 99 |
5. Структурно-логический анализ
технических систем
5.1. Надёжность систем.
Структурная схема надежности системы
Оценка надёжности является одним из элементов сложной системы управления риском, предполагающей выполнение таких работ, как идентификация и анализ риска, оценка пределов его допустимости и возможностей уменьшения путем выбора, осуществления и контроля управляющих действий.
Расчёт надежности технических систем производится с целью выбора лучших конструктивных решений, режимов эксплуатации, организации технического обслуживания и ремонта. Задачами надежности являются определение числовых показателей, выявление наиболее ненадежных элементов, определение наиболее эффективных мер повышения показателей надежности. Решение этих задач возможно после предварительного структурно-логического анализа системы.