МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Сибирский государственный университет науки и технологий

имени академика М.Ф. Решетнева»


Институт заочного обучения

кафедра международного бизнеса

КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Статистика»

Вариант 9


Выполнил: студент группы

БММЗУ20–01

ФИО:
Проверил:
Красноярск 2021

СОДЕРЖАНИЕ



Задание 1. Произвести группировку предприятий по численности работников, приняв следующие интервалы: 1) до 1000 человек; 2) от 1000 до 1300 человек; 3) 1300 человек и более. По каждой группе и в целом по всем предприятиям определить: число предприятий, объем продукции, среднесписочное число работников, среднегодовую стоимость основных средств, а также размер среднегодовой стоимости основных средств в расчете на одного работника и среднюю выработку продукции на одного работника. Результаты группировки представить в виде статистической таблицы. Сформулировать вывод.

№ предприятия	Объем продукции, млн. руб.	Среднегодовая стоимость основных средств, млн. руб.	Среднесписочное число работников, чел.	Прибыль, тыс. руб.
1	197,7	10,0	900	13,5
2	592,0	22,8	1500	136,2
3	465,5	18,4	1412	97,6
4	296,2	12,6	1200	44,4
5	584,1	22,0	1485	146,0
6	480,0	19,0	1420	110,4
7	578,5	21,6	1390	138,7
8	204,7	9,4	817	30,6
9	466,8	19,4	1375	111,8
10	292,2	13,6	1200	49,6
11	423,1	17,6	1365	105,8
12	192,6	8,8	850	30,7
13	360,5	14,0	1290	64,8
14	208,3	10,2	900	33,3

---

Группы предприятий по среднесписочной численности рабочих в отчетном периоде	№ п/п	Среднесписочная численность рабочих	Объем продукции	Среднегодовая стоимость основных средств	Прибыль, тыс. руб.	Размер среднегодовой стоимости основ. средств в расчете на одного работника	Средняя выработка продукции на одного работника
До 1000 чел	1	900	197,7	10,0	13,5	38,4/866,75=0,04	803,3/866,75=0,92
	8	817	204,7	9,4	30,6
	12	850	192,6	8,8	30,7
	14	900	208,3	10,2	33,3
Итого:__3__3690/3=1230__948,9__40,2'>Итого:__4__3467/4=866,75__803,3__38,4'>Итого:	4	3467/4=866,75	803,3	38,4	108,1	0,04	0,92
От 1000 до 1300 чел	4	1200	296,2	12,6	44,4	40,2/1230=0,03	948,9/1230=0,77
	10	1200	292,2	13,6	49,6
	13	1290	360,5	14,0	64,8
Итого:	3	3690/3=1230	948,9	40,2	158,8	0,03	0,77
1300 чел и более	2	1500	592,0	22,8	136,2	140,8/1421=0,09	3590/1421=2,52
	3	1412	465,5	18,4	97,6
	5	1485	584,1	22,0	146,0
	6	1420	480,0	19,0	110,4
	7	1390	578,5	21,6	138,7
	9	1375	466,8	19,4	111,8
	11	1365	423,1	17,6	105,8
Итого:	7	9947/7=1421	3590	140,8	846,5	0,09	2,52

---

Задание 2. Имеются следующие данные по предприятиям фирмы за сентябрь:

Показатель	Предприятия фирмы
	№1	№2	№3
Средняя месячная выработка одного рабочего, тыс. руб.	17,6	18,4	20,8
Удельный вес рабочих предприятия в общей численности рабочих фирмы, %	27,0	35,8	37,2

Определить среднюю месячную выработку рабочих фирмы.

Wм = W1*d, где Wм - средняя месячная выработка рабочих фирмы, тыс. руб.; W1 - Средняя месячная выработка одного рабочего, тыс. руб.; d - Удельный вес рабочих предприятия в общей численности рабочих фирмы, %

№1 - 17,6*27,0 = 475,2 тыс.руб.

№2 - 18,4*35,8 = 658,72 тыс.руб.

№3 - 20,8*37,2 = 773,76 тыс.руб.

Задание 3. Имеются следующие данные о распределении продовольственных магазинов региона по размеру товарооборота за месяц:

Группы магазинов по товарообороту, млн. руб.	Число магазинов
40-50	2
50-60	4
60-70	7
70-80	10
80-90	15
90-100	20
100-110	22
110-120	11
120-130	6
130-140	3

Требуется вычислить средний месячный размер товарооборота магазинов региона, дисперсию и коэффициент вариации.

Рассчитаем средний месячный размер т/о магазинов региона по формуле:

Xм=(xi*fi)/fi,

где    x_i – середина интервала;

f_i – число магазинов.

Составим вспомогательную таблицу:

Группы магазинов по товарообороту млн. руб.	Середина интервала хi	Число магазинов fi	Х∙f	(x-xср)2	(x-xср)2·fi
40-50	45	2	90	2420,6	4841,28
50-60	55	4	220	1536,6	6146,56
60-70	65	7	455	852,6	5968,48
70-80	75	10	750	368,6	3686,4
80-90	85	15	1275	84,6	1269,6
90-100	95	20	1900	0,6	12,8
100-110	105	22	2310	116,6	2566,1
110-120	115	11	1265	432,6	4759,0
120-130	125	6	750	948,6	5691,8
130-140	135	3	405	1664,6	4993,9
	ИТОГО:	100	9420	8426	39935,92

---

Задание 4. В механическом цехе завода в порядке малой выборки изучались фотографии рабочего дня 10 рабочих. Время непроизводительной работы и перерывов, зависящих от рабочего и по организационно-техническим причинам, для обследованных рабочих составило: 52, 48, 60, 46, 62, 54, 51, 49, 55, 53 мин.

Определить: 1) доверительные пределы, в которых находится среднее время непроизводительной работы и перерывов для всех рабочих цеха, гарантируя результат с вероятностью 0,99; 2) вероятность того, что среднее время непроизводительной работы и перерывов всех рабочих цеха отличалось от полученного по выборке не более чем на 3 мин.

1. 
   Среднее время непроизводительной работы и перерывов:
   

Х1=X/n=(52+48+60+46+62+54+51+49+55+53)/10=53 мин.

2. 
   Дисперсия равна:
   

Q²= (Xi-X1)/n = ((52-53)² + (48-53)² + (60-53)² + (46-53)² + (62-53)² + (54-53)² + (51-53)² + (49-53)² + (55-53)² + (53-53)²)/10 = 23,0

Предельная ошибка выборки:

где t – коэффициент доверия (т.к. Р=0,99, то t=3,25).

3. 
   Определяем среднюю ошибку малой выборки:
   

µ_м.в = √ (Q²/n) = √(23,0/10) = √2,3 = 1,51 (мин)

4. 
   Определяем предельную ошибку малой выборки:
   

∆_м.в = t µ_м.в = 3,25*1,51 = 4,9 (мин)

Значение t (3,25) находим из таблицы распределения Стыоденга при числе степеней свободы 9 (n -1) и уровне вероятности 0,99 (уровень значимости 1%).

5. 
   Доверительный интервал будет выглядеть так:
   

48,1(53,0 - 4,9) ≤ Х ≤ 57,9(53,0 + 4,9)

Следовательно, с вероятностью 0,99 можно утверждать, что среднее время простоев по организационно-техническим причинам для всех рабочих цеха находится в пределах от 48,1 до 57,9 мин.

6. 
   В соответствии с нашими расчетами предельная ошибка выборки составила 4,9 мин, т.е. максимальное отклонение среднего время простоев всех рабочих цеха от величины этого показателя, полученного по выборке, не превышает 4,9 мин. Для того чтобы определить, при какой вероятности это расхождение не превысит 3 мин, обратимся к формуле предельной ошибки малой выборки:
   

∆_м.в= t µ_м.в

Если предельная ошибка составляет 3 мин, а средняя ошибка 1,51 мин, то t будет равно 4,53, что соответствует при числе степеней свободы 9 коэффициенту значимости 0,2% или уровню вероятности 0,998. Это значит, что в 998 случаях из 1000 средний уровень простоев рабочих по цеху будет находиться в пределах от 48 до 58 мин.

Задание 5. Имеются следующие данные по 20 предприятиям городского хозяйства об объеме продукции (услуг) за месяц и уровне механизации труда:

---

№ предприятия	Объем продукции (услуг) за месяц, млн. руб.	Уровень механизации, %	№ предприятия	Объем продукции (услуг) за месяц, млн. руб.	Уровень механизации, %
1	90	95	11	65	70
2	77	64	12	95	90
3	80	77	13	90	85
4	90	93	14	91	90
5	91	64	15	100	99
6	100	98	16	110	100
7	101	99	17	109	98
8	105	100	18	107	89
9	110	100	19	89	95
10	99	96	20	98	99

По приведенным данным для выявления наличия связи между объемом продукции и уровнем механизации труда:

1) построить аналитическую таблицу и дать графическое изображение линии связи;

2) измерить тесноту связи между признаками с помощью коэффициента корреляции рангов; проверить его достоверность.

Решение:

Имеем:

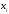- объем продукции за месяц, млн.руб.

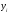- уровень механизации, %.


Рассмотрим исходные данные и отсортируем их по факторному признаку.

Номер п/п	Объем продукции за месяц, млн.руб.	Уровень механизации, %
1	65	70
2	77	64
3	80	77
4	89	95
5	90	95
6	90	93
7	90	85
8	91	64
9	91	90
10	95	90
11	98	99
12	99	96
13	100	98
14	100	99
15	101	99
16	105	100
17	107	89
18	109	98
19	110	100
20	110	100

---

Смотрите также файлы

• Лабораторная работа Гидролиз Выполнение работы Опыт 1.docx

• Курсовая работа по дисциплине Паразитология и ивазионные болезни животных.doc

• " Расчет электрического привода механизма подъема башенного крана".docx

• Тест начат 19052023, 13 11 Состояние Завершены.pdf

• В межрайонную ифнс россии 31 по Республике Башкортостан от Горбуновой Антонины Георгиевны.doc