По полученным данным построим поле корреляции:



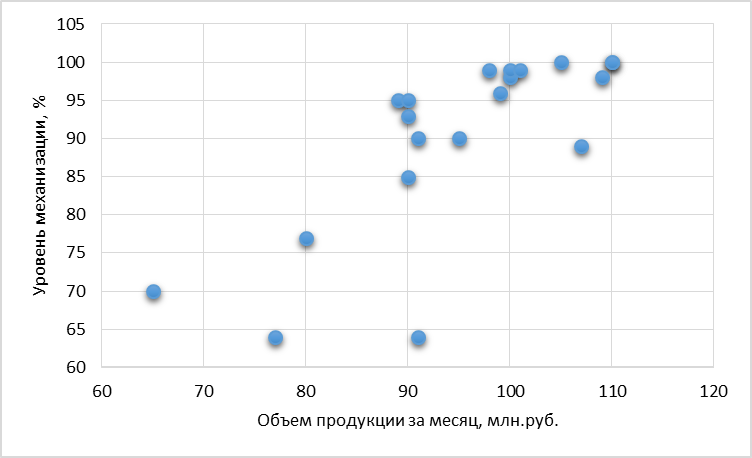
По построенному полю корреляции можно предположить о наличии связи между рассматриваемыми факторами.

Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями.

В качестве меры зависимости признаков X и Y рассмотрим коэффициент ранговой корреляции Спирмена:



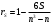
Где:



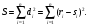
Коэффициент по абсолютной величине ограничен единицей: 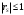и принимает значения 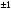в случаях полной предсказуемости одной ранговой последовательности по другой.

Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:

1) Сопоставать каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию).

2) Определить разности рангов каждой пары сопоставляемых значений.

3) Возвести в квадрат каждую разность и суммировать полученные результаты.

4) Вычислить коэффициент корреляции рангов по формуле.

Сопоставим каждому из признаков их порядковый номер (ранг) по возрастанию.

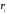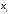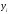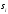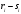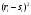1	65	70	3	-2	4
2	77	64	1	1	1
3	80	77	4	-1	1
4	89	95	11	-7	49
5	90	95	12	-7	49
6	90	93	9	-3	9
7	90	85	5	2	4
8	91	64	2	6	36
9	91	90	7	2	4
10	95	90	8	2	4
11	98	99	15	-4	16
12	99	96	12	0	0
13	100	98	14	-1	1
14	100	99	16	-2	4
15	101	99	17	-2	4
16	105	100	18	-2	4
17	107	89	6	11	121
18	109	98	14	4	16
19	110	100	19	0	0
20	110	100	20	0	0

---

Величина S равна:


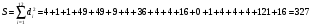
Коэффициент корреляции Спирмена при


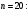
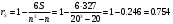
Связь между признаком Y и фактором X сильная

При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные 0,3 и менее, показателями слабой тесноты связи; значения более 0,4, но менее 0,7 - показателями умеренной тесноты связи, а значения 0,7 и более - показателями высокой тесноты связи.

Значимость коэффициента ранговой корреляции Спирмена:



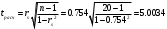
Коэффициент корреляции Спирмена считается статистически значимым, если 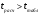, где находится по таблице распределения Стьюдента с параметрами .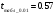



Имеем: 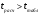, следовательно коэффициент корреляции Спирмена статистически значим.
Задание 6. Число вкладов населения в учреждениях Сберегательного банка России (на начало года)

Год	1992	1993	1994	1995
Число	141,0	203,7	210,9	234,2

Определить ежегодные абсолютные приросты, коэффициенты роста и темпы прироста числа вкладов с постоянной и переменной базой.

Решение:

1. Цепной абсолютный прирост:

∆уц=уt-уt-1,

где yt,t-1 – значение показателя в периоде t и (t-1).

∆1=203,7-141=+62,7 млн.

∆2=210,9-203,7=+7,2 млн.

∆3=234,2-210,9=+23,3 млн.

По сравнению с 1992 г. в 1993 г. число вкладов населения в учреждениях Сбербанка России выросло на 62,7 млн.

По сравнению с 1993 г. в 1994 г. число вкладов населения в учреждениях Сбербанка России выросло на 7,2 млн.

По сравнению с 1994 г. в 1995 г. число вкладов населения в учреждениях Сбербанка России выросло на 23,3 млн.

2. Базисный абсолютный прирост:

∆уб=уt-у0,

где    y0 – значение показателя в базисном периоде.

---

∆1б=203,7-141=+62,7 млн.

∆2б=210,9-141=+69,9 млн.

∆3б=234,2-141=+93,2 млн.

По сравнению с 1992 г. в 1993 г. число вкладов населения увеличилось на 62,7 млн.

По сравнению с 1992 г. в 1994 г. число вкладов населения увеличилось на 69,9 млн.

По сравнению с 1992 г. в 1995 г. число вкладов населения увеличилось на 93,2 млн.

3. Цепной коэффициент роста:

Крц=уt/уt-1

Крц 1=203,7/141=1,44

Крц 2=210,9/203,7=1,03

Крц 3=234,2/210,9=1,11

4. Базисный коэффициент роста:

Крб=уt/у₁

Крб1=203,7/141=1,44

Крб2=210,9/141=1,49

Крб3=234,2/141=1,66

5. Цепной темп прироста:

Т_∆у= (уt/уt-1)/уt-1

Т1=62,7/141=0,44*100=44%

Т2=7,2/203,7=0,03*100=3%

Т3=23,3/210,9=0,11*100=11%

6. Базисный темп прироста:

Т_∆у= (уt/уt-1)/у₁

Т1=62,7/141=0,44*100=44%

Т2=69,9/141=0,49*100=49%

Т3=93,2/141=0,66*100=66%

Задание 7. По предприятию, осуществляющему капитальный ремонт автомобилей КамАЗ, определить общий индекс объема продукции:

Вид продукции	Число ремонтов в прошлом году, ед. q0	Изменение числа ремонтов в текущем году по сравнению с прошлым годом. q1	Сопоставимая цена за единицу продукции. тыс. руб. p0
Капитальный ремонт автомобилей	2500	105	30,0
Капитальный ремонт двигателей	1200	107	8,5
Капитальный ремонт агрегатов	850	98	0,4

I_q=q₁p₀/ q₀p₀ - общий индекс объема продукции

I_q=q₁p₀/ q₀p₀ = (30*105+8,5*107+0,4*98)/(30*2500+8,5*1200+0,4*850) = 4098,70/85540 = 0,04*100% = 4%
Список литературы

1. 
   Джини К. Средние величины. - М.: Статистика, 1970.
   
2. 
   Дрейпер Н., Смит Г. Прикладной регрессионный анализ: В 2-х кн. . – М.: Финансы и статистика, 1986-1987.
   
3. 
   Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы: Учебник. – М.: Финансы и статистика, 2000. – 352 с.
   
4. 
   Дюран Б., Оделл П. Кластерный анализ. - М.: Статистика, 1977.
   
5. 
   Езикиел Н., Фокс К.А. Методы анализа корреляций и регрессий. - М.: Статистика, 1966. 16. Елесеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1997. – 428 с.
   

---

---

Смотрите также файлы

• Лабораторная работа Гидролиз Выполнение работы Опыт 1.docx

• Курсовая работа по дисциплине Паразитология и ивазионные болезни животных.doc

• " Расчет электрического привода механизма подъема башенного крана".docx

• Тест начат 19052023, 13 11 Состояние Завершены.pdf

• В межрайонную ифнс россии 31 по Республике Башкортостан от Горбуновой Антонины Георгиевны.doc