Файл: Контрольная работа По дисциплине Физика Козловская Ольга Алексеевна студент 1 курса группы.docx

Решение:

Судя по условию задачи, и катер, и плоты движутся равномерно.

Когда катер идет вниз по течению, его скорость   складывается со скоростью течения  , и поэтому он проходит расстояние между двумя пунктами быстрее, чем в отсутствие течения, — как, например, если бы он плыл по озеру. Тогда путь S между этими пунктами равен:



Когда же катер идет против течения, оно его тормозит, поэтому он движется медленнее. Теперь его скорость относительно течения, с которой он проходит прежнее расстояние между пунктами, будет равна разности скорости катера и скорости течения. В этом случае тот же путь между пунктами будет равен:



Мы имеем два уравнения и целых четыре неизвестные величины. Но самое главное: мы еще не ввели нужное нам время t, за которое это расстояние проплывут плоты. Здесь следует сообразить, что поскольку плоты несет само течение — ни гребцов, ни двигателя на них нет, — то их скорость равна скорости течения  , и поэтому расстояние S будет равно:



Теперь, глядя на эти три формулы, мы должны сообразить, как бы нам исключить все неизвестные скорости и путь, чтобы остались только времена. Вроде бы решить три уравнения с четырьмя неизвестными величинами нельзя. Но если очень хочется, то иногда можно. Правда, для этого надо хорошенько подумать.

Тогда давайте думать. Что если из формул (1) и (2) выразить сумму и разность скоростей, а потом вычесть из одного полученного уравнения другое. Тогда неизвестная и ненужная нам скорость катера вследствие приведения подобных членов «уйдет», и неизвестных величин станет меньше. Правда, и уравнений тоже станет меньше. Но все равно, надо же как-то решать. Потом посмотрим, что еще можно будет сделать. Итак, приступим:

---

из(1)



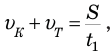
из (2)



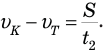
Давайте и из формулы (3) выразим скорость течения — все равно от нее тоже надо «уходить»:



Теперь из левой части равенства (4) вычтем левую часть равенства (5), а из правой — правую. При этом знак равенства не нарушится, но зато скорость катера «уйдет»:



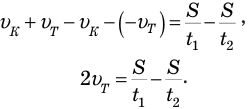
если теперь в равенство (7) подставить вместо скорости течения правую часть равенства (6) и справа вынести путь S за скобки, то он сократится, и у нас останется одно уравнение, в котором будут только одни времена. Приступим. Подставляем в (7) правую часть равенства (6):



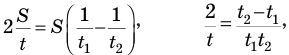
откуда



Мы решили задачу в общем виде. Подставим числа и вычислим:


Ответ: t = 4 ч.


Задача 4. Уравнение движения материальной точки  . В какой координате скорость точки станет равна нулю?
Обозначим х конечную координату точки,   — начальную координату точки, v — конечную скорость точки,   — начальную скорость точки, t — время движения, а — ускорение,   — время, за которое скорость точки уменьшится до нуля,   — координату, в которой скорость точки уменьшится до нуля.

---

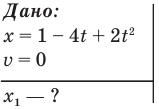
Решение:

Запишем уравнение координаты равноускоренного движения в общем виде:



Теперь сравним это уравнение с уравнением  , данным нам в условии задачи. Из сравнения следует, что проекция начальной скорости точки  , а половина проекции ускорения  ,откуда проекция ускорения  .

Теперь запишем уравнение проекции скорости равноускоренного движения   и подставим в это уравнение числовые значения проекций начальной скорости и ускорения, а конечную скорость, согласно условию, приравняем нулю:  , откуда время, за которое скорость точки уменьшится до нуля,  . Нам осталось подставить значение времени tj = 1 с в данное нам уравнение   и вычислить искомую координату  .
Ответ: х = 7 м.

Задача 5. Тело половину пути прошло со скоростью 36 км/ч, а вторую половину со скоростью 54 км/ч. Найти среднюю скорость на всем пути.
Обозначим   скорость, с которой тело прошло первую половину пути S,   — скорость, с которой тело прошло вторую половину пути S, 

---

 — время прохождения первой половины пути, t — время прохождения второй половины пути,   — среднюю скорость на всем пути.


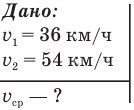
Решение:

Средняя скорость равна отношению всего пути S ко времени прохождения первой половины пути   со скоростью   плюс время прохождения второй половины пути   со скоростью  :



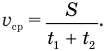
Здесь  .

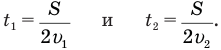Подставим эти равенства в знаменатель первой формулы:


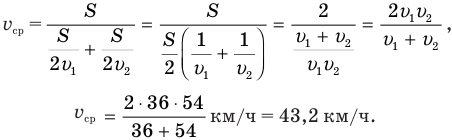
Ответ:   = 43,2 км/ч.


Задача 6. Мяч упал с высоты   м, отскочил от пола и был пойман на высоте   м. Чему равен путь   и модуль перемещения   тела?
Дано: 

 м
 м

Найти: 

---

 -?

 — ?

 

Решение

Думаем: вопрос задачи относится к траектории движения. Такого типа задачи лучше всего начинать с рисунка (рис. 1).



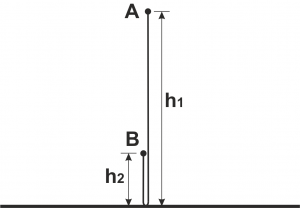
Рис. 1. Траектория движения.

Для удобства, виртуально разделим движение вдоль одной прямой (мяч летит вдоль этой прямой) на два движения и нарисуем линии немножко разнесёнными друг относительно друга. Занесём на рисунок все параметры, которые фигурируют в дано. Для приведенного рисунка точка А — точка начала движения, точка B — конец движения.

Решаем: перейдём к вопросам задачи: как ни странно это звучит, если необходимо что-то найти, нужно знать, что мы ищем. Обратимся к первому вопросу: чему равен путь   тела? По определению, путь — скалярная физическая величина, численно равная длине траектории, т.е. для нахождения пути необходимо найти расстояние, пройденное телом за интересующее время движения. Исходя из этого определения, наш путь — это расстояние от точки A до пола и от пола до точки B:

 (1)



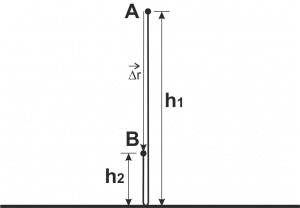
Рис. 2. Нахождение перемещения

В правой части уравнения известны все параметры, значит, мы можем найти искомое значение (пока не ищем). Перейдём ко второму вопросу: чему равен модуль перемещения   тела? По определению, перемещение — векторная физическая величина — вектор, соединяющий начальную и конечную точку движения. Т.е. для нахождения перемещения необходимо найти модуль вектора перемещения (длину этого вектора) и направление данного вектора. В нашем случае, это вектор, соединяющий начало движения (точка А) и конец движения (точка B). Нарисуем этот вектор (рис. 2). В данном векторе нас интересует его модуль, т.е. длина. Из рисунка видно, что:

---