Файл: Контрольная работа По дисциплине Физика Козловская Ольга Алексеевна студент 1 курса группы.docx

 (2)

И опять в правой части уравнения всё известно. Таким образом, вы можем посчитать все интересующие нас параметры задачи.

Считаем: и не забываем про размерности:

 (м)

 (м)
Ответ:   (м),   (м).

Задача 7. Спортсмен на тренировке пробежал   кругов радиусом   м каждый. Какой путь пробежал спортсмен? Чему равен модуль его перемещения?
Дано: 



 м
Найти: 

 -?

 -?
Решение



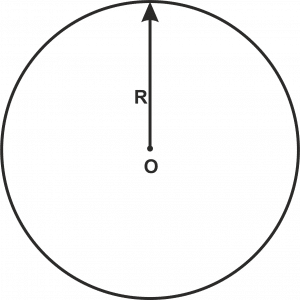
Рис. 1. Траектория движения тела

В рамках нашего дано не указаны переменные, которые обозначают то, что нам нужно найти. Давайте введём эти обозначения: пусть   — путь, проделанный телом,   — модуль перемещения тела.  Собственно, вопрос задачи относится к траектории движения. Такого типа задачи лучше всего начинать с рисунка (рис. 1).
Решаем: траектория движения тела — окружность. Обратимся к первому вопросу задачи: по определению, путь — скалярная физическая величина, численно равная длине траектории, т.е. для нахождения пути необходимо найти расстояние, пройденное телом за интересующее время движения. Исходя из условий задачи,

---

тело прошло путь, равный заданному количеству длин окружностей ( ), т.е.:

 (1)

В правой части уравнения известны все параметры, значит, мы можем найти искомое значение (пока не ищем).



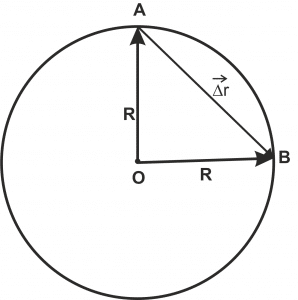
Рис. 2. Перемещение
Перейдём ко второму вопросу: чему равен модуль перемещения   тела? По определению: перемещение — векторная физическая величина — вектор, соединяющий начальную и конечную точку движения. Т.е. для нахождения перемещения необходимо найти модуль вектора перемещения (длину этого вектора) и направление данного вектора. Пометим его на рисунке (рис. 2). Исходя из условий задачи, спортсмен пробежал 10 полных кругов и 0,25 части окружности. Пусть старт произошёл в точке А (выбираем по собственному желанию, ибо в задаче это не конкретизировано), тогда после 10 кругов спортсмен оказался в этой же точке, а после 0,25 круга (четверть окружности) в точке В. Теперь мы видим нашу задачу — найти длину  , по рисунку он является частью прямоугольного треугольника с катетами   и  , и искомой гипотенузой  . Основным способом поиска сторон прямоугольного треугольника является теорема Пифагора. Для нашей задачи:
 (2)

В правой части уравнения известны все параметры, значит, мы можем найти искомые значения.
Считаем: и не забываем о размерностях:

 (м)

---

 (м)
Ответ:   (м),   (м).

Задача 8. Человек прошел по проспекту 240 м, затем повернул на перекрестке и прошел в перпендикулярном направлении еще 70 м. На сколько процентов путь, пройденный человеком, больше модуля его перемещения?
Дано: 

 

 м

 м
Найти: 

 — ?

 

Решение



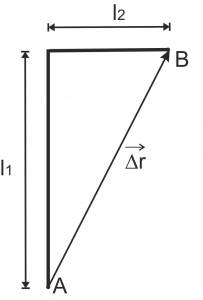
Рис. 1. Путь и перемещение
Думаем: В задаче не заданы буквенно представленные отрезки, давайте определим их:    м,   м. Вопрос задачи относится к траектории движения. Такого типа задачи лучше всего начинать с рисунка (рис. 1). Пусть человек стартует с точки А, проходит расстояние  , а потом поворачивает и приходит в точку В.
Решаем: Разбираемся с найти: по заданию необходимо найти «На сколько процентов путь, пройденный человеком, больше модуля его перемещения», т.е:

% =  % (1)

Тогда наша мини-задачка — это найти путь ( ) и модуль перемещение тела ( ). По определению, путь — скалярная физическая величина, численно равная длине траектории, т.е. для нахождения пути необходимо найти расстояние, пройденное телом за интересующее время движения. В нашем случае, путь состоит из двух отрезков заданных длин, тогда:

---

 (2)

По определению: перемещение — векторная физическая величина — вектор, соединяющий начальную и конечную точку движения. Т.е. для нахождения перемещения необходимо найти модуль вектора перемещения (длину этого вектора) и направление данного вектора. В нашем случае, вектор перемещения — это вектор, соединяющий точки В и А. Модуль этого вектора является частью прямоугольного треугольника, причём, гипотенузой. Для нахождения гипотенузы в таком треугольнике легче использовать теорему Пифагора. Тогда:

 (3)

Подставляем в (1):

% (4)

Справа известно всё, поэтому мы решили задачу.
Считаем: 

% = 19%
Ответ: на  %.

Задача 9. Часовой охраняет объект, огороженный квадратным забором ABCD, обходя его по периметру. Чему будут равны его путь   и перемещение  , если он из точки А, перейдёт в точку B, затем точку С, затем точку D, после чего вернётся в точку А? Длина стороны квадрата  .

Дано:



Найти:

 — ?

 — ?

 

Решение



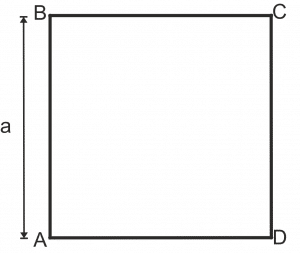
Рис. 1. Траектория и путь

Вопрос задачи относится к траектории

---

 движения. Такого типа задачи лучше всего начинать с рисунка (рис. 1).
Решаем: Обратимся к первому вопросу: чему равен путь   тела? По определению, путь — скалярная физическая величина, численно равная длине траектории, т.е. для нахождения пути необходимо найти расстояние, пройденное телом за интересующее время движения. Исходя из этого определения, наш путь — это расстояние от точки A до до точки B, затем до точки С, далее до точки D и обратно в А, т.е. фактически необходимо найти периметр квадрата, стороной  :

 (1)

Перейдём ко второму вопросу: чему равен модуль перемещения   тела? По определению: перемещение — векторная физическая величина — вектор, соединяющий начальную и конечную точку движения. Т.е. для нахождения перемещения необходимо найти модуль вектора перемещения (длину этого вектора) и направление данного вектора. В нашем случае это вектор, соединяющий начало движения (точка А) и конец движения (точка A). Исходя из определения, модуль перемещения равен нулю, т.к. человек вернулся в начальную точку своего путешествия:

 (2)

Ответ:  ;  .

Задача 10. На озере находится плот массой   кг. На одном краю плота стоит человек массой   кг. Определите расстояние, на которое относительно берега переместится плот, если человек пройдёт по плоту путь   м. В начальный момент скорость плота была равна нулю.

Дано:

---