Файл: Лабораторные Группировка и ее виды. Графическое построение рядов распределений.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 62
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=60+10*6/8=67,5
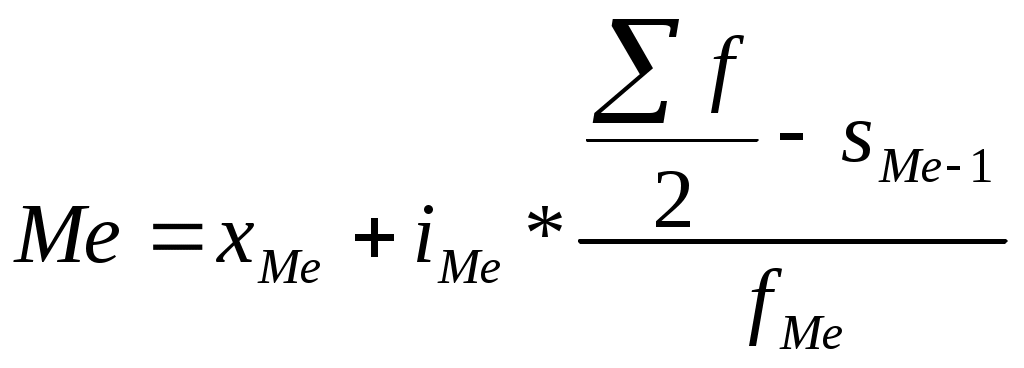 , т.к. 83>65 (130/2), то
, т.к. 83>65 (130/2), тоМе = 70 +10*(65-60)/22=72,27
2) графический метод
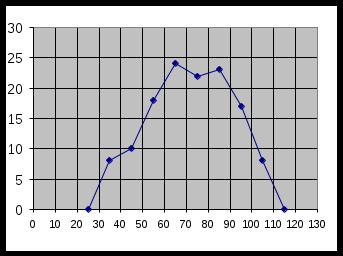
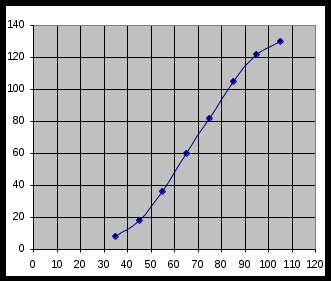
. Показатели вариации
4.1. Супермаркет имеет данные о покупках, совершаемых покупателями за определенный период. Рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности исследуемой совокупности.
| Сумма покупки, тыс.руб. | Количество покупок |
| До 100 | 24 |
| 100 – 200 | 28 |
| 200 – 300 | 40 |
| 300 – 400 | 32 |
| 400 – 500 | 26 |
| 500 – 600 | 19 |
Решение: промежуточные данные удобно представить в таблице
Таблица 4.1.1
Расчет показателей вариации (промежуточные данные)
| x | f | | | | | | |
| До 100 | 24 | 50 | 1200 | 160,95 | 3862,8 | 25904,9 | 621717,7 |
| 100 – 200 | 28 | 150 | 2800 | 60,95 | 1706,6 | 3714,903 | 104017,3 |
| 200 – 300 | 40 | 250 | 6000 | 39,05 | 1562 | 1524,903 | 60996,1 |
| 300 – 400 | 32 | 350 | 8000 | 139,05 | 4449,6 | 19334,9 | 618716,9 |
| 400 – 500 | 26 | 450 | 9100 | 239,05 | 6215,3 | 57144,9 | 1485767 |
| 500 – 600 | 19 | 550 | 8550 | 339,05 | 6441,95 | 114954,9 | 2184143 |
| Итого | 169 | X | 35650 | Х | 24238,25 | 222579,4 | 5075359 |
| Среднее | Х | Х | 210,95 | Х | 143.42 | Х | 30031.71 |
Показатели, характеризующие вариацию
Таблица 4.1.2
Расчет показателей вариации
| Показатель | Формула расчета |
| Размах | |
| Среднее линейное отклонение | 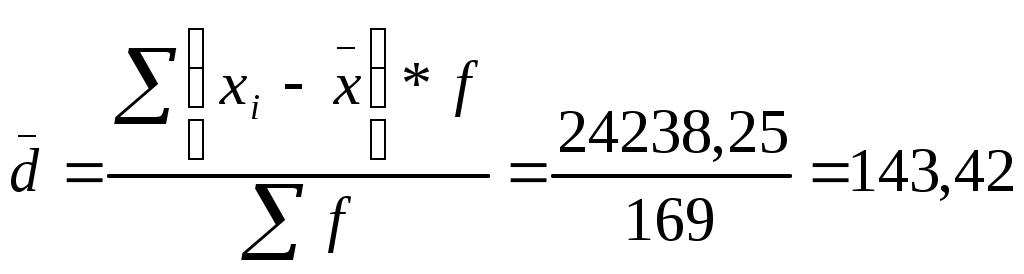 |
| Среднее квадратическое отклонение | 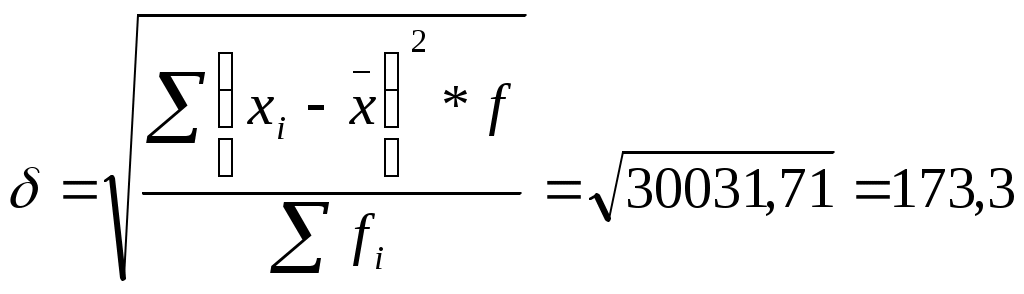 |
| Коэффициент вариации | |
| Коэффициент осцилляции | |
| Линейный коэффициент вариации | 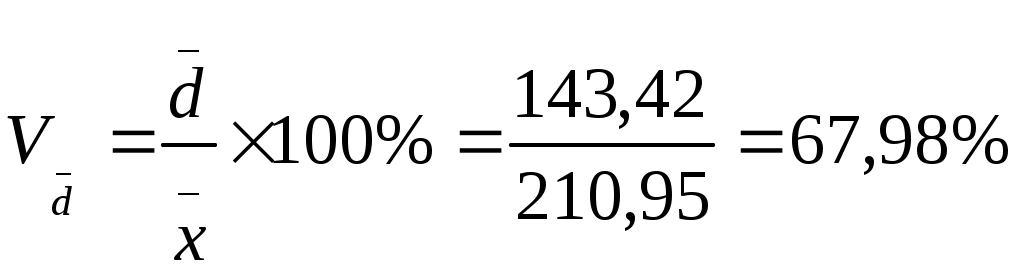 |
5. Выборочное наблюдение
5.1. Из партии в 1 млн.шт. мелкокалиберных патронов путем случайного бесповторного отбора взято для определения дальности боя 1000 шт. По результатам испытаний с вероятностью 0,954 определить для всей партии патронов:
1) возможные пределы средней дальнобойности
2) долю стандартных изделий, если к стандартной продукции относятся патроны с дальностью боя 30- 45 м
| Дальность боя, м | Число патронов |
| 25 | 110 |
| 30 | 175 |
| 35 | 290 |
| 40 | 155 |
| 45 | 120 |
| 50 | 150 |
Решение: 1) представлю промежуточные данные в таблице
Таблица5.1.1
Расчет промежуточных данных для вычисления пределов средней дальнобойности
| x | f | | | | | |
| 25 | 110 | 2750 | 12,25 | 1347,5 | 150,0625 | 16506,88 |
| 30 | 175 | 5250 | 7,25 | 1268,75 | 52,5625 | 9198,438 |
| 35 | 290 | 10150 | 2,25 | 652,5 | 5,0625 | 1468,125 |
| 40 | 155 | 6200 | 2,75 | 426,25 | 7,5625 | 1172,188 |
| 45 | 120 | 5400 | 7,75 | 930 | 60,0625 | 7207,5 |
| 50 | 150 | 7500 | 12,75 | 1912,5 | 162,5625 | 24384,38 |
| Итого | 1000 | 37250 | Х | Х | Х | 59937,5 |
- средняя ошибка выборки. Тогда средняя дальнобойность имеет вид:
37,25-0,49
36,76
2)
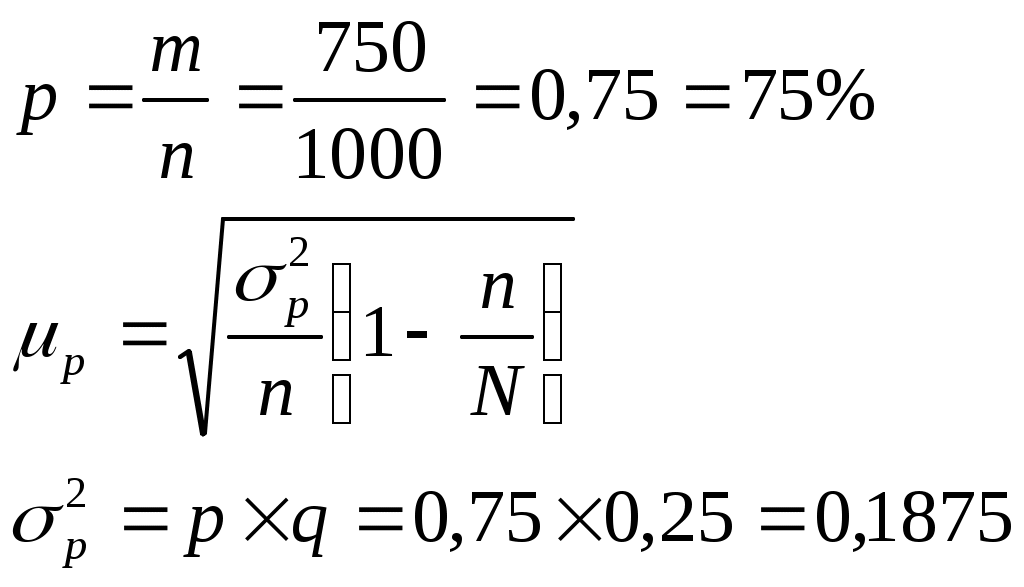
72,26
5.2. Определите сколько электроламп из всей партии изделий следует подвергнуть обследованию в порядке случайной бесповторной выборки, чтобы с вероятностью 0,954 предельная ошибка не превышала 3% среднего веса спирали (средний вес составляет 42 мг). Коэффициент вариации среднего срока службы компьютеров по данным предыдущих обследований составляет 6%, а вся партия состоит из 1220 электроламп.
Решение: запишу условие задачи
x
 =42 мг Формула оптимальной численности выборки для повтор-
=42 мг Формула оптимальной численности выборки для повтор- t=2
N=1220 n =
n - ?
Таким образом необходимо обследовать 16 электроламп
6. Корреляционно-регрессионный анализ
6.1. По исходным данным о предприятиях отрасли, представленным в приложении 3, по группе предприятий (берутся по вариантам, приведенным в табл. 5.6.1) необходимо: