Министерство науки и ВЫСШЕГО ОБРАЗОВАНИЯ Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уральский государственный экономический университет» (УрГЭУ)

ЭКЗАМЕН
по дисциплине

«Высшая математика»

Институт непрерывного и дистанционного образования Направление подготовки 38.03.05 Бизнес-информатика Направленность (профиль) Цифровой бизнес

Студент Группа ИДО ОЗБ БИ-22 СБ Преподаватель Иванов Андрей Николаевич

Екатеринбург

2023 г

1. 
   Условие задачи
   

2. 
   Решение задачи графическим методом
   

Наименование витаминов	Виды биодобавок		Запасы витаминов
	«Телец»	«Овен»
A	16	4		784
B1	8	7		552
E	5	9		567
Прибыль	4000	7200		—

Пусть:

X₁ — кормовая биодобавка «Телец»

X₂ — кормовая биодобавка «Овен»

Составим систему ограничений:

---

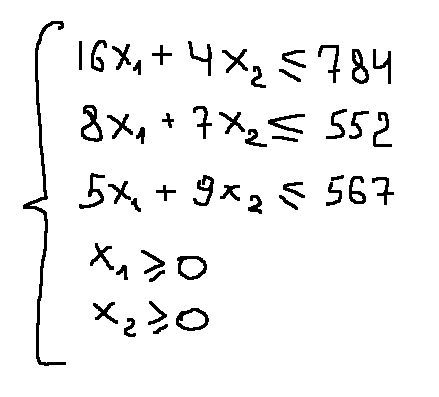
Целевая функция:



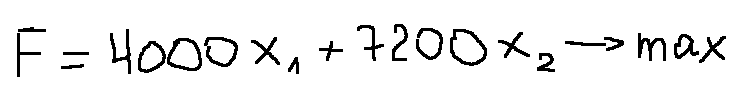
Построим графики функций:

1. 
   16x₁ + 4x₂ = 784
   

Точки	x1	x2
A	0	196
B	49	0

2. 
   8x₁ + 7x₂ = 552
   

Точки	x1	x2
C	0	78,9
D	69	0

3. 
   5x₁ + 9x₂ = 567
   

Точки	x1	x2
E	0	63
F	113,4	0

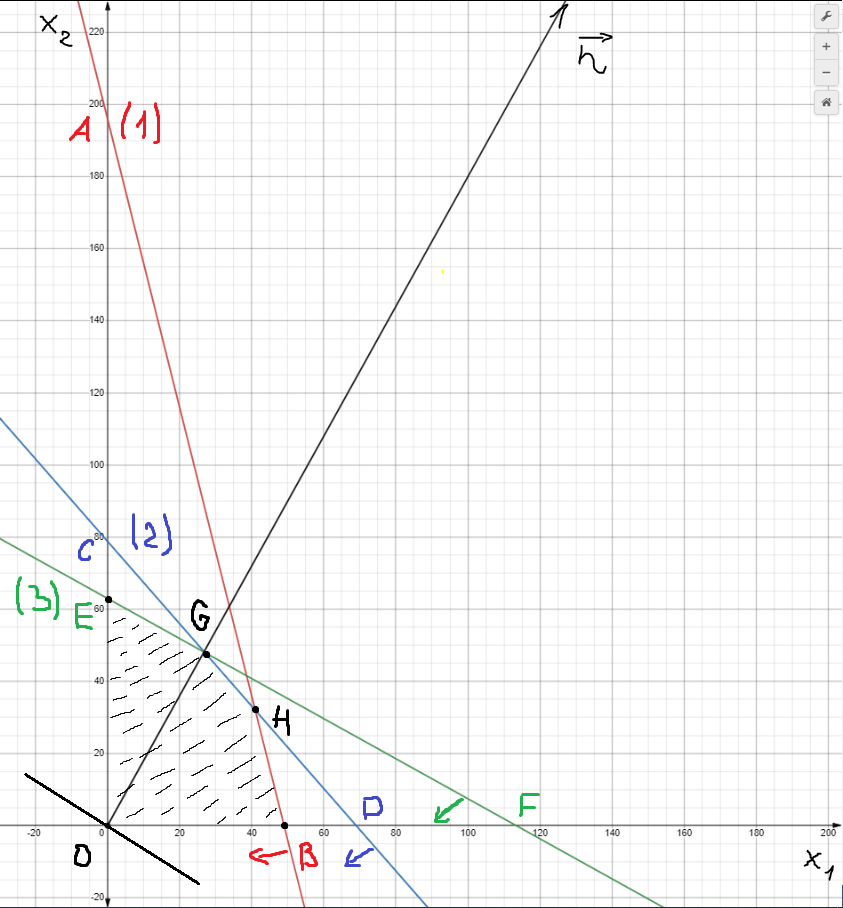
На графике определяем область, удовлетворяющую неравенствам исходя из заданной системы ограничений. Т.к. в системе ограничений по 3-м витаминам A, B₁ и E указано меньше либо равно, то область, удовлетворяющая неравенствам на графике, находится ниже и левее.

Границами допустимых решений является многоугольник EGHBO.

Строим вектор градиента из коэффициентов целевой функции n(4000;7200), а также прямую, перпендикулярную вектору градиента.

Оптимальным решением данной задачи будет являться такое решение, при котором наша целевая функция будет достигать максимума.

Из графика видно, что двигая нашу прямую в направлении вектора градиента, мы получим 2 оптимальных решения нашей задачи – это значение функции в точке G и в точке E.

Вычислим значение функции в каждой из точек.

1. 
   Точка G – это пересечение второй и третьей прямой, уравнение (2) и (3)
   

G = (2) ⋂ (3)

Решим систему уравнений и найдем координаты точки G:



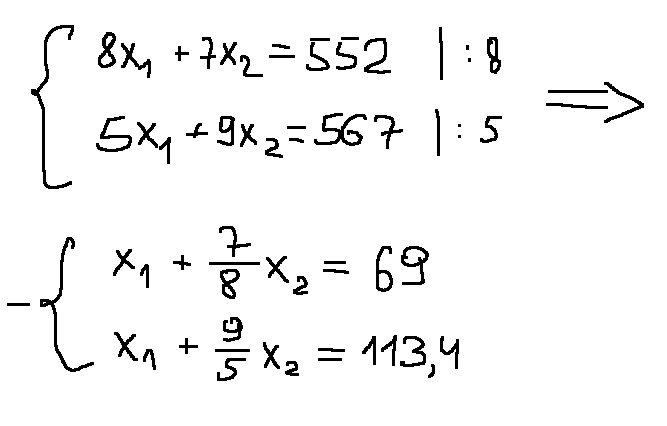
Из второго уравнения вычитаем первое уравнение

---

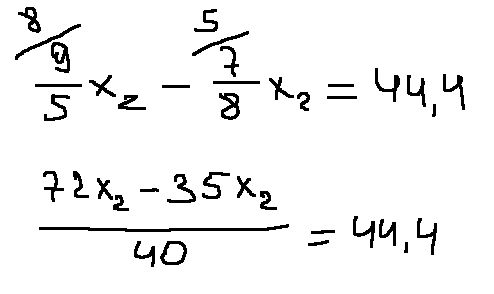
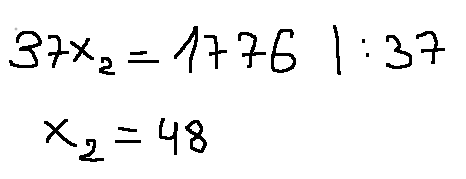
Подставляем х₂ во второе уравнение и находим x₁



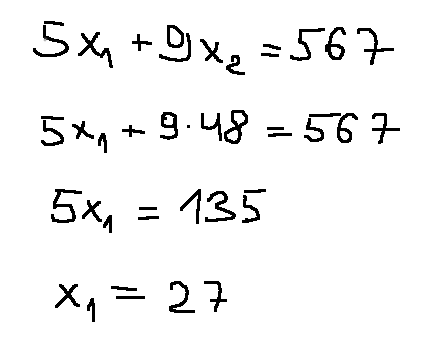
G(x1; x2) = (27; 48)

Подставим полученные значения в целевую функцию:

2. 
   Точка E — перпендикулярная прямая вектора градиента параллельна прямой 3 на отрезке EG, что также является оптимальным решением задачи в точке Е.
   

Для определения координат точки E решим систему уравнений:



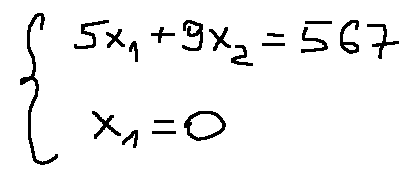
Подставим х₁ в уравнение и найдем х₂



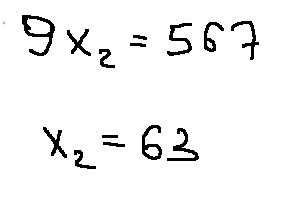
E(x1; x2) = (0; 63)

Подставим полученные значения в целевую функцию:

3. 
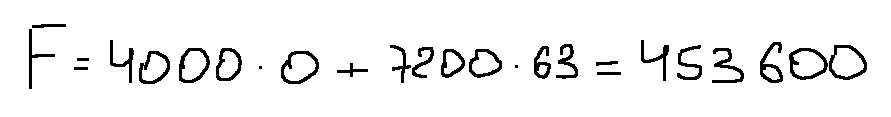
   Ответ задачи
   

Чтобы прибыль достигла максимума и составляла 453600р. (453,6 тыс.р.) необходимо выпускать 27 биодобавок вида «Телец» и 48 биодобавок вида «Овен» либо выпускать только 63 биодобавки вида «Овен».

---

Смотрите также файлы

• Технология приготовления неводных растворов..docx

• Производственной практики (по профилю специальности).docx

• А Аналитический обзор литературы по теме диссертационной работы.docx

• Реабилитация официальное оправдание невинно осуждённых лиц, восстановление их в прежних правах.docx

• Содержание Введение Техническое описание и анализ конструкции системы смазки и суфлирования Техническое обслуживание Расчетная часть Информационные ресурсы Техническое описание и анализ конструкции системы смазки и суфлирования.docx