Добавлен: 24.11.2023
Просмотров: 98
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Особенности надежности и безопасности СЖАТ
2. Показатели надёжности для невосстанавливаемых и восстанавливаемых систем
3. Методы расчета показателей надежности СЖАТ
3.1 Статистические оценки показателей надежности
3.2 Расчет надежности комбинационных схем
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессов
3.6 Расчет эксплуатационной надежности СЖАТ
5. Способы повышения надежности и безопасности устройств и систем ЖАТ
Определим вероятность истинности функции f как сумму вероятностей разрешенных наборов, то есть таких, на которых функция f равна 1:
Pf = ∑Rkf
Pf = R0 + R1 +R5 + R6 + R7
Pf =0,084+0,336+0,224+0,024+0,096=0,764
Определим вероятность функции ошибки как сумму вероятностей, того, что на выходе схемы происходит ошибка при наличии сбоя:
P( ) = ∑Rkf
) = ∑Rkf
P( ) = R1= 0,336
) = R1= 0,336
P( ) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504
) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504
P(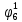 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
P(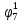 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
P( ) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504
) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504
P( ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
P( ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
P( ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
Вероятность того, что произойдет неисправность, которая приведет к ошибке на выходе схемы:
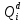 =
= 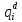 * P(
* P( )
)
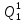 =
=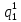 *P(
*P( ) = 0,001*0,336=33,6*10-5
) = 0,001*0,336=33,6*10-5
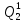 =
=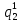 *P(
*P( ) = 0,001*0,504=50,4*10
) = 0,001*0,504=50,4*10
-5
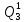 =
=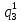 *P(
*P( ) = 0,001*0,644 =64,4*10-5
) = 0,001*0,644 =64,4*10-5
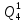 =
=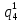 *P(
*P( ) = 0,001*0,644=64,4*10-5
) = 0,001*0,644=64,4*10-5
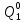 =
=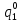 *P(
*P( ) = 0,001*0,504=50,4*10-5
) = 0,001*0,504=50,4*10-5
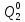 =
=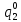 *P(
*P( ) =0,001*0,644=64,4*10-5
) =0,001*0,644=64,4*10-5
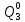 =
=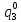 *P(
*P( ) = 0,001*0,644=64,4*10-5
) = 0,001*0,644=64,4*10-5
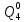 =
=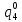 *P(
*P( ) = 0,001*0,644=64,4*10-5
) = 0,001*0,644=64,4*10-5
Вероятность ошибки на выходе схемы в момент времени t определяется по следующей формуле:
Q = ∑
Q = 45,6*10-4
Вероятность отсутствия ошибки на выходе схемы, то есть вероятность исправной работы равна:
P = 1-Q = 1 – 45,6*10-4 = 0,99544
В разделе по заданной функции алгебры логики была построена комбинационная схема, после чего была рассчитана ее надежность. Вероятность ошибки на выходе схемы в момент времени t равна 45,6*10-4, вероятность исправной работы схемы - 0,99544.
Исходные данные
Вариант № 18
λik=λ=18*10-4 1/ч.
μik=μ=0,55 1/ч.
РАСЧЕТЫ
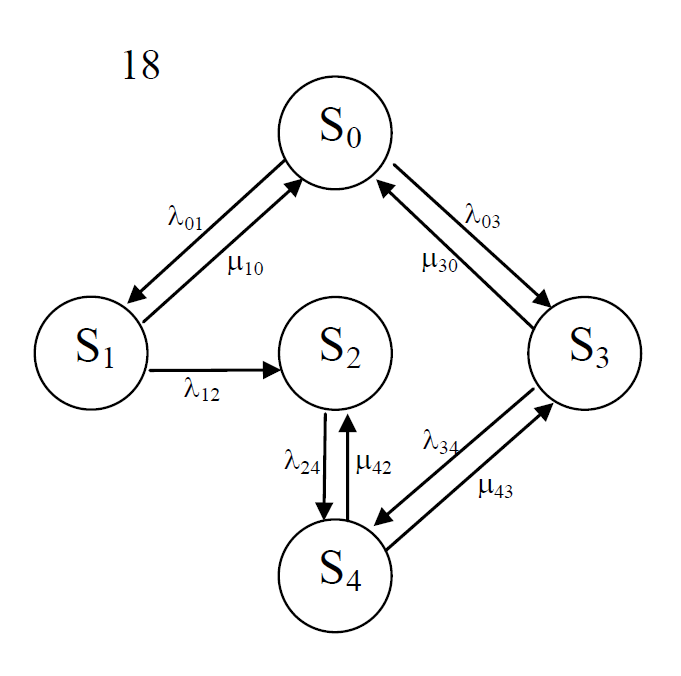
Рисунок 5. Граф состояний схемы.
Исходя из графа, система может находиться в одном из четырех состояний:
0 – исправное состояние;
1 – первое работоспособное состояние, отказал первый элемент, второй и третий – исправны;
2 – второе работоспособное состояние, отказал второй элемент, первый и третий – исправны;
3 – третье работоспособное состояние, отказал третий, первый и второй – исправны;
4 – неработоспособное состояние, отказали последовательно три элемента и находятся в состоянии ремонта.
Составим систему уравнений Колмогорова для финальных вероятностей нахождения во всех состояниях.



Система состоит из шести уравнений, пять неизвестных, значит можно путем подстановки выразить каждую переменную:
Р0=0,355
P1=0,131
P2=0,487
P3=0,025
P4=0,002
Вероятность отказа системы:
QC=P4=0,00018
Вероятность безотказной работы:
PC=1-QC=1-0,00018=0,99982
Время наработки на отказ:
Tср=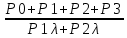 =
=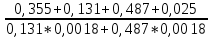 =897,1 ч.
=897,1 ч.
Интенсивность отказов:
λc=1/ Tср=1/897,1 = 0,00111 1/ч.
Среднее время восстановления:
Tв=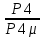 =
=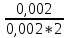 =0,5
=0,5
Коэффициент готовности:
Кг=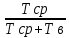 =
=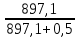 =0,999
=0,999
Для нахождения среднего времени безотказной работы выполним преобразование Лапласа для уравнений Колмогорова с учетом начальных условий:
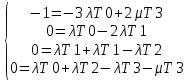 →
→ 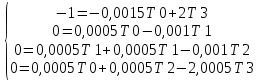
Система состоит из четырех уравнений, 3 неизвестных, значит можно путем подстановки выразить каждую переменную:
T0=1333 ч.
T1=666 ч.
T2=666 ч.
T3=0,5 ч.
Среднее время безотказной работы системы:
Tот=T0+T1+T2+T3=1333+666+666+0,5=2665,5 ч.
3.4 Структурный метод расчета надежности
Исходные данные
Вариант № 10
1 Узел: (n1*n2) v (n3*(n4 v n5))
2 Узел: n6
3 Узел: n7 v n8 v n9
λ1=18*10-51/ч.
λ2=18*10-51/ч.
λ3=18*10-51/ч.
λ4=18*10-51/ч.
λ5=18*10-51/ч.
λ6=18*10-51/ч.
λ7=18*10-51/ч.
λ8=18*10-51/ч.
λ9=18*10-51/ч.
Тву1= 18 ч.
Тву2= 18 ч.
Тву3=18 ч.
t =1 год = 8760 ч
РАСЧЕТЫ
Логическая функция схемы:

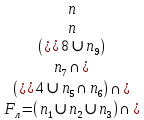
Арифметическая функция:
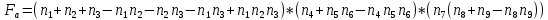
Преобразуем узлы схемы:

Рис.8.
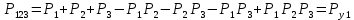
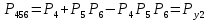
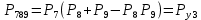
Функция надежности:
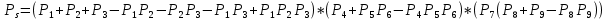
Значения функции надёжности схемы за t=1 год (8760 ч):
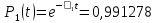
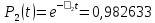
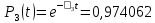
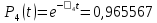
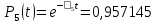
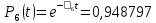
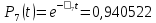
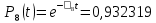
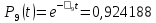
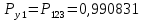
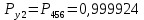
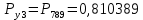
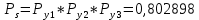
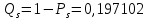
Интенсивностьотказов:
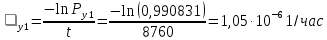
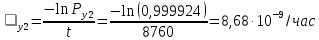
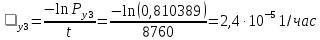
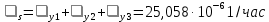
Среднее время наработки до отказа:
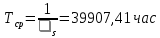
Среднее время восстановления системы:
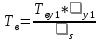 +
+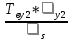 +
+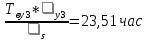
Коэффициент готовности:
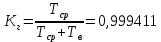
Вывод: после определения всех параметров системы можно сделать вывод, что система в течении года будет работать надёжно с вероятностью 80,2898%
3.5 Топологический метод расчета надежности резервированных систем
На рис. 1 приведена структурная схема некоторой системы с восстановлением. Значения интенсивности отказа и времени восстановления каждого элемента, вид и кратность резервирования, а также число ремонтных бригад заданы в соответствии с вариантом (табл.1).
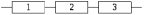
Рис. 1. Структурная схема системы
Необходимо построить систему с резервированием и найти выигрыш надёжности по времени наработки на отказ: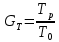 , где
, где 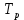 - время наработки на отказ для резервированной системы,
- время наработки на отказ для резервированной системы, 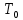 - время наработки на отказ для нерезервированной системы.
- время наработки на отказ для нерезервированной системы.
Pf = ∑Rkf
Pf = R0 + R1 +R5 + R6 + R7
Pf =0,084+0,336+0,224+0,024+0,096=0,764
Определим вероятность функции ошибки как сумму вероятностей, того, что на выходе схемы происходит ошибка при наличии сбоя:
P(
 ) = ∑Rkf
) = ∑RkfP(
 ) = R1= 0,336
) = R1= 0,336 P(
 ) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504
) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504P(
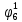 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644P(
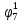 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644P(
 ) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504
) = R2 + R3 +R5+ R6 +R7= 0,036 + 0,144 +0,224+0,024+0,096= 0,504P(
 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644P(
 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644P(
 ) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644
) = R0 + R2 + R3 + R4 +R5+ R6 +R7= 0,084+0,036 + 0,144 + 0,056 +0,224+0,024+0,096= 0,644Вероятность того, что произойдет неисправность, которая приведет к ошибке на выходе схемы:
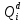 =
= 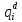 * P(
* P( )
)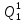 =
=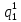 *P(
*P( ) = 0,001*0,336=33,6*10-5
) = 0,001*0,336=33,6*10-5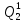 =
=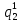 *P(
*P( ) = 0,001*0,504=50,4*10
) = 0,001*0,504=50,4*10
-5
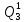 =
=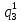 *P(
*P( ) = 0,001*0,644 =64,4*10-5
) = 0,001*0,644 =64,4*10-5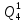 =
=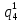 *P(
*P( ) = 0,001*0,644=64,4*10-5
) = 0,001*0,644=64,4*10-5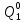 =
=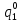 *P(
*P( ) = 0,001*0,504=50,4*10-5
) = 0,001*0,504=50,4*10-5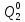 =
=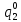 *P(
*P( ) =0,001*0,644=64,4*10-5
) =0,001*0,644=64,4*10-5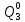 =
=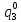 *P(
*P( ) = 0,001*0,644=64,4*10-5
) = 0,001*0,644=64,4*10-5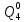 =
=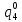 *P(
*P( ) = 0,001*0,644=64,4*10-5
) = 0,001*0,644=64,4*10-5Вероятность ошибки на выходе схемы в момент времени t определяется по следующей формуле:
Q = ∑

Q = 45,6*10-4
Вероятность отсутствия ошибки на выходе схемы, то есть вероятность исправной работы равна:
P = 1-Q = 1 – 45,6*10-4 = 0,99544
В разделе по заданной функции алгебры логики была построена комбинационная схема, после чего была рассчитана ее надежность. Вероятность ошибки на выходе схемы в момент времени t равна 45,6*10-4, вероятность исправной работы схемы - 0,99544.
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессов
Исходные данные
Вариант № 18
λik=λ=18*10-4 1/ч.
μik=μ=0,55 1/ч.
РАСЧЕТЫ

Рисунок 5. Граф состояний схемы.
Исходя из графа, система может находиться в одном из четырех состояний:
0 – исправное состояние;
1 – первое работоспособное состояние, отказал первый элемент, второй и третий – исправны;
2 – второе работоспособное состояние, отказал второй элемент, первый и третий – исправны;
3 – третье работоспособное состояние, отказал третий, первый и второй – исправны;
4 – неработоспособное состояние, отказали последовательно три элемента и находятся в состоянии ремонта.
Составим систему уравнений Колмогорова для финальных вероятностей нахождения во всех состояниях.



Система состоит из шести уравнений, пять неизвестных, значит можно путем подстановки выразить каждую переменную:
Р0=0,355
P1=0,131
P2=0,487
P3=0,025
P4=0,002
Вероятность отказа системы:
QC=P4=0,00018
Вероятность безотказной работы:
PC=1-QC=1-0,00018=0,99982
Время наработки на отказ:
Tср=
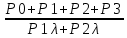 =
=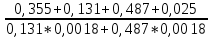 =897,1 ч.
=897,1 ч.Интенсивность отказов:
λc=1/ Tср=1/897,1 = 0,00111 1/ч.
Среднее время восстановления:
Tв=
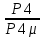 =
=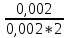 =0,5
=0,5Коэффициент готовности:
Кг=
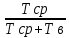 =
=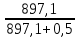 =0,999
=0,999
Для нахождения среднего времени безотказной работы выполним преобразование Лапласа для уравнений Колмогорова с учетом начальных условий:
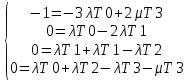 →
→ 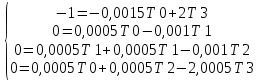
Система состоит из четырех уравнений, 3 неизвестных, значит можно путем подстановки выразить каждую переменную:
T0=1333 ч.
T1=666 ч.
T2=666 ч.
T3=0,5 ч.
Среднее время безотказной работы системы:
Tот=T0+T1+T2+T3=1333+666+666+0,5=2665,5 ч.
3.4 Структурный метод расчета надежности
Исходные данные
Вариант № 10
1 Узел: (n1*n2) v (n3*(n4 v n5))
2 Узел: n6
3 Узел: n7 v n8 v n9
λ1=18*10-51/ч.
λ2=18*10-51/ч.
λ3=18*10-51/ч.
λ4=18*10-51/ч.
λ5=18*10-51/ч.
λ6=18*10-51/ч.
λ7=18*10-51/ч.
λ8=18*10-51/ч.
λ9=18*10-51/ч.
Тву1= 18 ч.
Тву2= 18 ч.
Тву3=18 ч.
t =1 год = 8760 ч
РАСЧЕТЫ
Логическая функция схемы:

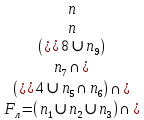
Арифметическая функция:
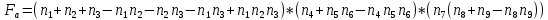
Преобразуем узлы схемы:

Рис.8.
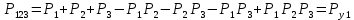
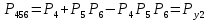
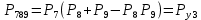
Функция надежности:
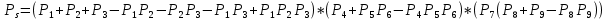
Значения функции надёжности схемы за t=1 год (8760 ч):
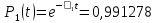
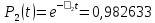
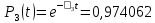
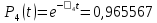
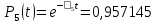
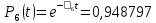
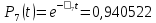
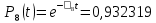
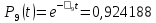
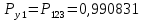
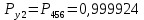
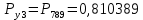
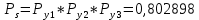
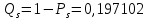
Интенсивностьотказов:
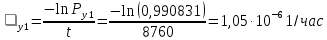
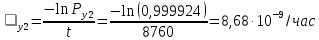
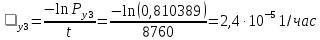
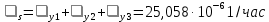
Среднее время наработки до отказа:
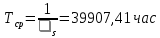
Среднее время восстановления системы:
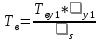 +
+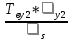 +
+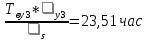
Коэффициент готовности:
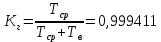
Вывод: после определения всех параметров системы можно сделать вывод, что система в течении года будет работать надёжно с вероятностью 80,2898%
3.5 Топологический метод расчета надежности резервированных систем
На рис. 1 приведена структурная схема некоторой системы с восстановлением. Значения интенсивности отказа и времени восстановления каждого элемента, вид и кратность резервирования, а также число ремонтных бригад заданы в соответствии с вариантом (табл.1).
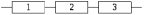
Рис. 1. Структурная схема системы
Необходимо построить систему с резервированием и найти выигрыш надёжности по времени наработки на отказ:
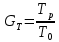 , где
, где 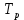 - время наработки на отказ для резервированной системы,
- время наработки на отказ для резервированной системы, 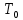 - время наработки на отказ для нерезервированной системы.
- время наработки на отказ для нерезервированной системы.