Файл: Курсовой проект по учебному курсу Теория механизмов и машин.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 24.11.2023

Просмотров: 158

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М инистерство науки и высшего образования Российской Федерациифедеральное государственное бюджетное образовательное учреждениевысшего профессионального образования«Тольяттинский государственный университет»КУРСОВАЯ РАБОТА (КУРСОВОЙ ПРОЕКТ) по учебному курсу «Теория механизмов и машин»

Студент
Леонтьева В.А

(И.О. Фамилия)



Группа
ТБбп-1902б

(И.О. Фамилия)



Преподаватель

Балахнина А.А.

(И.О. Фамилия)


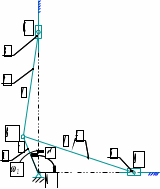
Тольятти 20221. Синтез и кинематическое исследование механизма1.1. Исходные данныеДана схема (рис. 1), частота вращения ведущего звена nAB = 1900 об/мин и длины звеньев rAB = 65 мм, lBC = 260 мм, lBD = 170 мм, φ =30град.Рис. 1. Схема механизма1.2. Описание построения плана механизмаПринимаю длину кривошипа 1 на чертеже равной 40 мм.Расчет масштабного коэффициента производим по формуле

,
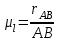(1.1)
где μl – масштабный коэффициент, м/мм;rАВ – длина кривошипа по заданию, м;AB – длина кривошипа на чертеже, мм. 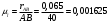.Расчет длин звеньев механизма на чертеже ведем, используя следующую формулу

,
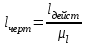(1.2)
где lчерт – длина звена на чертеже, мм;lдейст – действительная длина звена, м;
μl – масштабный коэффициент, м/мм. 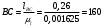; 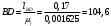.1.3. Структурный анализ механизмаСоставим описание звеньев и кинематических пар механизма и занесём их соответственно в таблицу 1.1 и таблицу 1.2.Таблица 1.1Характеристика звеньев механизма

Обозначение звена
Описание звена

0
стойка

1
кривошип

2
шатун

3
ползун

4
шатун

5
ползун
Таблица 1.2Характеристика кинематических пар механизма

Обозначение

пары
Подвижность пары
Звенья,

образующие пару
Тип

А0-1
одноподвижная
стойка, кривошип
низшая вращательная

В1-2
одноподвижная
кривошип, шатун

низшая вращательная

В1-4
одноподвижная
кривошип, шатун
низшая вращательная

С2-3
одноподвижная
ползун, шатун
низшая вращательная

С0-3
одноподвижная
ползун, стойка
низшая поступательная

D4-5
одноподвижная
ползун, шатун
низшая вращательная

D0-5
одноподвижная
ползун, стойка
низшая поступательная
Степень свободы плоского механизма находится по формуле Чебышева

,
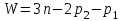(1.3)
где n – число подвижных звеньев, в данном механизме их 5 (табл. 1.1);p1 – число одноподвижных кинематических пар 5 класса, в данном механизме их 7 (табл. 1.2);p2 – количество двухподвижных пар 4 класса, в данном механизме их нет (табл. 1.2). 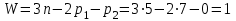.1.4. Построение кинематических диаграммПо найденным на планах механизма положениям ведомого звена 5 вычерчиваем график перемещения ползуна D, начиная от крайнего нижнего положения.Время оборота ведущего звена (кривошипа AВ) найдем по формуле

,
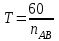(1.4)
где Т – время оборота кривошипа АВ, с;nAB – частота вращения кривошипа АВ, об/мин. 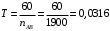.Изобразим это время на оси абсцисс отрезком x = 180 мм. Масштабный коэффициент времени на диаграмме рассчитывается по формуле

,
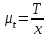(1.5)
где μt – масштабный коэффициент времени на диаграмме, с/мм;Т – время оборота кривошипа АВ, с;х – принятая длина отрезка по оси абцисс, мм. 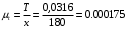.Масштаб перемещений на диаграмме, откладываемых по оси ординат, принимаем равным величине удвоенного масштаба длины на схеме механизма.Масштабный коэффициент угла поворота кривошипа найдем по формуле

,
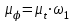(1.6)
где μφ – масштабный коэффициент угла поворота кривошипа, рад/мм;mt – масштабный коэффициент времени на диаграмме, м/мм;w1 – угловая скорость звена 1, рад/с;Угловую скорость звена 1 можно найти по следующей формуле

,
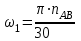(1.7)
где w1 – угловая скорость звена 1, рад/с;nAB – частота вращения кривошипа АВ, об/мин. 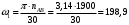.Тогда 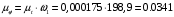.Дифференцируя график перемещений, получим график изменения скорости ведомого звена. Дифференцирование проводим графически методом хорд.Вычисляем масштабный коэффициент скорости на диаграмме

,
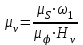(1.8)
где mv – масштабный коэффициент скорости на диаграмме, м·с-1/мм;ms – масштабный коэффициент перемещений на диаграмме, м/мм;w1 – угловая скорость звена 1, рад/с;μφ – масштабный коэффициент угла поворота кривошипа, рад/мм;Hv – полюсное расстояние, мм.Полюсное расстояние Hv принимаю равным 25 мм.Тогда 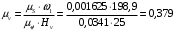.Аналогичным способом получим кривую ускорения, дифференцируя график скорости.Вычисляем масштабный коэффициент ускорения на диаграмме

,
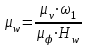(1.9)
где mw – масштабный коэффициент ускорения на диаграмме, м·с-2/мм;mv – масштабный коэффициент скорости на диаграмме, м·с-1/мм;w1 – угловая скорость звена 1, рад/с;μφ – масштабный коэффициент угла поворота кривошипа, рад/мм;Hv – полюсное расстояние, мм. 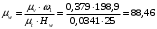.1.5. Описание построения плана скоростейОт произвольно взятой точки Р отложим вектор скорости 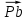, который направлен перпендикулярно кривошипу в направлении 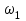. Принимаем длину вектора 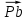на плане скоростей равной 70 мм.Вращение кривошипа задано схемой механизма и направлено против часовой стрелки.
Скорость точки B кривошипа можно найти, предварительно рассчитав угловую скорость вращения кривошипа

,
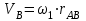(1.10)
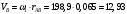
где VB – скорость точки В кривошипа, м/с;ω1 – угловая скорость звена 1, рад/с;rАВ – длина кривошипа по заданию, м.Расчет масштабного коэффициента скорости

,
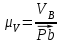(1.11)
где μV – масштабный коэффициент скорости, м·с-1/мм;VB – скорость точки В кривошипа, м/с;Pb – длина вектора Pb на плане скоростей, мм. 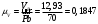.Для каждого из 12-и положений:Скорость точки C ползуна найдем, решив совместно два векторных уравнения
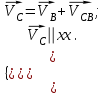(1.12)
Первое уравнение описывает движение т. С относительно т. В, а второе описывает движение т. С, принадлежащей ползуну.Скорость точки D ползуна найдем, решив совместно два векторных уравнения
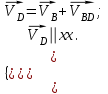(1.13)
Первое уравнение описывает движение т. D относительно т. В, а второе описывает движение т. D, принадлежащей ползуну.Векторы скоросте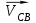й и 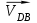строим из т. B перпендикулярно шатунам 2 и 4 до их пересечения с осью xx.1.6 Описание построения плана ускоренийОт полюса Π отложим вектор нормального ускорения в направлении от В к А в виде вектора

Смотрите также файлы