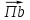.

Нормальное (центростремительное) ускорение т. В кривошипа найдем по формуле

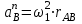(1.14)

где aⁿ_B – нормальное ускорение т. В, м/с²;

ω₁ – угловая скорость звена 1, рад/с;

r_АВ – длина кривошипа по заданию, м

.

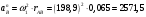Принимаем длину вектора .

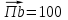
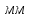Расчет масштабного коэффициента ускорения проведем по формуле

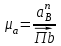(1.15)

где μ_a – масштабный коэффициент ускорения, м·с^-2/мм;

aⁿ_B – нормальное ускорение т. В, м/с²;

Πb – длина вектора Πb на плане скоростей, мм.

.

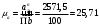Для каждого из 2-ух положений:

Ускорение точки C найдем, решив совместно два векторных уравнения

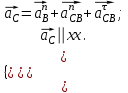(1.16)

Ускорение точки D найдем, решив совместно два векторных уравнения

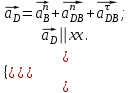(1.17)

Нормальные ускорения 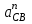и 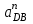строим параллельно шатунам 2 и 4 соответственно, причем они направлены от т. С и D к т. В.

Тангенциальные ускорения 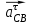и 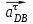строим перпендикулярно нормальным ускорениям 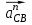и 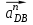из конца векторов до пересечения с осью xx.

---

Для «0-го» положения:

Нормальное ускорение определим по формуле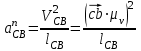

,

(1.18)

где aⁿ_CB – нормальное ускорение звена CB, м/с²;

cb – длина вектора cb скорости шатуна СВ на чертеже, мм;

l_CB – действительная длина шатуна CB, м.

;

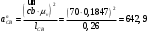На плане ускорений длина вектора n_cb будет равна

,

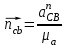(1.19)

где n_cb – длина вектора нормального ускорения точки B кривошипа, мм;

aⁿ_CB – нормальное ускорение звена CB, м/с²;

μ_a – масштабный коэффициент ускорения, м·с^-2/мм.

.

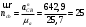Нормальное ускорение найдем по формуле (1.18)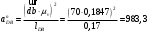

.

А длину вектора n_db по формуле (1.19)

.

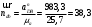Для «2-го» положения:

Нормальное ускорение определим по формуле (1.18)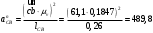

;

На плане ускорений длина вектора n_cb будет равна (1.19)

.

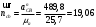Нормальное ускорение найдем по формуле (1.18)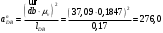

.

А длину вектора n_db по формуле (1.19)

.

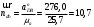Тангенциальное ускорение звена СВ находим из плана ускорений по формуле

,

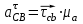(1.20)

где a^τ_CB – тангенциальное ускорение звена CB, м/с²;

τ_СВ

---

– величина вектора τ_СВ на плане ускорений;

μ_a – масштабный коэффициент ускорения, м·с^-2/мм.

;

.
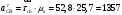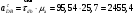1.7 Сравнительный анализ скоростей и ускорений

№ позиции	1	2	3	4	5
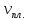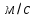	8,64	13,46	12,93	8,92	4,28
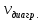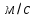	8,40	12,90	12,75	8,70	4,20
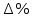	2,82	4,19	1,38	2,48	1,94

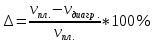
№ позиции	0	11
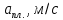2	3828	2883,6
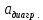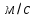, 2	3729	2885
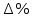	2,65	0,05

2. Синтез кулачкового механизма
2.1. Исходные данные и схема механизма

Дана схема кулачкового механизма (рис. 2), угол удаления φ_у = 104º, угол дальнего стояния φ_д = 20º, угол возврата φ_в = 104º, минимальный угол передачи движения γ_min = 60º и подъем толкателя h = 40 мм = 0,04 м. Направление вращения кулачка против часовой стрелки.

Тип кулачкового механизма – I

---

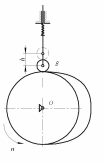
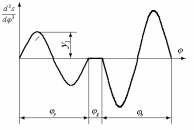
Рис. 2. Схема кулачкового механизма
2.2. Построение диаграммы

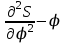
На оси абсцисс φ откладываем углы φ_У, φ_Д, φ_Вв масштабе 2º/1мм.

Масштабный коэффициент угла поворота найдем по формуле

,

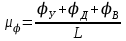(2.1)

где μ_j – масштабный коэффициент, рад/мм;

φ_У – угол удаления, рад;

φ_Д – угол дальнего стояния, рад;

φ_В – угол возврата, рад;

L– длина отрезка на чертеже, мм.

.

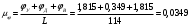Длину отрезка ОР находим по формуле

,

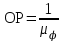(2.2)

где OP – длина отрезка OP на чертеже, мм;

μ_j – масштабный коэффициент, рад/мм.

.

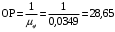Высоту кривой принимаем равной y₁ = 50 мм.

Разбиваем угол удаления и угол возврата на диаграмме на 10 равных частей.

Масштабный коэффициент .
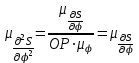2.3. Построение диаграммы .

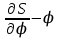Диаграмма 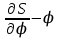получается графическим интегрированием диаграммы аналогов ускорений 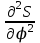. Для этого:

1. 
   разбиваем угол удаления на 12 равных частей 01; 12; 23; ...;
   
2. 
   из середины каждой части проведем перпендикуляр до пересечения с кривой ;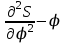
   

3. 
   соединим полюс P с проекциями середин частей кривой на ось ;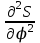
   
4. 
   на диаграмме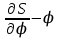 откладываем отрезки параллельные соответствующим отрезкам, полученным в предыдущем подпункте.
   

Все построения ведем в масштабном коэффициенте

---

.


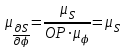2.4. Построение диаграммы .

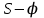Диаграмму 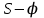построим, графически проинтегрировав диаграмму аналогов скоростей 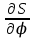аналогично пункту 2.3.

Замеряем наибольшую величину S_max на чертеже, S_max = 27,9 мм.

Масштабный коэффициент 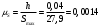м/мм.
2.5. Определение минимального радиуса кулачка.

Берем на плоскости произвольную т. О, откладываем от неё отрезок ОА, равный ходу h толкателя. Этот отрезок размечаем в соответствии с диаграммой 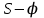. Через точки деления проводим перпендикуляры к линии ОА. От точек деления на перпендикулярах откладываем влево при подъеме и вправо при опускании толкателя отрезки, взятые из графика . Эти отрезки нужно откладывать в том масштабе, в котором отложен отрезок ОА, т.е. в масштабе 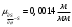. Соединяем плавной кривой концы этих отрезков и получаем кривую 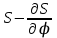. Проводим под углом 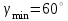к горизонтали две касательные к построенной кривой. Эти прямые образуют в итоге область, в которой может располагаться центр кулачка. Выбираю длину отрезка BО равной r₀ = 60 мм на чертеже. Следовательно, минимальный теоретический радиус кулачка будет равен

,

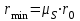(2.3)

где r_min – минимальный теоретический радиус кулачка, м;

μ_S – масштабный коэффициент, м/мм;

r₀ – минимальный радиус кулачка на чертеже, мм.

.


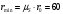2.6. Профилирование кулачка

Построения ведем в масштабе м/мм. Проведём окружность радиусом BA, полученным в предыдущем пункте. В произвольном месте окружности ОВ₀ выберем точку отсчета – т. В

---

Смотрите также файлы

• Баллов 0,80 из 1,00.docx

• Бекітемін Мектеп директоры Ж. К. Кабашева 2017ж Келісемін.docx

• лгерімі тмен оушылармен жргізілетін жмыс Аылшын тілі.doc

• Музыкальные инструменты.docx

• Налогу на доходы физических лиц.docx