Туынды көмегімен функцияны зерттеу

 

 

1. Функцияның өсуі мен кемуі

 

Туындының қосымшаларының бірі оның функцияны зерттеуді, оның графигін салуда қолдану болып табылады. Функцияның өсуі мен кемуінің қажетті және жеткілікті шарттарын тұжырымдайық.

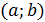
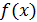
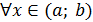
Теорема 1. (қажетті шарт). Егер   интервалында дифференциалданатын    функциясы өсетін (кемитін) болса, онда    үшін   ( ).

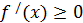
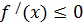
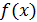
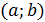
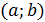
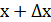
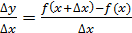
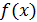
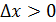
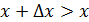
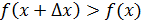
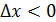
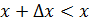
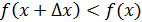
Д/уі.   функциясы    интервалында өсетін болсын.   интервалынан х және   кез-келген нүктелерін алайық және   қатынасын қарастырайық.   функциясы өседі, сондықтан да   болса,  онда   және  ; егер   болса, онда   және  . Екі жағдайда да, 

---

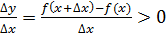
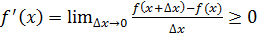
, себебі бөлшектің алымы мен бөлімі бірдей таңбалы. Теорема шарты бойынша   функциясының х нүктесінде туындысы бар және қарастырылатын, қатынастың шегі болып табылады. Сәйкесінше,  .   функциясы   интервалында кемитін жағдайда осылай қарастырылады.

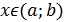
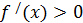
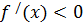
Теорема 2. (жеткілікті шарт). Егер   функциясы   үшін   интервалында дифференциалданса және   ( ) болса, онда осы функция (a; b) интервалында өседі (кемиді).

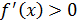
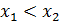
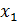
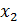
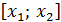
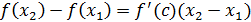
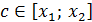
Д/уі.   болсын.    интервалында   болатындай   және   нүктелерін алайық.   кесіндісінде Лагранж  теоремасы қолданылады:  , мұндағы . Шарт бойынша, 

---

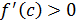
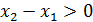
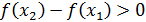
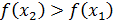
,  . Сәйкесінше,    немесе  , яғни    функциясы   интервалында өседі.

Өспелі және кемімелі функциялар монотонды функциялар деп аталады.

 

 

2. Функцияның максимумы мен минимумы

 

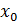
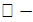
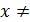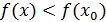
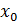
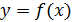
Егер   нүктесінің  маңайы бар болып, осы маңайдың барлық  x₀ үшін   теңсіздігі орындалса,   нүктесі   функциясының максимум нүктесі деп аталады. Функцияның минимум нүктесі де осылай анықталады: егер

 

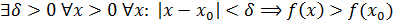
(9.1)

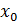
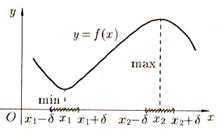
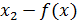
болса,   функциясының минимум нүктесі. 9.1-суретте   -минимум нүктесі,  -функциясының максимум нүктесі

 

	9.1–сурет–  -min нүктесі,   - функциясының max нүктесі

---

 

Максимум (минимум) нүктедегі функция мәні функцияның максимум (минимумы) деп аталады. Функцияның максимумы (минимумы) функцияның экстремумы деп аталады.

Теорема 3. (экстремумның қажетті шарты). Егер    дифференциалданатын функциясының   нүктесінде экстремумы бар болса, оның осы нүктедегі туындысы нөлге тең: f ^/(x₀)=0.

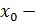
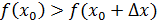
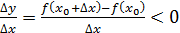
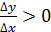
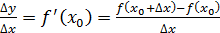
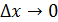
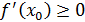
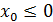
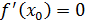
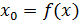
Д/уі.   максимум нүкте болсын делік. Яғни,   нүктесінің маңайында   теңсіздігі орындалады. Олай болса,   болғанда  , ал    болғанда,  . Теорема шарты бойынша   туындысы бар болады.   болғанда шекке көшу арқылы   аламыз, егер    және  , егер   болса. Сондықтан,  . Егер   функциясының минимум нүктесі болса, 3- теоремасының тұжырымдамасы осылай дәлелденеді.

---

           теңдігінің геометриялық мағынасы   дифференциалданатын функциясының экстремум нүктесінде, оның графигіне жүргізілген жанама Ox осіне параллель.

Үзіліссіз функцияның тек туындысы нөлге немесе туындысы болмайтын нүктелерінде ғана экстремумы болады. Осындай нүктелерді  деп атайды.

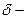
Теорема 4. (экстремумның жеткілікті шарты). Егер   функциясы   күдікті нүктесінің қандай да  маңайында дифференциалданатын болса, және одан өткенде (солдан оңға)  f ^/(x₀) туындысы плюстен минусқа ауысса,  - максимум нүкте, минустан плюске  -минимум нүктесі

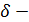
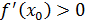
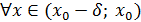
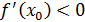
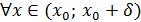
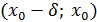
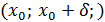
Д/уі. нүктесінің  маңайын қарастырайық.     және  ,   шарттары орындалсын делік. Сонда   функциясы   интервалында өседі, ал   интервалында кемиді. Бұдан, 

---

Смотрите также файлы

• Доклад на тему биография Ивана Сергеевича Тургенева.docx

• Идея научной философии в позитивизме.docx

• Семинар 2 с примерами решения задач по логике к теме Понятие (часть 2).docx

• Аттестация прокурорских работников.pptx

• Лица, участвующие в деле и другие участники процесса как субъекты гражданских процессуальных правоотношений.doc