Файл: Туынды кмегімен функцияны зерттеу Функцияны суі мен кемуі.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 42
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
функциясының  нүктесіндегі мәні
нүктесіндегі мәні 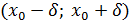 интервалындағы ең үлкен болатындығы шығады, яғни барлық
интервалындағы ең үлкен болатындығы шығады, яғни барлық 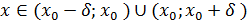 үшін
үшін 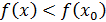 болады. Бұл
болады. Бұл  функциясының максимум нүктесі болатындығын білдіреді.
функциясының максимум нүктесі болатындығын білдіреді.
Функцияны экстремумға зерттеу оның барлық экстремумдарын табу деген сөз. Функцияны экстремумға зерттеудің келесі ережелері шығады:
1) функциясының күдікті нүктелерін табу;
функциясының күдікті нүктелерін табу;
2) олардың ішінен тек анықталу облысының кіретін ішкі нүктелерді таңдап алу;
3) таңдалған әрбір күдікті нүктелердің әрқайсысының оң жағынан және сол жағынан f /(x) туындысының таңбасын зерттеу;
4) 4. теоремасына (экстремумның жеткілікті шарты) сәйкес экстремум нүктелерді (егер олар бар болса) жазып алу және олардағы функция мәнін есептеу.
Теорема 5. Егер нүктесінде
нүктесінде  функциясының бірінші туындысы нөлге тең (f /(x0)=0)), ал
функциясының бірінші туындысы нөлге тең (f /(x0)=0)), ал  нүктесіндегі екінші туындысы бар болса, және нөлге тең болмаса, онда f //(x0)<0 болғанда
нүктесіндегі екінші туындысы бар болса, және нөлге тең болмаса, онда f //(x0)<0 болғанда 
нүктесінде функция максимумға ие, ал f //(x0)>0 болғанда минимумға ие
Д/уі.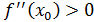 болсын делік.
болсын делік. 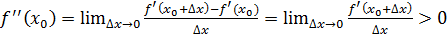 болғандықтан,
болғандықтан,  нүктесінің аз маңайында
нүктесінің аз маңайында 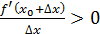 болады. Егер
болады. Егер  болса, онда
болса, онда 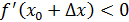 ; егер
; егер  болса, онда
болса, онда 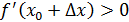 болады. Осылайша,
болады. Осылайша,  нүктесі арқылы өткенде бірінші туындының таңбасы минустан плюске өзгереді. Сәйкесінше,
нүктесі арқылы өткенде бірінші туындының таңбасы минустан плюске өзгереді. Сәйкесінше,  минимум нүкте. Егер
минимум нүкте. Егер 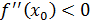 болса, онда
болса, онда  нүктесінде функция максимумға ие болатындығы осылайша дәлелденеді.
нүктесінде функция максимумға ие болатындығы осылайша дәлелденеді.
3. Функцияның кесіндідегі ең үлкен және ең кіші мәні
 функциясы
функциясы 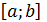 кесіндісінде үзіліссіз болсын. Мұндай функция өзінің ең үлкен және ең кіші мәнін қабылдайды және олар не
кесіндісінде үзіліссіз болсын. Мұндай функция өзінің ең үлкен және ең кіші мәнін қабылдайды және олар не 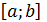 кесіндісінің ішкі нүктесінде, не кесіндінің ұштарында, яғни
кесіндісінің ішкі нүктесінде, не кесіндінің ұштарында, яғни 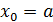 не
не 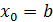
болғанда. Егер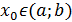 болса, онда
болса, онда  нүктесін берілген функцияның күдікті нүктелерінен іздек керек.
нүктесін берілген функцияның күдікті нүктелерінен іздек керек.
 кесіндісінде функцияның ең үлкен, ең кіші мәндерін табудың келесі ережесін аламыз:
кесіндісінде функцияның ең үлкен, ең кіші мәндерін табудың келесі ережесін аламыз:
1) -да функцияның ең үлкен, ең кіші мәндерін табудың келесі ережелерін аламыз;
-да функцияның ең үлкен, ең кіші мәндерін табудың келесі ережелерін аламыз;
2) табылған күдікті нүктелердегі функцияның мәнін есептеу;
3) кесінді ұштарында, яғни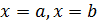 нүктелеріндегі функция мәнін есептеу;
нүктелеріндегі функция мәнін есептеу;
4) барлық табылған мәндер ішінен ең үлкені мен ең кішісін таңдау.
4 .Функция графигінің дөңестігі, иілу нүктелері
Егер дифференциалданатын функциясының графигі оған жүргізілген кез-келген жанамадан жоғары болса, онда график – төменнен дөңес деп, егер жанамадан төмен болса, график – жоғарыдан дөңес деп аталады.
дифференциалданатын функциясының графигі оған жүргізілген кез-келген жанамадан жоғары болса, онда график – төменнен дөңес деп, егер жанамадан төмен болса, график – жоғарыдан дөңес деп аталады.
Үзіліссіз функциясының дөңестігі әртүрлі бөліктерін ажыратып тұратын нүкте–иілу нүктесі деп аталады. 9.3–суретте
функциясының дөңестігі әртүрлі бөліктерін ажыратып тұратын нүкте–иілу нүктесі деп аталады. 9.3–суретте  қисығы
қисығы 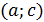 интервалында жоғарыдан ойыс,
интервалында жоғарыдан ойыс, 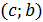 интервалында төменнен ойыс, ал
интервалында төменнен ойыс, ал 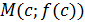 –иілу нүктесі.
–иілу нүктесі.
Жоғарыдан және төменнен ойыс интервалдар келесі теореманың көмегімен табылады.
Теорема 5. Егер функциясының
функциясының  интервалының барлық нүктесінде екінші туындысы теріс, яғни f //(x)<0 болса, онда осы интервалда функция графигі жоғарыдан дөңес. Егер f //(x)>0,
интервалының барлық нүктесінде екінші туындысы теріс, яғни f //(x)<0 болса, онда осы интервалда функция графигі жоғарыдан дөңес. Егер f //(x)>0, 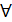 x
x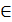 (a; b) болса, функция графигі төменнен дөңес.
(a; b) болса, функция графигі төменнен дөңес.
Д/уі: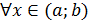 үшін
үшін 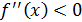 болсын. Функция графигінен абциссасы:
болсын. Функция графигінен абциссасы: 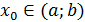 болатын кез-келген нүктені алып, М арқылы жанама жүргізейік. Функция графигі жанамадан төмен орналасқанын көрсетейік. Ол үшін
болатын кез-келген нүктені алып, М арқылы жанама жүргізейік. Функция графигі жанамадан төмен орналасқанын көрсетейік. Ол үшін 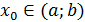 нүктесінде
нүктесінде  қисығының
қисығының 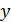 ординатасымен
ординатасымен 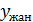 салыстырайық. Біз білетіндей, жанаманың теңдеуі мына түрде болады:
салыстырайық. Біз білетіндей, жанаманың теңдеуі мына түрде болады:
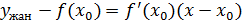 , яғни
, яғни 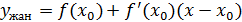 . Лагранж теоремасы бойынша
. Лагранж теоремасы бойынша 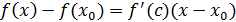 , мұнда c
, мұнда c  және
және 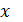 нүктелерінің арасында жатыр. Сондықтан,
нүктелерінің арасында жатыр. Сондықтан,
яғни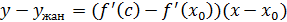 .
. 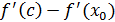 айырманы тағы да Лагранж формуласы бойынша түрлендірелік:
айырманы тағы да Лагранж формуласы бойынша түрлендірелік:
мұнда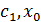 және с арасында жатыр.
және с арасында жатыр.
Осылайша,
Осы теңдікті зерттейміз:
1) егер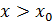 , онда
, онда 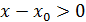 ,
, 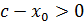 және
және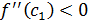 . Демек
. Демек 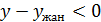 , яғни
, яғни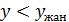 ;
;
2) егер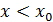 , онда
, онда 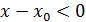 ,
, 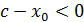 және
және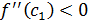 . Демек
. Демек 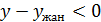 , яғни
, яғни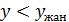 .
.
Сонымен, интервалының барлық нүктелерінде жанаманың ординатасы графиктің ординатасынан үлкен екендігі дәлелденді, яғни функция графигі жоғарыға дөңес. Осыған ұқсас,
интервалының барлық нүктелерінде жанаманың ординатасы графиктің ординатасынан үлкен екендігі дәлелденді, яғни функция графигі жоғарыға дөңес. Осыған ұқсас,
| | 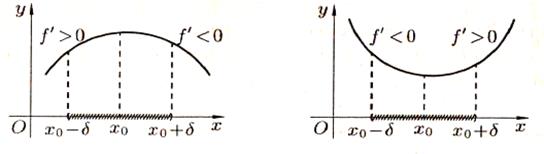 | |
| | 9.2-сурет- | |
Функцияны экстремумға зерттеу оның барлық экстремумдарын табу деген сөз. Функцияны экстремумға зерттеудің келесі ережелері шығады:
1)
2) олардың ішінен тек анықталу облысының кіретін ішкі нүктелерді таңдап алу;
3) таңдалған әрбір күдікті нүктелердің әрқайсысының оң жағынан және сол жағынан f /(x) туындысының таңбасын зерттеу;
4) 4. теоремасына (экстремумның жеткілікті шарты) сәйкес экстремум нүктелерді (егер олар бар болса) жазып алу және олардағы функция мәнін есептеу.
Теорема 5. Егер
нүктесінде функция максимумға ие, ал f //(x0)>0 болғанда минимумға ие
Д/уі.
3. Функцияның кесіндідегі ең үлкен және ең кіші мәні
болғанда. Егер
1)
2) табылған күдікті нүктелердегі функцияның мәнін есептеу;
3) кесінді ұштарында, яғни
4) барлық табылған мәндер ішінен ең үлкені мен ең кішісін таңдау.
4 .Функция графигінің дөңестігі, иілу нүктелері
Егер
Үзіліссіз
| | 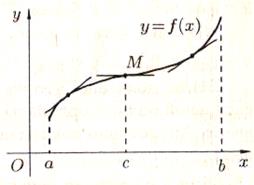 | |
| | 9.3-сурет. М нүктесі иілу нүктесі | |
Жоғарыдан және төменнен ойыс интервалдар келесі теореманың көмегімен табылады.
Теорема 5. Егер
Д/уі:
| | | |
яғни
| | | |
мұнда
Осылайша,
| | | |
Осы теңдікті зерттейміз:
1) егер
2) егер
Сонымен,