болғанда графиктің төменге дөңестігі дәлелденеді. Функцияның графигінің иілу нүктелерін табу үшін келесі теорема қолданылады.

Теорема 6. (иілу нүктелерінің бар болуының жеткілікті шарты). Егер   екінші ретті туынды x₀ нүктесі арқылы өткен де, таңбасын өзгертсе, онда графиктің абсцисссасы    болатын графиктің нүктесі иілу нүктесі болады. 

 

 

5 .Функция графигінің асимптотасы

 

Егер функцияның асимптоталарына білсек, онда оның графигін салу жеңіл болады. Асимптота ұғымы гиперболаның формуларын зертегенде  қарастырылған. Еске түсіріп өтелік. Қисықтың асимптотасы деп координатаның бас нүктесінен бастап қисық бойынан әртүрлі жолмен бөліп алғандағы нүктеден түзуге дейінгі арақашықтық нөльге ұмтылатын, түзуді айтамыз (9.3-суретті қара). Асимптоталар тік, көлденең, көлбеу болады.

 

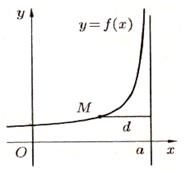	9.4-сурет. х=а түзуі y=f(x) функциясының асимптотасы

 

 түзуі   функциясының графигінің тік асимптотасы деп аталады, егер    немесе    немесе  .

 

 

6. Функцияны зерттеудің жалпы схемасы және графигін салу

 

 функциясын  зерттеуді белгілі тізбек бойынша жүргізу қажет.

---

1. Функцияның анықталу облысын табу;

2. Графиктің координаталар осімен қиылысу нүктелерін табу (мүмкін болса);

3. Функцияның таңбасы тұрақты интервалдарын табу (f(x)>0 немесе  f(x)<0  болатындай аралықтарды табу);

4. Функцияның жұп, тақ, не жалпы түрдегі болатындығын анықтау;

5. Функция графигінің асимптоталарын табу;

6. Функцияның монотондық интервалдарын табу;

7. Функцияның экстремумдарын табу;

8. Функция графигінің ойыс интервалдары мен иілу нүктелерін табу;

Жүргізілген зерттеу негізінде функция графигін салу қарапайым функциялар үшін  1, 2, 7 операцияларды орындау жеткілікті. Егер барлық 8 операцияны орындаған соң да функция графигі аса түсінікті болмаса, онда функцияны периодтылыққа зерттеп, қосымша бірнеше нүктелерді салып функцияның басқа қасиеттерін зерттеу керек. Кейде зерттеу жүргізе отырып, функция графигін салу тиімді.0>0>0>

---

Смотрите также файлы

• Доклад на тему биография Ивана Сергеевича Тургенева.docx

• Идея научной философии в позитивизме.docx

• Семинар 2 с примерами решения задач по логике к теме Понятие (часть 2).docx

• Аттестация прокурорских работников.pptx

• Лица, участвующие в деле и другие участники процесса как субъекты гражданских процессуальных правоотношений.doc