Файл: Лабораторная работа 1 Математическое моделирование экономических процессов с помощью парных регрессионных моделей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 45
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Доверительные интервалы для коэффициентов регрессии β1 и β0имеют соответственно вид:
;
.
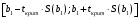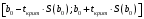Если окажется, что доверительный интервал включает 0, то соответствующий коэффициент регрессии объявляется незначимым.
При заданном уровне значимости = 0,05 и числе степеней свободы, равном n – 2, где n – заданный объем выборки (у нас n = 10) критическое значение статистики Стьюдента tкрит = 2,306.
Теперь строим доверительные интервалы для β1 и β0 соответственно:
;
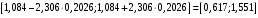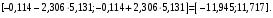
Поскольку интервал коэффициента β1 не включает нулевое значение, а интервал коэффициента β0 включает, делаем вывод о значимом отличии от нуля коэффициента β1 и не значимом коэффициента β0.
8. Интервал для прогноза среднего значения зависимой переменной при значении объясняющей переменной x* (точнее, прогноза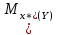
) по линейному уравнению регрессии имеет вид:
,
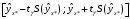где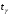
находят по таблицам критических точек распределения Стьюдента для заданных значений и числа степеней свободы v = n – 2 (в случае парной регрессии). Мы уже знаем, что при 
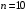и 
(т.е.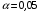
) 
.
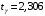Вычисляем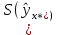
с учетом полученных ранее результатов:
.
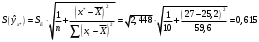Из выборочного уравнения прямой регрессии имеем:
.
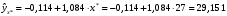Получаем окончательный вид искомого доверительного интервала:
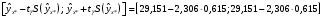
или
.
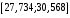Для расчета доверительного интервала возможных индивидуальных значений наблюдений при значении объясняющей переменной
x*применяется формула:
,
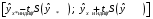где
.
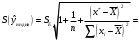
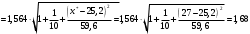Окончательно получаем:
.
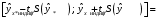
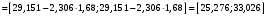ЛИТЕРАТУРА
Доверительные интервалы для коэффициентов регрессии β1 и β0имеют соответственно вид:
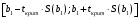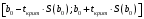; .Если окажется, что доверительный интервал включает 0, то соответствующий коэффициент регрессии объявляется незначимым.
При заданном уровне значимости = 0,05 и числе степеней свободы, равном n – 2, где n – заданный объем выборки (у нас n = 10) критическое значение статистики Стьюдента tкрит = 2,306.
Теперь строим доверительные интервалы для β1 и β0 соответственно:
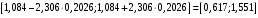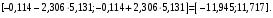
; Поскольку интервал коэффициента β1 не включает нулевое значение, а интервал коэффициента β0 включает, делаем вывод о значимом отличии от нуля коэффициента β1 и не значимом коэффициента β0.
8. Интервал для прогноза среднего значения зависимой переменной при значении объясняющей переменной x* (точнее, прогноза
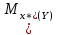) по линейному уравнению регрессии имеет вид: 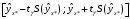,где
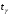находят по таблицам критических точек распределения Стьюдента для заданных значений и числа степеней свободы v = n – 2 (в случае парной регрессии). Мы уже знаем, что при 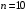и (т.е.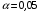 ) 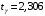.Вычисляем
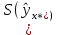с учетом полученных ранее результатов: 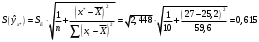.Из выборочного уравнения прямой регрессии имеем:
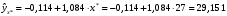.Получаем окончательный вид искомого доверительного интервала:
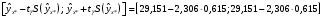
или
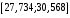.Для расчета доверительного интервала возможных индивидуальных значений наблюдений при значении объясняющей переменной
x*применяется формула:
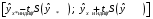,где
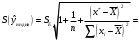
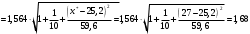.Окончательно получаем:
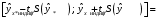
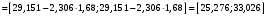.ЛИТЕРАТУРА
-
Бабешко Л.О. Основы эконометрического моделирования. – М.: КомКнига, 2006. – 432 с. -
Бородич С.А. Эконометрика: Учебное пособие. – Мн., Новое знание, 2002. – 408 с. -
Доугерти К. Введение в эконометрику. – М., 2003, – 402 с. -
Елисеева И.И. Практикум по эконометрике. – М.: «Финансы и статистика» – 2007. – 344 с. -
Елисеева И.И. Эконометрика. – М.: «Финансы и статистика» – 2011. – 288 с. -
Магнус Я.Р. и др. Эконометрика. Начальный курс. – М., Дело, 2000. – 400 с. -
Тихомиров Н.П, Дорохина Е.Ю. Эконометрика. – М., Экзамен, 2003. – 512 с.