Файл: Целые и рациональные числа.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.11.2023

Просмотров: 91

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Тема: Первые следствия из теорем Цели: 1) повторить аксиомы стереометрии и применение их при решении задач домашнего задания;2) научить применять следствия из аксиом при решении задач, а также закрепить умение применять аксиомы стереометрии при решении задач;3) формировать умения работать в группе.Ход урока:I. Организационный моментII. Изучение нового материалаРассмотрим и докажем следствия из аксиом. Два следствия есть в учебнике , их будут изучать первая и вторая группа. А потом докажут у доски. Третье следствие «Через две параллельные прямые можно провести плоскость и притом только одну» будет доказывать третья группа самостоятельно.Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.Учащиеся записывают формулировку в тетради и, отвечая на вопросы учителя, делают соответствующие записи и рисунки в тетрадь.- Что дано в теореме? (прямая и не лежащая на ней точка)- Что надо доказать? (проходит плоскость; одна)- Что можно использовать для доказательства? (аксиомы стереометрии)- Какая из аксиом позволяет построить плоскость? (А1, через три точки проходит плоскость и притом только одна)- Что есть в данной теореме и чего не хватает для использования А1 (имеем – точку; необходимы – еще две точки)- Где построим еще две точки? (на данной прямой)- Какой вывод можем сделать? ( через три точки строим плоскость)- Принадлежит ли данной плоскости прямая? ( да)- На основании чего можно сделать такой вывод? ( на основании А2: если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости)- Сколько плоскостей можно провести через данные прямую и данную точку? (одну)- Почему? (так как плоскость, проходящая через прямую и плоскость, проходит через данную точку и две точки на прямой, значит по А1 эта плоскость – единственная)Теорема 2. Через две пересекающиеся прямые проходит плоскость и притом только одна.Учащиеся доказывают теорему самостоятельно, затем прослушиваются несколько доказательств и делаются дополнения и уточнения (если они необходимы)Обратить внимание на то, что доказательство опирается не на аксиомы, а на следствие 1.Теорема 3. Доказывает представитель от третьей группы учащихся.III. Закрепление изученного материалаУчащиеся решают задачи № 7, 10, 14 из учебного пособия, делая соответствующие рисунки и записи на доске и в тетрадях.IV. Подведение итогов:- Сформулируйте аксиомы стереометрии.- Сформулируйте следствия из аксиом.Домашнее задание : п.3, №7Математика 10 класс Дата ___________Тема: Параллельные прямые в пространстве Цели: 1) Формирование знаний учащихся определения параллельных прямых в пространстве, теоремы о единственности прямой, параллельной данной, свойств параллельных прямых;2) развитие аналитического мышления; формирование умений выделять главное и обобщать3) развитие познавательного интереса к геометрии в пространстве.Ход урока:I. Организационный моментII. Изучение нового материала1) Вспомним планиметрию.-Каким может быть взаимное расположение двух прямых на плоскости? (Совпадают, пересекаются, параллельны)-Какие прямые в планиметрии называются параллельными?-Перед вами модель куба -Что вы можете сказать о прямых АВ и CD? (Они лежат в одной плоскости, они не пересекаются, параллельны)- Являются ли параллельными прямые В1С и С1С, а AD1 и A1D? (нет, они лежат в одной плоскости, но пересекаются)-Что вы можете сказать о прямых B1C и A1D? Проблема.- Лежат ли они в одной плоскости?(Они лежат в одной плоскости, они параллельны)-Сделайте вывод, какие прямые в пространстве называются параллельными?-Вернёмся к модели куба -Что вы можете сказать о прямых ВС и АА1? (Они не лежат в одной плоскости, не пересекаются и не параллельны)Такие прямые называются скрещивающимися.Запись в тетрадь: «Две прямые называются скрещивающимися, если они не лежат в одной плоскости».2) Являются ли параллельными следующие прямые? Ответ пояснить (слайды №10-11).3) Делаем вывод о взаимном расположении прямых в пространстве (слайд №12).4) Докажем теорему о параллельных прямых (слайды №13-14).5) Учащиеся самостоятельно формулируют определение параллельных отрезков и лучей (слайд №15).III. Решение задачРешение у доски с комментариями.Задача № 17 (слайд №16).Дано:М - середина BD; N - середина CD; Q - середина АС;Р - середина АВ; AD = 12 см; ВС = 14 см.Найти: PMNQP - ?Решение:1. MN || BC (по составу средней линии) ⇒ MN || PQ; PQ || BC.2. РМ || AD (по составу средней линии) ⇒ PM || QN; NQ || DA.Значит, MNQP - параллелограмм (по определению) .3. PQ = 7; РМ = 6 ⇒ PMNQP = 2(7 + 6) = 26 (см).Ответ: 26 см.IV. Подведение итогов урока.- Всегда ли две непересекающиеся прямые в пространстве параллельны?- Какие две прямые в пространстве называются параллельными?- Сколько можно провести в пространстве прямых, проходящих через любую точку пространства, параллельных данной прямой?Домашнее задание П. 4, теорема, задачи № 16, 18(а)Математика 10 класс Урок №16 Дата ___________Тема: Параллельность трех прямых Цели: 1) Рассмотреть взаимное расположение двух прямых в пространстве, теорему о параллельности трех прямых, ввести понятие параллельных прямых в пространстве, сформировать умения применять полученных знания при решении задач.2) Развивать память, логическое мышление, внимание, умение грамотно излагать собственные мысли, умение применять полученные знания.3) Воспитывать аккуратность, старательность, ответственность, дисциплинированность, любовь к предметуХод урока Организационный момент Актуализация опорных знаний учащихся 1. Какие прямые на плоскости называются параллельными?2. Как называются углы, образованные при пересечении параллельных прямых секущей? Изучение нового материала Определение. Две прямые в пространстве называются параллельными, если они не пересекаются и лежат в одной плоскости. Используя рисунок, назовите параллельные прямые. Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. Задача 1. Вершина Q параллелограмма MNPQ лежит в плоскости α, а точки M, N, и P не лежат в этой плоскости. Докажите, что прямые NM и NP пересекают плоскость α.Доказательство. Прямая PQ пересекаетплоскость α в точке Q, так как Q ϵ α, поэтому, согласно лемме о пересечении плоскости параллельными прямыми, прямая NM, параллельная PQ, также пересекает плоскость α. Прямая MQ пересекает плоскость α в точке Q, поэтому параллельная ей прямая NP также пересекает плоскость α, что и требовалось доказать.Теорема. Если две прямые параллельны третьей прямой, то они параллельны.(рассмотреть доказательство теоремы в учебнике стр. 11) Решение задач Задача 1. Докажите, что если плоскость проходит через прямую, которая параллельна второй плоскости, и пересекает эту плоскость, то прямая пересечения параллельна данной прямой. К доске вызывается ученик и доказывает задачу с наименьшей помощью со стороны учителя. После того как задача у доски доказана, учитель показывает, как можно было записать доказательство. Обсуждение. Задача 2. Докажите, что если две плоскости пересекаются,параллельные одной и той же прямой, то прямая пересечения этих плоскостей параллельна данной прямой. . Сначала рисунок к задаче и доказательство обсуждается с  классом. Затем учащиеся записывают доказательство. После того, как задача решена, учитель показывает, как можно было записать доказательство. Решить № 26 Сторона АС треугольника АВС параллельна плоскости a , а стороны АВ и ВС пересекаются с этой плоскостью в точках М и N. Докажите, что треугольники АВС и МВN подобны. Слайд 11Перед решением данной задачи необходимо вспомнить признаки подобия треугольников. Доказательство1. По утверждению 1° : МN || АC. Тогда угол А = углу ВМN (как односторонние при параллельных прямых).2. угол В - общий.З. Таким образом, по двум углам треугольник АВС подобен треугольнику МВN.К доске вызывается ученик и доказывает задачу с помощью учителя. После того как задача у доски доказана, учитель показывает, как можно было записать доказательство. Обсуждение. Слайд 12. Подведение итогов 1) Сформулируйте признак параллельности прямой и плоскости.2) Сформулируйте утверждение, обратное признаки параллельности прямой и плоскости. Правильное ли оно?Домашнее задание№ 27, № 30, № 31Математика 10 класс Урок №17 Дата ___________Тема: Параллельность прямой и плоскостиЦели: 1) Ввести понятия параллельности прямой и плоскости; 2) Воспитывать аккуратность, старательность, ответственность, дисциплинированность, любовь к предмету3) Сформировать представления учащихся об аксиомах стереометрии, взаимном расположении прямой и плоскости, плоскостей в пространстве, способах задания плоскости в пространстве.Ход урока Организационный момент Изучение нового материала Начать с рассмотрения взаимного расположения прямой и плоскости в пространствеВ каком случае прямая и плоскость параллельны (рис. 1. а, б, в)? Прямая и плоскость называются параллельными, если они не имеют общих точек. Показать на предметах обстановки классной комнаты прямые, параллельные плоскости пола.На модели куба (рис. 2) укажите плоскости, параллельные прямой DC, прямой DD1. Как установить параллельность прямой и плоскости?Обратите внимание на модель куба. DC || (AA1B1). В плоскости (AA1B1) имеется прямая АВ || DC; DC || (A1B1C1). В плоскости (А1В1С1) имеется прямая D1C1 || DC. Сделайте предположение. Наличие в плоскости α прямой b || а является признаком, по которому можно сделать вывод о параллельности прямой а и плоскости α.Теорема:Дано: а, α; а ∉ α; b ∈ α; а || b (рис. 3).Доказать, что а || α. Доказательство: По условию b ∈ α; b || а.Предположим, что а ∩ α, тогда по лемме о пересечении плоскости параллельными прямыми прямая b ∩ α, но это невозможно, так как b ∈ α. Следовательно, а ∩ α, поэтому а || α и теорема доказана.Докажем два утверждения, которыми будем пользоваться при решении задач.1. Если плоскость проходит через данную прямую, параллельную другой плоскости и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.Дано:   (рис. 4)Доказать: а || b. Доказательство: По условию   значит, а || b, так как  2. Если одна из 2-х параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.Дано: а || b; а; а || α (рис. 5).Доказать: 1) b || α. 2) b ∈ α. Доказательство: По условию а || b и α || а, следовательно, по лемме о пересечении плоскости параллельными прямыми   то есть b || α или b ∈ α. Решение задач № 18(б), № 20, 22 Подведение итогов Домашнее задание № 18 (a), 19, 21.Математика 10 класс Урок №18 Дата ___________Тема: Параллельность прямой и плоскостиЦели: 1) Закрепить и углубить знания и умения применять теоремы о параллельности прямых, прямой и плоскости при решении задач; подготовить учащихся к контрольной работе и зачету по данной теме. 2) Развивать пространственное воображение учащихся при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание;3) Воспитывать у учащихся ответственное отношение к учебному труду, волю;Ход урока Организационный момент Устная работа. 1. Верна ли формулировка признака параллельности прямой и плоскости: «Прямая, параллельная какой-либо прямой на плоскости, параллельна и самой плоскости». (Нет, прямая может лежать в плоскости).2. Прямые а и b параллельны. Какое положение может занимать прямая а относительно плоскости, проходящей через прямую b?3. Даны прямая и две пересекающихся плоскости. Охарактеризовать все возможные случаи их взаимного расположения. Решение задач по теме урока. Задача № 22Дано: A ∈ α, В ∈ α, С ∈ α; AM = МС; BN = NC.Доказать: MN || α.Доказательство: MN || АВ (по свойству средней линии), АВ ∈ α; MN || α по признаку.Перед решением задачи № 26 дать понятие отрезка, параллельного плоскости.«Отрезок параллелен плоскости, если прямая, содержащая этот отрезок, параллельна плоскости».Задача № 26Дано: АС || α, АВ ∩ α = М; СВ ∩ α = N (рис. 1).Доказать: ΔАВС ΔMBN. Доказательство:1. Докажем, что AC || MN; (по определению).2. Так как АС || MN ⇒ ΔАВС

Тема: Скрещивающиеся прямыеЦели: 1) ввести понятие скрещивающихся прямых; сформулировать и доказать признак скрещивающихся прямых; рассмотреть возможные случаи взаимного расположения прямых в пространстве; 2) развивать логическое и пространственное мышление, развивать владение математической речью; умения делать выводы, обобщать и конкретизировать. 3) воспитывать умение работать в коллективе; воспитывать познавательную активность, самостоятельность, стремление расширять свой кругозор; Ход урока Организационный момент Актуализация опорных знаний учащихся 1. Две прямые в пространстве называются параллельными, если они не пересекаются.2. Прямая а пересекает плоскость α и а║b.Тогда прямая b не пересекает плоскость α.3. Прямая и плоскость называются параллельными, если они не имеют общих точек.4. Прямая а║b, а b ║с. Тогда а ∩с. Изучение нового материала. Б еседа учителя и учащихся попараллелепипеду, по взаимномурасположению прямых.-Являются ли параллельными прямые АА1и DD1; AA1 и CC1? Почему?-Являются ли АА1 и DC параллельными?Они пересекаются?-Прямые АА1 и DC являются скрещивающимися. Сформулируйтеопределение скрещивающихся прямых.-Какую вы можете поставить цель сегодняшнего урока?Учитель еще раз проговаривает тему, конкретизирует цель и задачи урока.Работа с учебником страница 15. - Работаем самостоятельно с учебником. Списать определение скрещивающихся прямых. Нарисовать рис.20. - Приведите примеры скрещивающихся прямых с помощью модели многогранников (параллелепипед, тетраэдр), на примере классной комнаты.- Приведите примеры скрещивающихся прямых из жизни.- Самостоятельно оформите в тетради доказательство признака скрещивающихся прямых. - Докажите сами теорему о скрещивающихся прямых. Оформите ее в тетрадях. - Давайте еще раз повторим 3 возможных случая взаимного расположения двух прямых в пространстве: 1) прямые пересекаются, т.е. имеют только одну общую точку; 2) прямые параллельны, т.е. лежат в одной плоскости и не пересекаются;3) прямые скрещиваются, т.е. не лежат в одной плоскости и не пересекаются. Закрепление. Работа с учебником Решить самостоятельно: I вариант – выполнение № 34(а,б), №35 II вариант – выполнение № 34(в,г), №36 Проверка самостоятельной работы упражнения № 34. Подведение итогов - Давайте вспомним с вами, какую цель мы ставили в начале нашего урока. - Достигнута ли нами цель урока?- Какие знания нам пригодились при выполнении заданий на уроке?Домашняя задание № 35,36; выучить доказательство теоремы.Математика 10 класс Урок №20 Дата ___________Тема: Углы с сонаправленными сторонамиЦели: 1) Ввести формулировку и доказательство теоремы о равенстве углов с сонаправленными сторонами; проверить знания по теме «изображение объектов в пространстве».2)3)Ход урока Организационный момент Актуализация опорных знаний учащихся 1. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые:а) Пересекаться?б) Быть скрещивающимися?3. Могут ли скрещивающиеся прямые и быть параллельными прямой ?4. Даны две скрещивающиеся прямые и. Точки и лежат на прямой, точки и лежат на прямой. Как будут расположены прямые и?5. Прямая скрещивается с прямой, а прямая скрещивается с прямой. Следует ли из этого, что прямые и - скрещиваются?6. Каково должно быть взаимное расположение трех прямых, чтобы можно провести плоскость, содержащую все прямые? И зучение нового материала. Любая прямая, например ОО1 (Рис.), рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными.Лучи О2А2 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости.Теорема. Если стороны двух углов сонаправленны, то такие углы равны.(доказательство на доске и в тетрадях) Работа по теме урока №34, 35, 38, 41, 42, 43 Подведение итогов урока Домашнее задание№ 45, 47, 90Математика 10 класс Урок №21 Дата ___________Тема: Угол между прямымиЦели:1) Ввести понятие угла между прямыми, учить находить углы между скрещивающимися прямыми. Рассмотреть задачи в которых используются эти понятия2) Средствами урока воспитывать у учащихся ответственное отношение к учебному труду, волевые качества личности, умение работать в коллективе.3) способствовать развитию пространственного воображения учащихся, умений обосновывать или опровергать выдвигаемые предположения при решении геометрических задач, создать условия для формирования ключевых компетенций учащихся.Ход урока Организационный момент Актуализация опорных знаний учащихся -         Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?-         Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться?б) быть скрещивающимися?-         Могут ли скрещивающиеся прямые a и b быть параллельными прямой с?-         Даны две скрещивающиеся прямые а и b. Точки А и А1 лежат на прямой а, точки В и В1 лежат на прямой b. Как будут расположены прямые АВ и А1В1?-         Прямая а скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, что прямые а и с - скрещиваются? Изучение нового материала. Расположение прямых в пространстве и угол между ними.1.       Пересекающиеся прямые.2.       Параллельные прямые.3.       Скрещивающиеся прямые.Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла. Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения. Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°.Угол между двумя параллельными прямыми равен 0°.  Проговорить метод параллельного переноса при нахождении угла между скрещивающимися прямыми. Закрепление нового материала Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b. а) 90°;                                   б) 45°; в) 60°;                                   г) 90°; д) 90°;                                   е) 90°.1. Устно. Дан куб ABCDA1B1C1D1 (рис. 4).Найдите угол между прямыми. 1) ВС и СС1 (90°); 2) АС и ВС(45°); 3) D1C1 и ВС(90°). 4) А1В1 и АС(45°). 2. Задача № 44 (на доске и в тетрадях).Дано: OB || CD; OA и CD скрещиваются;a) ∠AOB = 40°; б) ∠AOB = 135°; в) ∠AOB = 90° (рис. 5).Найти: угол между ОА и CD. № 40. Дано: а скрещиваются b;   (рис. 7).Определить:  а) а ⊂ α, так как а скрещиваются b, то b ⊄ α.б)  Подведение итогов. Домашнее задание П. 8; 9 № 40; 42.Математика 10 класс Урок №22 Дата ___________Тема: Контрольная работа по теме: «Взаимное расположение прямых в пространстве»Цели:1) Повторить основные определения и понятия стереометрии, связанные с взаимным расположение прямых в пространстве;2) Развивать у учащихся умения анализировать задачу перед выбором способа ее решения; развивать навыки исследовательской деятельности, синтеза, обобщения;3) Предоставить учащимся возможность осознать значимость себя, почувствовать уверенность в своих силах;Ход урока Организационный момент Контрольная работа Вариант 1 Даны параллельные плоскости α и β. Через точки А и В плоскости проведены параллельные прямые, пересекающие плоскость β в точках А1 и В1. Найдите А1В1, если АВ = 5 см. Верно, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости? Две плоскости параллельны между собой. Из точки М, не лежащей ни в одной из этих плоскостей, ни между плоскостями, проведены две прямые, пересекающие эти плоскости соответственно в точках А1 и A2, В1 и В2. Известно, что МА1 = 4 см, В1В2 = 9 см, A1A2 = МВ1. Найдите МА2 и MB2. Вариант 2 Отрезки АВ и CD параллельных прямых заключены между параллельными плоскостями. Найдите АВ, если CD = 3 см. Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости? Из точки О, лежащей вне двух параллельных плоскостей α и β, проведены три луча, пересекающие плоскости α и β соответственно в точках А, В, С и А1, В1, С1 (ОА < ОА1). Найдите периметр А1В1С1, если ОА = m, АА1 = n, АВ = b, ВС = а. Подведение итогов Домашнее задание: решить задачи, с которыми ученик не справился.Математика 10 класс Урок №23 Дата ___________Тема: Параллельные плоскостиЦели:1) Ввести понятие параллельных плоскостей;2) Доказать признак параллельности двух плоскостей; 3) Сформировать у учащихся навыки применения этого признака при решении задач.Ход урока Организационный момент Актуализация знаний учащихся Анализ контрольной работы. 1. Подвести итоги контрольной работы.2. Анализ ошибок, допущенных в работах.Подготовка учащихся к восприятию нового материал. - Сформулировать Аз. - Сформулировать утверждение 1° п. 6. - Признаки подобия треугольников.- Теорема об отношениях площадей подобных треугольников. - Свойство средней линии треугольника. Изучение нового материала 1. Определение параллельных плоскостей. 2. По аксиоме 3 плоскости пересекаются по прямой. Но возможен еще один случай взаимного расположения двух плоскостей, если они не имеют общей точки.На доске схема В тетрадях учащихся и на доске рисунки и записи. 3 . Признак параллельности плоскостей.Дано', a n р = М, а е а, b е а. ai n bl9 а\ g р, bi е р. а || b || (рис. 3). Доказать: а || р.Доказательство: От противного.Пусть а п р = с, 1) Тогда а || р, а а а, а п р = с, значит, а || с (по утверждению 1° п. 6). 2) b || р, b с: а, а п р = с, значит, b || с. 3) Имеем а || Ь, то есть через точку Ма ||рпроходят две прямые а и Ь, параллельные прямой с. Получили про­ тиворечие. Значит, а || р. Закрепление изученного материала Ле 51. (еще один признак параллельности плоскостей).Дано: т с\ п = X, т е а, п е а, т || р, п || р (рис. 4).Доказать: а || р.Д оказательство: Допустим, что а и р не параллельны. Тогда они пересекаются по некоторой прямой с. Так как т || р, п || р, то по утверждению 1° т || с, п || с. Получаем, что через точку К проходят две прямые, параллельные прямой с, что невозможно по. теореме о параллельных прямых. Получили противоречие. Значит, а || р. №53, Дано\ отрезки А\А2, В Д 2, С[С2лежат в одной плоскости и имеет об- ю середину - точку О (рис. 5). Доказать: АД\С\ ЦА2В2С2.Доказательство:1) А\А2 и В Д 2 лежат в одной плоско­ сти по следствию из А\ (через две пересекающиеся прямые проходит плоскость, и притом только одна). А Д \А 2В2 - параллелограмм (диагонали четырехугольника пересекаются и в точке пересечения делятся пополам). Следовательно, А Д } ЦА2В2. 2) Аналогично Л1Л2 и С]С2 лежат в одной плоскости. А\С\А2С2 па­ раллелограмм. Отсюда, AiCi || А2С2. 3) В\А\ гл A [Cj = Aif В2А2 гл А2С2 = А2.П о признаку параллельности плоскостей АД\С\ || А2В2С2.№ 54. Дано: ЛАОС. В <£ ADC. М, N, Р - середины ВА, ВС, BD соответственно. = 48 см2 (рис. 6).Доказать: a) MPN || ADC.б) Найти: Smnp-Решение:а) В &ABD: М Р -средняя линия, MP || AD.В Д BCD: PN - средняя линия PN || DC.M Pc\PN=P,ADr\DC=D. По призна­ку параллельности двух плоскостей (MNP) || (ADC). Что и требовалось до­ казать. б) /N M P = Z.CAD, /M N P = /AC D как углы с сонаправленными сто- 5 ( MN А2ронами, поэтому AMPN

Тема: Параллельные плоскостиЦели:1) Рассмотреть свойства параллельных плоскостей; 2) Сформировать навык применения изученных свойств параллельных плоскостей при решении задач.3) Средствами урока воспитывать у учащихся ответственное отношение к учебному труду, волевые качества личности, умение работать в коллективе.Ход урока Организационный момент Актуализация опорных знаний учащихся Теоретический опроса) Один ученик готовит у доски доказательство признака параллельно­ сти двух плоскостей. б) Д ругой записывает на доске решение до­ машней задачи № 55. в) Двое учащихся решают по карточкам ин- диивидуального опроса. 1. Плоскости а и р параллельны, прямая т параллельна плоскости р.Дано\ а || р, т с: а (рис. 1).Доказать', что т || р.Решение’.1) Пусть т не параллельна р. т п р = К, К € р.. к^р2) £ е а Получили противоречие условию а || р. Сле- => а п р . дО вательнО 5 т у р цт о и требовалось доказать. т.к. т е а2 . Две стороны треугольника параллельны плоскости а. Докажите, что и третья сторона параллельна плоскости а.Дано’. &АВС, АВ || а, ВС || а. (рис. 2).Доказать’. АС || а.Решение'. Если две пересекающиеся прямые плоскости АВС параллельны плоскости а, то (АВС) || а. Так как AC cz (АВС), а (АВС) || а, то АС || а. Что и требовалось доказать.г) Фронтальный теоретический опрос- сформулируйте определение параллельных плоскостей; - укажите модели параллельных плоскостей на предметах классной обстановки; - сформулируйте признак параллельности плоскостей.Выслушивается доказательство теоремы и решение задачи № 55. Изучение нового материала 1. Рассмотреть свойства параллельных плос­ костей. 1. Дано: а || р, у п а = а, у п р = b (рис. 3).Доказать: а || Ь.Доказательство: Предположим, что а п Ь.Тогда а и р имели бы общую точку, что невоз­ можно, так как а || р по условию. Итак, а и b лежат в одной плоскости у и не пересекаются.Значит, а || Ь. Свойство доказано.2. Дано'. АВ || CD, а || р (рис. 4).Доказать'. АВ = CD.Доказательство:71у п а .у п р а|1Р => по свойству 1° АС || BD.2) В четырехугольнике ABCDAC\\BDAB\\CD=> ABCD- параллелограммВ параллелограмме противоположные сто­ роны равны. Значит, АВ = CD. Что и требова­ лось доказать. Закрепление изученного материала 1 . Решение задачи 58 Дано: а || р, а пересекается с у (рис. 5).Доказать, что р пересекается с у.Решение: Пусть у пересекает а по прямой а.Проведем в плоскости у прямую Ь, пересекаю­ щую а. Прямая b пересекает а, поэтому она пересекает параллельную ей плоскость р (зада­ ча № 55). Следовательно, и плоскость у, в кото­ рой лежит прямая Ь, пересекает плоскость р.2. Задача 636 Дано: а ||р , /ВАС. ar>AB=Alt рг^А В А 2,а п АС=Вь р n АС=В2, А\В\ = 18 см, ААi = 24 см, 3АА2 - — А\А2 (рис. 6).Найти: А2В2, АА2.Решение: 1. (ВАС)су<1=А\В\, (ВАС) п р = А2В2. Таккак а || р, по свойству 1° параллельных плоскостей А \В\ || А2В2. 2. В (ВАС) ДА1АВ4А2АВ2 (по двум углам: /А — общий, = /А А 2В2 как соот- ветственные при параллельных прямых AjBi и А2В2 и секущей АВ). Из подобия треугольников следует, что=АА2=АА1+А,А2 = 24 + А}А2,24+А1А2= 1 а ,А2, — А,А2 = АА, А,В, 2 2A D= 24, А ,А2 = 24 • 2 = 48 (см); АА2 = 48 + 24 = 72 (см); , „ 7218 с л , хА2В2 = 24 = 54 СМ '(Ответ: 54 см = А2В2, АА2 = 72 см.) Самостоятельная работа (см. приложение) Подведение итогов Домашнее заданиеП. 11 № 59, 63а, 64.Математика 10 класс Урок №25 Дата ___________Тема: ТетраэдрЦели:1) Повторит понятие многоугольника в планиметрии2) Ввести понятие тетраэдра; 3) Рассмотреть задачи, связанные с тетраэдром.Ход урока Организационный момент Актуализация опорных знаний учащихся I) Один ученик записывает на доске решение домашней задачи № 63 а.Д ано', а || р, ЛАВС,А} = а n АВ, А2 = р п АВ, Bi = а п АС, В2 Р п АС;AjA2 = 2AiAt AjA2 = 12 см, ABi = 5 см. (рис. 1). Найти: АА2, АВ2.Решение:1. AiBi ЦА2В2 (по свойству 1° параллельных плоскостей).2. ЛА2АВ2 ооЛА7АВу, = АА2 АВ23. Так как А/А2 = 2 AjA и А {А2 = 12 см, то А}А = 1 2 :2 = 6 см. 4. АА2 = 12 + 6 = 18 см. 5.АХА АВХ 6 _ 5АА2 АВ2 18 АВ2АВ2 =15 см.(Ответ: АА2 = 18см, АВ2 = 15 см.) 2) Двое решают по карточкам индивидуального опроса.I. Отрезки АВ, АС и AD не лежат в одной плоскости. Точки К, M a N - соответственно их середины. а) Докажите, что плоскости BCD и KMN параллельны. б) Найдите площадь &ВСД, если = 36 м2.(Ответ: SBcd = 144 м2.)II. Три прямые, проходящие через точку М и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках А }, В и С, а вторую - в точках Л/, В} и Chа) Докажите, что ABC

, шесть ребер и четыре вершины.

Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. На рис. 34 учебника AD и ВС, BD и АС, CD и АВ.

Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие - боковыми гранями.

4) Изображение тетраэдра на плоскости (рис. 5).

  1. Закрепление изученного материала

1) № 68 (устно) по готовому чертежу (рис. 6).

2) № 69. Дано: SABC - тетраэдр, МА = MB, BN = NC,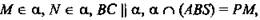 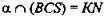  (рис. 7).

Доказать: PM|| KN.

1.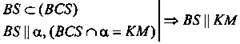   (по свойству 1°).

2.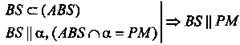   (по свойству 1°).

3. BS || KN, BS || PM, KN || РМ (по теореме о параллельности трех прямых).

3) № 716. Дано: DABC - тетраэдр, M ∈ DB, N ∈ DC, К ∈ ВС (рис. 8).

Построить: точку М1.

Условие: M1 = KN ∩ (FBD).
Решение:

1. NK ⊂ (DBC), DB ⊂ (DBC).

2. NK не может быть параллельна прямой DB. Так как NK || (ADB) (по признаку) - это противоречит условию ⇒ NK ∩ DB.

3. DB ⊂ (ADB), то NK ⊂ (ADB) = М1.

4) № 73. Дано: DABC — тетраэдр, М ∈ АВ, N ∈ BC, Р ∈ CD, K ∈ AD; МА = MB, NB = NC, PC = PD, AC = 10 см, BD = 12 см, AK = KD (рис. 9).

Доказать: К ∈ (MNP).
Найти: PMNPK.

Решение:

1. (MNP) ∩ (ABC) = MN, MN - средняя линия ΔABC ⇒ MN || AC.

2. MN || (ACD) (по признаку параллельности прямой и плоскости), MN проходит через (MNP), (MNP) || (ACD). Значит, линия пересечения (MNP) и (ACD) параллельна MN.

3. Пусть эта линия пересекается с ребром AD в точке К. Так как РК || MN и MN || АС, то РК || АС, а так как Р - середина AD, то РК - средняя линия ΔACD, то есть К - середина AD.

4.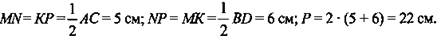   (Ответ: 22 см.)


  1. Подведение итогов

Домашнее задание

П. 12, I уровень: № 67 (a), 70; II уровень: № 67, 71 (a).

Смотрите также файлы