ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 88
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Какая прогрессия называется бесконечно убывающей?
Какова формула суммы такой прогрессии?
№22(1) – у доски
№22(2) – работа в группах
4)Работа со степенями
Какие свойства мы применяем при работе со степенями? – работа в группах (продолжить формулу)
№77(2) – у доски
№78(2) – у доски
№77(1) – в группах
№78(1) – в группах
№84(1,3,) - у доски
№84(2,4) – в группах
Контроль усвоения (по ситуации) (5мин)
III. Подведение итогов
Домашнее задание №94, №95
Математика 10 класс Дата ___________
Тема: Контрольная работа по теме Действительные числа
Цели:
1) уметь выполнять преобразование выражений, используя свойства степени, сравнивать выражения, содержащие степени с рациональным показателем
2) развитие навыка само- и взаимоконтроля; развитие интеллектуальных способностей, мыслительных умений,
3) воспитание познавательного интереса к предмету, воспитание ответственности за выполняемую работу, способствовать созданию атмосферы активного творческого труда.
Ход урока:
1. Организационный момент
Проверка домашнего задания
II. Выполнение письменной контрольной работы


III. Подведение итогов
Домашнее задание №99, №100
Математика 10 класс Дата ___________
Тема: Предмет стереометрия
Цели:
1) ознакомить учащихся с курсом стереометрии, ввести понятие стереометрии, основных фигур стереометрии, рассмотреть аксиомы стереометрии.
2) умение выстраивать аргументацию, приводить примеры и контрпримеры
3) умение организовывать и планировать учебное сотрудничество с учителем и сверстниками, умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем
Ход урока:
I. Организационный момент
II Изучение нового материала
Стереометрия – это раздел геометрии, который изучает свойства фигур в пространстве.
Основные фигуры стереометрии: точка, прямая, плоскость.
Аксиома – это утверждение, которое принимается без доказательства.
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна.
А2. Если две точки прямой лежат в плоскости, то и вся эта прямая лежит в плоскости.
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
III. Закрепление
с. 7 № 1 а, б, № 2 а, № 3 (устно)
№ 1 а) PE ϵ (ADB), MK ϵ (BDC), BD ϵ (ADB), (ABC), AB ϵ (ADB), (ABC), CE ϵ (ABC), (DEC)
№ 1 б) DK ∩ (ABC) в тоске С; CE ∩ (ADB) в точке Е.
№ 2 а) в плоскости (DCC1); D, D1, C, C1, K, M, R.
в плоскости (BQC); B, B1, C, C1, P, M, Q.
№ 3 а) да, аксиома 1
б) неверно,
в) неверно
г) неверно
IV. Подведение итогов
Домашнее задание с. 3-7, решить № 1 в, г, № 2 б
Математика 10 класс Дата ___________
Тема: Основные понятия и аксиомы стереометрии
Цели:
1) повторить аксиомы планиметрии; изучить аксиомы стереометрии; ознакомить учащихся с содержанием курса стереометрии.
2) сформировать у учащихся представление о стереометрии как о разделе геометрии, изучающем свойства фигур в пространстве, сформулировать основные аксиомы стереометрии;
3) Сформировать представления учащихся об аксиомах стереометрии, взаимном расположении прямой и плоскости, плоскостей в пространстве, способах задания плоскости в пространстве.
Ход урока:
I. Организационный момент
II. Изучение нового материала
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
Простейшие фигуры в пространстве: точка, прямая, плоскость.
Плоскость.

Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
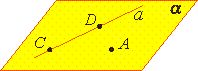
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит
через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко
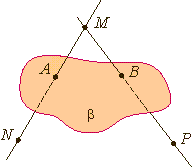
Аксиома 1.
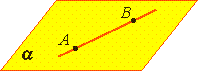
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
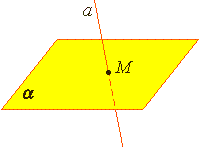
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
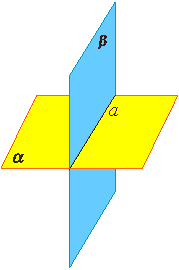
Аксиома 3.
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты
.
Теорема 1.
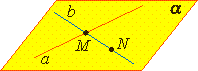
Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.
Теорема 2.
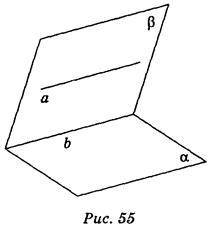
Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
III. Закрепление изученного материала
1. Прочитать формулировки аксиом А1—А3.
2. Решаем задачи:
Учащиеся читают условие задачи по учебнику стр. 7—8 и дают ответ с объяснениями.
Задача 1 (а, б) с. 7.
Ответ:
а) Точки Р и Е лежат в плоскости (АDВ), а значит и прямая РЕ лежит в плоскости (АDВ) (по А2). Аналогично МК лежит в плоскости (ВDС). Точки В и D лежат одновременно в плоскостях (АDВ) и (ВDС), а значит прямая ВD лежит в плоскостях (АDВ) и (АВС).
Аналогично АВ лежит в плоскостях (АDВ) и (АВС).
Точки С и Е лежат одновременно в плоскостях (АВС) и (DЕС), а значит прямая СЕ лежит в этих же плоскостях.
б) Заметим, что точка С лежит на прямой (DК) и в плоскости АВС, а следовательно, DК∩(АВС) в точке С, так как точек пересечения более одной (прямая не лежит в плоскости), то это единственная точка.
Аналогично СЕ пересекается с плоскостью (АDВ) в точке Е.
Задача 2(а) с. 7.
Ответ: а) В плоскости DСС1: D, С, С1, D1, К, M, R (см. №1). В плоскости ВQС: В1, В, Р, Q, С1, М, С.
Повторить аксиомы планиметрии.
Выучить аксиомы А1—А3.
Прочитать пункт 1—2.
Задача 1(в, г)
Ответы:
в) в плоскости АDВ лежат точки: А, D, В, Е, Р, М, так как точка Е лежит на прямой АВ, а значит, и в плоскости АВD. В плоскости DВС лежат точки: D, В, С, M, К
г) плоскости АВС и DСВ пересекаются прямой ВС, так как обе точки В и С лежат в обеих плоскостях. Аналогично: АВD пересекается с СDА по прямой АD. Так как точка Е принадлежит РD, значит, Е принадлежит РDС и так как точка С принадлежит РDС, то прямая СЕ принадлежит РDС, а так как СЕ принадлежит АВС, то плоскости АВС и РDС пересекаются по прямой СЕ.
Задача 2 (б, д)
Ответы:
б) АА1В1; АА1D1.
д) МК∩DС = R; В1С1∩ВР =Q; С1М∩DС = С.
IV. Подведение итогов
Мы познакомились с новым разделом геометрии — стереометрией, узнали новые аксиомы и использовали их при решении задач.
Что нового вы узнали на сегодняшнем уроке?
Домашнее задание
Повторить аксиомы планиметрии.
Выучить аксиомы А1—А3.
Прочитать пункт 1—2.
Математика 10 класс Дата ___________
Тема: Первые следствия из теорем
Цели:
1) повторить аксиомы стереометрии и применение их при решении задач домашнего задания;
2) научить применять следствия из аксиом при решении задач, а также закрепить умение применять аксиомы стереометрии при решении задач;
3) формировать умения работать в группе.
Ход урока:
I. Организационный момент
II. Изучение нового материала
Рассмотрим и докажем следствия из аксиом. Два следствия есть в учебнике , их будут изучать первая и вторая группа. А потом докажут у доски. Третье следствие «Через две параллельные прямые можно провести плоскость и притом только одну» будет доказывать третья группа самостоятельно.
Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.
Учащиеся записывают формулировку в тетради и, отвечая на вопросы учителя, делают соответствующие записи и рисунки в тетрадь.
- Что дано в теореме? (прямая и не лежащая на ней точка)
- Что надо доказать? (проходит плоскость; одна)
- Что можно использовать для доказательства? (аксиомы стереометрии)
- Какая из аксиом позволяет построить плоскость? (А1, через три точки проходит плоскость и притом только одна)
- Что есть в данной теореме и чего не хватает для использования А1 (имеем – точку; необходимы – еще две точки)
- Где построим еще две точки? (на данной прямой)
- Какой вывод можем сделать? ( через три точки строим плоскость)
- Принадлежит ли данной плоскости прямая? ( да)
- На основании чего можно сделать такой вывод? ( на основании А2: если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости)
- Сколько плоскостей можно провести через данные прямую и данную точку? (одну)
- Почему? (так как плоскость, проходящая через прямую и плоскость, проходит через данную точку и две точки на прямой, значит по А1 эта плоскость – единственная)
Теорема 2. Через две пересекающиеся прямые проходит плоскость и притом только одна.
Учащиеся доказывают теорему самостоятельно, затем прослушиваются несколько доказательств и делаются дополнения и уточнения (если они необходимы)
Обратить внимание на то, что доказательство опирается не на аксиомы, а на следствие 1.
Теорема 3. Доказывает представитель от третьей группы учащихся.
III. Закрепление изученного материала
Учащиеся решают задачи № 7, 10, 14 из учебного пособия, делая соответствующие рисунки и записи на доске и в тетрадях.
IV. Подведение итогов:
- Сформулируйте аксиомы стереометрии.
- Сформулируйте следствия из аксиом.
Домашнее задание : п.3, №7
Математика 10 класс Дата ___________
Тема: Параллельные прямые в пространстве
Цели:
1) Формирование знаний учащихся определения параллельных прямых в пространстве, теоремы о единственности прямой, параллельной данной, свойств параллельных прямых;
2) развитие аналитического мышления; формирование умений выделять главное и обобщать
3) развитие познавательного интереса к геометрии в пространстве.
Ход урока:
I. Организационный момент
II. Изучение нового материала
1) Вспомним планиметрию.
-Каким может быть взаимное расположение двух прямых на плоскости? (Совпадают, пересекаются, параллельны)
-Какие прямые в планиметрии называются параллельными?
-Перед вами модель куба
-Что вы можете сказать о прямых АВ и CD? (Они лежат в одной плоскости, они не пересекаются, параллельны)
- Являются ли параллельными прямые В1С и С1С, а AD1 и A1D? (нет, они лежат в одной плоскости, но пересекаются)
-Что вы можете сказать о прямых B1C и A1D?
Проблема.
- Лежат ли они в одной плоскости?
(Они лежат в одной плоскости, они параллельны)
-Сделайте вывод, какие прямые в пространстве называются параллельными?
-Вернёмся к модели куба
-Что вы можете сказать о прямых ВС и АА1? (Они не лежат в одной плоскости, не пересекаются и не параллельны)
Такие прямые называются скрещивающимися.
Запись в тетрадь: «Две прямые называются скрещивающимися, если они не лежат в одной плоскости».
2) Являются ли параллельными следующие прямые? Ответ пояснить (слайды №10-11).
3) Делаем вывод о взаимном расположении прямых в пространстве (слайд №12).
4) Докажем теорему о параллельных прямых (слайды №13-14).
5) Учащиеся самостоятельно формулируют определение параллельных отрезков и лучей (слайд №15).
III. Решение задач
Решение у доски с комментариями.
Задача № 17 (слайд №16).
Дано:
М - середина BD;
N - середина CD;
Q - середина АС;
Р - середина АВ;
AD = 12 см; ВС = 14 см.
Найти: PMNQP - ?
Решение:
1. MN || BC (по составу средней линии) ⇒ MN || PQ; PQ || BC.
2. РМ || AD (по составу средней линии) ⇒ PM || QN; NQ || DA.
Значит, MNQP - параллелограмм (по определению) .
3. PQ = 7; РМ = 6 ⇒ PMNQP = 2(7 + 6) = 26 (см).
Ответ: 26 см.
IV. Подведение итогов урока.
- Всегда ли две непересекающиеся прямые в пространстве параллельны?
- Какие две прямые в пространстве называются параллельными?
- Сколько можно провести в пространстве прямых, проходящих через любую точку пространства, параллельных данной прямой?
Домашнее задание П. 4, теорема, задачи № 16, 18(а)
Математика 10 класс Урок №16 Дата ___________
Тема: Параллельность трех прямых
Цели:
1) Рассмотреть взаимное расположение двух прямых в пространстве, теорему о параллельности трех прямых, ввести понятие параллельных прямых в пространстве, сформировать умения применять полученных знания при решении задач.
2) Развивать память, логическое мышление, внимание, умение грамотно излагать собственные мысли, умение применять полученные знания.
3) Воспитывать аккуратность, старательность, ответственность, дисциплинированность, любовь к предмету
Ход урока
-
Организационный момент
-
Актуализация опорных знаний учащихся
1. Какие прямые на плоскости называются параллельными?
2. Как называются углы, образованные при пересечении параллельных прямых секущей?
-
Изучение нового материала
Определение. Две прямые в пространстве называются параллельными, если они не пересекаются и лежат в одной плоскости.
Используя рисунок, назовите параллельные прямые.
Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Задача 1. Вершина Q параллелограмма MNPQ лежит в плоскости α, а точки M, N, и P не лежат в этой плоскости. Докажите, что прямые NM и NP пересекают плоскость α.
Доказательство. Прямая PQ пересекаетплоскость α в точке Q, так как Q ϵ α, поэтому, согласно лемме о пересечении плоскости параллельными прямыми, прямая NM, параллельная PQ, также пересекает плоскость α. Прямая MQ пересекает плоскость α в точке Q, поэтому параллельная ей прямая NP также пересекает плоскость α, что и требовалось доказать.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.
(рассмотреть доказательство теоремы в учебнике стр. 11)
-
Решение задач
Задача 1. Докажите, что если плоскость проходит через прямую, которая параллельна второй плоскости, и пересекает эту плоскость, то прямая пересечения параллельна данной прямой.
К доске вызывается ученик и доказывает задачу с наименьшей помощью со стороны учителя. После того как задача у доски доказана, учитель показывает, как можно было записать доказательство. Обсуждение.
Задача 2. Докажите, что если две плоскости пересекаются,
параллельные одной и той же прямой, то прямая пересечения этих плоскостей параллельна данной прямой. .
Сначала рисунок к задаче и доказательство обсуждается с классом. Затем учащиеся записывают доказательство. После того, как задача решена, учитель показывает, как можно было записать доказательство.
Решить № 26
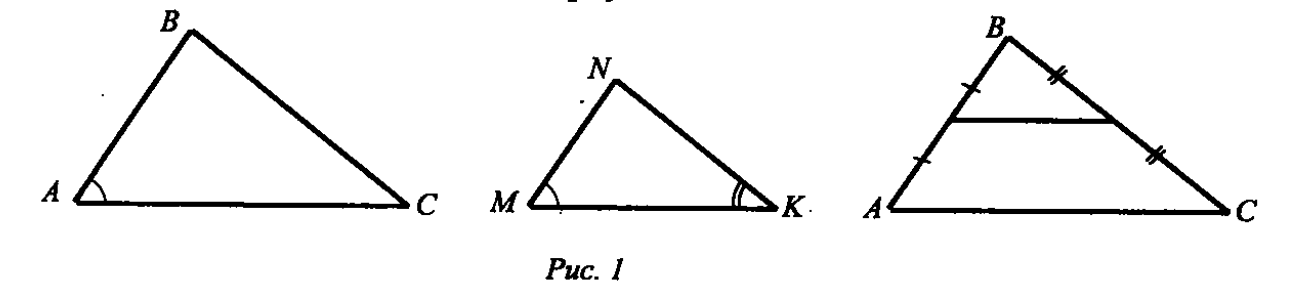
Сторона АС треугольника АВС параллельна плоскости a , а стороны АВ и ВС пересекаются с этой плоскостью в точках М и N. Докажите, что треугольники АВС и МВN подобны. Слайд 11
Перед решением данной задачи необходимо вспомнить признаки подобия треугольников.

Доказательство
1. По утверждению 1° : МN || АC. Тогда угол А = углу ВМN (как односторонние при параллельных прямых).
2. угол В - общий.
З. Таким образом, по двум углам треугольник АВС подобен треугольнику МВN.
К доске вызывается ученик и доказывает задачу с помощью учителя. После того как задача у доски доказана, учитель показывает, как можно было записать доказательство. Обсуждение. Слайд 12.
-
Подведение итогов
1) Сформулируйте признак параллельности прямой и плоскости.
2) Сформулируйте утверждение, обратное признаки параллельности прямой и плоскости. Правильное ли оно?
Домашнее задание
№ 27, № 30, № 31
Математика 10 класс Урок №17 Дата ___________
Тема: Параллельность прямой и плоскости
Цели:
1) Ввести понятия параллельности прямой и плоскости;
2) Воспитывать аккуратность, старательность, ответственность, дисциплинированность, любовь к предмету
3) Сформировать представления учащихся об аксиомах стереометрии, взаимном расположении прямой и плоскости, плоскостей в пространстве, способах задания плоскости в пространстве.
Ход урока
-
Организационный момент
-
Изучение нового материала
Начать с рассмотрения взаимного расположения прямой и плоскости в пространстве
В каком случае прямая и плоскость параллельны (рис. 1. а, б, в)? Прямая и плоскость называются параллельными, если они не имеют общих точек.
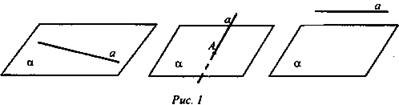
Показать на предметах обстановки классной комнаты прямые, параллельные плоскости пола.
На модели куба (рис. 2) укажите плоскости, параллельные прямой DC, прямой DD1.
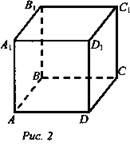
Как установить параллельность прямой и плоскости?
Обратите внимание на модель куба. DC || (AA1B1). В плоскости (AA1B1) имеется прямая АВ || DC; DC || (A1B1C1). В плоскости (А1В1С1) имеется прямая D1C1 || DC. Сделайте предположение. Наличие в плоскости α прямой b || а является признаком, по которому можно сделать вывод о параллельности прямой а и плоскости α.
Теорема:
Дано: а, α; а ∉ α; b ∈ α; а || b (рис. 3).
Доказать, что а || α.
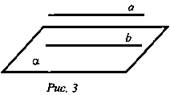 Доказательство: По условию b ∈ α; b || а.
Доказательство: По условию b ∈ α; b || а.
Предположим, что а ∩ α, тогда по лемме о пересечении плоскости параллельными прямыми прямая b ∩ α, но это невозможно, так как b ∈ α. Следовательно, а ∩ α, поэтому а || α и теорема доказана.
Докажем два утверждения, которыми будем пользоваться при решении задач.
1. Если плоскость проходит через данную прямую, параллельную другой плоскости и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Дано: 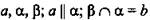 (рис. 4)
(рис. 4)
Доказать: а || b.
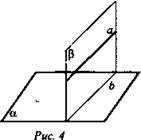
Доказательство: По условию 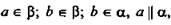 значит, а || b, так как
значит, а || b, так как 
2. Если одна из 2-х параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Дано: а || b; а; а || α (рис. 5).
Доказать: 1) b || α. 2) b ∈ α.
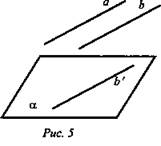 Доказательство: По условию а || b и α || а, следовательно, по лемме о пересечении плоскости параллельными прямыми
Доказательство: По условию а || b и α || а, следовательно, по лемме о пересечении плоскости параллельными прямыми 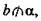 то есть b || α или b ∈ α.
то есть b || α или b ∈ α.
-
Решение задач № 18(б), № 20, 22
-
Подведение итогов
Домашнее задание № 18 (a), 19, 21.
Математика 10 класс Урок №18 Дата ___________
Тема: Параллельность прямой и плоскости
Цели:
-
1) Закрепить и углубить знания и умения применять теоремы о параллельности прямых, прямой и плоскости при решении задач;
-
подготовить учащихся к контрольной работе и зачету по данной теме.
2) Развивать пространственное воображение учащихся при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание;
3) Воспитывать у учащихся ответственное отношение к учебному труду, волю;
Ход урока
-
Организационный момент
-
Устная работа.
1. Верна ли формулировка признака параллельности прямой и плоскости: «Прямая, параллельная какой-либо прямой на плоскости, параллельна и самой плоскости». (Нет, прямая может лежать в плоскости).
2. Прямые а и b параллельны. Какое положение может занимать прямая а относительно плоскости, проходящей через прямую b?
3. Даны прямая и две пересекающихся плоскости. Охарактеризовать все возможные случаи их взаимного расположения.
-
Решение задач по теме урока.
Задача № 22
Дано: A ∈ α, В ∈ α, С ∈ α; AM = МС; BN = NC.
Доказать: MN || α.
Доказательство: MN || АВ (по свойству средней линии), АВ ∈ α; MN || α по признаку.
Перед решением задачи
№ 26 дать понятие отрезка, параллельного плоскости.
«Отрезок параллелен плоскости, если прямая, содержащая этот отрезок, параллельна плоскости».
Задача № 26
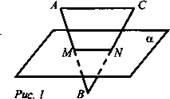
Дано: АС || α, АВ ∩ α = М; СВ ∩ α = N (рис. 1).
Доказать: ΔАВС
ΔMBN.
Доказательство:
1. Докажем, что AC || MN;
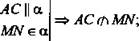
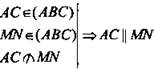 (по определению).
(по определению).
2. Так как АС || MN ⇒ ΔАВС
ΔMBN.
Цели:
1) повторить аксиомы стереометрии и применение их при решении задач домашнего задания;
2) научить применять следствия из аксиом при решении задач, а также закрепить умение применять аксиомы стереометрии при решении задач;
3) формировать умения работать в группе.
Ход урока:
I. Организационный момент
II. Изучение нового материала
Рассмотрим и докажем следствия из аксиом. Два следствия есть в учебнике , их будут изучать первая и вторая группа. А потом докажут у доски. Третье следствие «Через две параллельные прямые можно провести плоскость и притом только одну» будет доказывать третья группа самостоятельно.
Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.
Учащиеся записывают формулировку в тетради и, отвечая на вопросы учителя, делают соответствующие записи и рисунки в тетрадь.
- Что дано в теореме? (прямая и не лежащая на ней точка)
- Что надо доказать? (проходит плоскость; одна)
- Что можно использовать для доказательства? (аксиомы стереометрии)
- Какая из аксиом позволяет построить плоскость? (А1, через три точки проходит плоскость и притом только одна)
- Что есть в данной теореме и чего не хватает для использования А1 (имеем – точку; необходимы – еще две точки)
- Где построим еще две точки? (на данной прямой)
- Какой вывод можем сделать? ( через три точки строим плоскость)
- Принадлежит ли данной плоскости прямая? ( да)
- На основании чего можно сделать такой вывод? ( на основании А2: если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости)
- Сколько плоскостей можно провести через данные прямую и данную точку? (одну)
- Почему? (так как плоскость, проходящая через прямую и плоскость, проходит через данную точку и две точки на прямой, значит по А1 эта плоскость – единственная)
Теорема 2. Через две пересекающиеся прямые проходит плоскость и притом только одна.
Учащиеся доказывают теорему самостоятельно, затем прослушиваются несколько доказательств и делаются дополнения и уточнения (если они необходимы)
Обратить внимание на то, что доказательство опирается не на аксиомы, а на следствие 1.
Теорема 3. Доказывает представитель от третьей группы учащихся.
III. Закрепление изученного материала
Учащиеся решают задачи № 7, 10, 14 из учебного пособия, делая соответствующие рисунки и записи на доске и в тетрадях.
IV. Подведение итогов:
- Сформулируйте аксиомы стереометрии.
- Сформулируйте следствия из аксиом.
Домашнее задание : п.3, №7
Математика 10 класс Дата ___________
Тема: Параллельные прямые в пространстве
Цели:
1) Формирование знаний учащихся определения параллельных прямых в пространстве, теоремы о единственности прямой, параллельной данной, свойств параллельных прямых;
2) развитие аналитического мышления; формирование умений выделять главное и обобщать
3) развитие познавательного интереса к геометрии в пространстве.
Ход урока:
I. Организационный момент
II. Изучение нового материала
1) Вспомним планиметрию.
-Каким может быть взаимное расположение двух прямых на плоскости? (Совпадают, пересекаются, параллельны)
-Какие прямые в планиметрии называются параллельными?
-Перед вами модель куба
-Что вы можете сказать о прямых АВ и CD? (Они лежат в одной плоскости, они не пересекаются, параллельны)
- Являются ли параллельными прямые В1С и С1С, а AD1 и A1D? (нет, они лежат в одной плоскости, но пересекаются)
-Что вы можете сказать о прямых B1C и A1D?
Проблема.
- Лежат ли они в одной плоскости?
(Они лежат в одной плоскости, они параллельны)
-Сделайте вывод, какие прямые в пространстве называются параллельными?
-Вернёмся к модели куба
-Что вы можете сказать о прямых ВС и АА1? (Они не лежат в одной плоскости, не пересекаются и не параллельны)
Такие прямые называются скрещивающимися.
Запись в тетрадь: «Две прямые называются скрещивающимися, если они не лежат в одной плоскости».
2) Являются ли параллельными следующие прямые? Ответ пояснить (слайды №10-11).
3) Делаем вывод о взаимном расположении прямых в пространстве (слайд №12).
4) Докажем теорему о параллельных прямых (слайды №13-14).
5) Учащиеся самостоятельно формулируют определение параллельных отрезков и лучей (слайд №15).
III. Решение задач
Решение у доски с комментариями.
Задача № 17 (слайд №16).
Дано:
М - середина BD;
N - середина CD;
Q - середина АС;
Р - середина АВ;
AD = 12 см; ВС = 14 см.
Найти: PMNQP - ?
Решение:
1. MN || BC (по составу средней линии) ⇒ MN || PQ; PQ || BC.
2. РМ || AD (по составу средней линии) ⇒ PM || QN; NQ || DA.
Значит, MNQP - параллелограмм (по определению) .
3. PQ = 7; РМ = 6 ⇒ PMNQP = 2(7 + 6) = 26 (см).
Ответ: 26 см.
IV. Подведение итогов урока.
- Всегда ли две непересекающиеся прямые в пространстве параллельны?
- Какие две прямые в пространстве называются параллельными?
- Сколько можно провести в пространстве прямых, проходящих через любую точку пространства, параллельных данной прямой?
Домашнее задание П. 4, теорема, задачи № 16, 18(а)
Математика 10 класс Урок №16 Дата ___________
Тема: Параллельность трех прямых
Цели:
1) Рассмотреть взаимное расположение двух прямых в пространстве, теорему о параллельности трех прямых, ввести понятие параллельных прямых в пространстве, сформировать умения применять полученных знания при решении задач.
2) Развивать память, логическое мышление, внимание, умение грамотно излагать собственные мысли, умение применять полученные знания.
3) Воспитывать аккуратность, старательность, ответственность, дисциплинированность, любовь к предмету
Ход урока
-
Организационный момент -
Актуализация опорных знаний учащихся
1. Какие прямые на плоскости называются параллельными?
2. Как называются углы, образованные при пересечении параллельных прямых секущей?
-
Изучение нового материала
Определение. Две прямые в пространстве называются параллельными, если они не пересекаются и лежат в одной плоскости.
Используя рисунок, назовите параллельные прямые.
Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Задача 1. Вершина Q параллелограмма MNPQ лежит в плоскости α, а точки M, N, и P не лежат в этой плоскости. Докажите, что прямые NM и NP пересекают плоскость α.
Доказательство. Прямая PQ пересекаетплоскость α в точке Q, так как Q ϵ α, поэтому, согласно лемме о пересечении плоскости параллельными прямыми, прямая NM, параллельная PQ, также пересекает плоскость α. Прямая MQ пересекает плоскость α в точке Q, поэтому параллельная ей прямая NP также пересекает плоскость α, что и требовалось доказать.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.
(рассмотреть доказательство теоремы в учебнике стр. 11)
-
Решение задач
Задача 1. Докажите, что если плоскость проходит через прямую, которая параллельна второй плоскости, и пересекает эту плоскость, то прямая пересечения параллельна данной прямой.

К доске вызывается ученик и доказывает задачу с наименьшей помощью со стороны учителя. После того как задача у доски доказана, учитель показывает, как можно было записать доказательство. Обсуждение.
Задача 2. Докажите, что если две плоскости пересекаются,
параллельные одной и той же прямой, то прямая пересечения этих плоскостей параллельна данной прямой. .

Сначала рисунок к задаче и доказательство обсуждается с классом. Затем учащиеся записывают доказательство. После того, как задача решена, учитель показывает, как можно было записать доказательство.
Решить № 26
Сторона АС треугольника АВС параллельна плоскости a , а стороны АВ и ВС пересекаются с этой плоскостью в точках М и N. Докажите, что треугольники АВС и МВN подобны. Слайд 11
Перед решением данной задачи необходимо вспомнить признаки подобия треугольников.

Доказательство
1. По утверждению 1° : МN || АC. Тогда угол А = углу ВМN (как односторонние при параллельных прямых).
2. угол В - общий.
З. Таким образом, по двум углам треугольник АВС подобен треугольнику МВN.
К доске вызывается ученик и доказывает задачу с помощью учителя. После того как задача у доски доказана, учитель показывает, как можно было записать доказательство. Обсуждение. Слайд 12.
-
Подведение итогов
1) Сформулируйте признак параллельности прямой и плоскости.
2) Сформулируйте утверждение, обратное признаки параллельности прямой и плоскости. Правильное ли оно?
Домашнее задание
№ 27, № 30, № 31
Математика 10 класс Урок №17 Дата ___________
Тема: Параллельность прямой и плоскости
Цели:
1) Ввести понятия параллельности прямой и плоскости;
2) Воспитывать аккуратность, старательность, ответственность, дисциплинированность, любовь к предмету
3) Сформировать представления учащихся об аксиомах стереометрии, взаимном расположении прямой и плоскости, плоскостей в пространстве, способах задания плоскости в пространстве.
Ход урока
-
Организационный момент -
Изучение нового материала
Начать с рассмотрения взаимного расположения прямой и плоскости в пространстве
В каком случае прямая и плоскость параллельны (рис. 1. а, б, в)? Прямая и плоскость называются параллельными, если они не имеют общих точек.

Показать на предметах обстановки классной комнаты прямые, параллельные плоскости пола.
На модели куба (рис. 2) укажите плоскости, параллельные прямой DC, прямой DD1.

Как установить параллельность прямой и плоскости?
Обратите внимание на модель куба. DC || (AA1B1). В плоскости (AA1B1) имеется прямая АВ || DC; DC || (A1B1C1). В плоскости (А1В1С1) имеется прямая D1C1 || DC. Сделайте предположение. Наличие в плоскости α прямой b || а является признаком, по которому можно сделать вывод о параллельности прямой а и плоскости α.
Теорема:
Дано: а, α; а ∉ α; b ∈ α; а || b (рис. 3).
Доказать, что а || α.
 Доказательство: По условию b ∈ α; b || а.
Доказательство: По условию b ∈ α; b || а.Предположим, что а ∩ α, тогда по лемме о пересечении плоскости параллельными прямыми прямая b ∩ α, но это невозможно, так как b ∈ α. Следовательно, а ∩ α, поэтому а || α и теорема доказана.
Докажем два утверждения, которыми будем пользоваться при решении задач.
1. Если плоскость проходит через данную прямую, параллельную другой плоскости и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Дано:
Доказать: а || b.

Доказательство: По условию
2. Если одна из 2-х параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Дано: а || b; а; а || α (рис. 5).
Доказать: 1) b || α. 2) b ∈ α.
 Доказательство: По условию а || b и α || а, следовательно, по лемме о пересечении плоскости параллельными прямыми
Доказательство: По условию а || b и α || а, следовательно, по лемме о пересечении плоскости параллельными прямыми -
Решение задач № 18(б), № 20, 22 -
Подведение итогов
Домашнее задание № 18 (a), 19, 21.
Математика 10 класс Урок №18 Дата ___________
Тема: Параллельность прямой и плоскости
Цели:
-
1) Закрепить и углубить знания и умения применять теоремы о параллельности прямых, прямой и плоскости при решении задач; -
подготовить учащихся к контрольной работе и зачету по данной теме.
2) Развивать пространственное воображение учащихся при решении геометрических задач, геометрическое мышление, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание;
3) Воспитывать у учащихся ответственное отношение к учебному труду, волю;
Ход урока
-
Организационный момент -
Устная работа.
1. Верна ли формулировка признака параллельности прямой и плоскости: «Прямая, параллельная какой-либо прямой на плоскости, параллельна и самой плоскости». (Нет, прямая может лежать в плоскости).
2. Прямые а и b параллельны. Какое положение может занимать прямая а относительно плоскости, проходящей через прямую b?
3. Даны прямая и две пересекающихся плоскости. Охарактеризовать все возможные случаи их взаимного расположения.
-
Решение задач по теме урока.
Задача № 22
Дано: A ∈ α, В ∈ α, С ∈ α; AM = МС; BN = NC.
Доказать: MN || α.
Доказательство: MN || АВ (по свойству средней линии), АВ ∈ α; MN || α по признаку.
Перед решением задачи
№ 26 дать понятие отрезка, параллельного плоскости.
«Отрезок параллелен плоскости, если прямая, содержащая этот отрезок, параллельна плоскости».
Задача № 26
Дано: АС || α, АВ ∩ α = М; СВ ∩ α = N (рис. 1).
Доказать: ΔАВС
Самостоятельное решение задач по уровням
I уровень
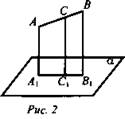
Отрезок АВ не пересекает плоскость α. Через середину отрезка С и концы отрезка А и В проведены прямые, параллельные между собой и пересекающие плоскость α в точках А1, В1, С1.
Вычислить длину отрезка СС1, если АА1 = 5, BB1 = 7.
Дано:
Найти: СС1.
Решение:
1. Докажем, что A1, С1 и В1 лежат на одной прямой. (АА1, ВВ1) = β, β ∩ а = А1В1. Докажем, что С1 ∈ А1В1.
2. Пусть С1 ∈ А1В1, тогда CC1 ∩ β = c, с - прямая пересечения;
3. Так как А1А || ВВ1, значит, А1АВВ1 - трапеция, СС1 - средняя линия
II уровень
Точка М лежит на отрезке АВ. Отрезок АВ пересекается с плоскостью α в точке В. Через А и М проведены параллельные прямые, пересекающие α в точках А1 и M1.
а) Докажите, что А1, М1 и В лежат на одной прямой.
б) Найдите длину отрезка АВ, если АА1 : ММ1 = 3 : 2, AM = 6.
Дано:
Докажите: М1 ∈ А1В.
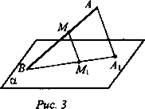
Найдите: АМ = 6.
Решение:
1.
2.
-
Подведение итогов урока.
-Сформулируйте признак параллельности прямой и плоскости.
-Что значит: прямая и плоскость параллельны? - прямая и плоскость параллельны, если они не пересекаются.
-Одна из двух параллельных прямых параллельна некоторой плоскости. Верно ли утверждение, что и вторая прямая параллельна этой плоскости? – да, по 2 свойству параллельности прямой и плоскости.
Домашнее задание: № 24, 28.
Математика 10 класс Урок №19 Дата ___________
Тема: Скрещивающиеся прямые
Цели:
-
1) ввести понятие скрещивающихся прямых;
-
сформулировать и доказать признак скрещивающихся прямых;
-
рассмотреть возможные случаи взаимного расположения прямых в пространстве;
-
2) развивать логическое и пространственное мышление, развивать владение математической речью;
-
умения делать выводы, обобщать и конкретизировать.
-
3) воспитывать умение работать в коллективе;
-
воспитывать познавательную активность, самостоятельность, стремление расширять свой кругозор;
Ход урока
-
Организационный момент
-
Актуализация опорных знаний учащихся
1. Две прямые в пространстве называются параллельными, если они не пересекаются.
2. Прямая а пересекает плоскость α и а║b.Тогда прямая b не пересекает плоскость α.
3. Прямая и плоскость называются параллельными, если они не имеют общих точек.
4. Прямая а║b, а b ║с. Тогда а ∩с.
-
Изучение нового материала.
Б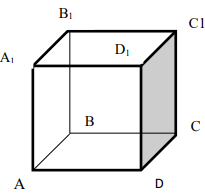 еседа учителя и учащихся по
еседа учителя и учащихся по
параллелепипеду, по взаимному
расположению прямых.
-Являются ли параллельными прямые АА1
и DD1; AA1 и CC1? Почему?
-Являются ли АА1 и DC параллельными?
Они пересекаются?
-Прямые АА1 и DC являются скрещивающимися. Сформулируйте
определение скрещивающихся прямых.
-Какую вы можете поставить цель сегодняшнего урока?
Учитель еще раз проговаривает тему, конкретизирует цель и задачи урока.
Работа с учебником страница 15.
- Работаем самостоятельно с учебником. Списать определение скрещивающихся прямых. Нарисовать рис.20.
- Приведите примеры скрещивающихся прямых с помощью модели многогранников (параллелепипед, тетраэдр), на примере классной комнаты.
- Приведите примеры скрещивающихся прямых из жизни.
- Самостоятельно оформите в тетради доказательство признака скрещивающихся прямых.
- Докажите сами теорему о скрещивающихся прямых. Оформите ее в тетрадях.
- Давайте еще раз повторим 3 возможных случая взаимного расположения двух прямых в пространстве:
1) прямые пересекаются, т.е. имеют только одну общую точку;
2) прямые параллельны, т.е. лежат в одной плоскости и не пересекаются;
3) прямые скрещиваются, т.е. не лежат в одной плоскости и не пересекаются.
-
Закрепление. Работа с учебником
Решить самостоятельно:
I вариант – выполнение № 34(а,б), №35
II вариант – выполнение № 34(в,г), №36
Проверка самостоятельной работы упражнения № 34.
-
Подведение итогов
- Давайте вспомним с вами, какую цель мы ставили в начале нашего урока. - Достигнута ли нами цель урока?
- Какие знания нам пригодились при выполнении заданий на уроке?
Домашняя задание № 35,36; выучить доказательство теоремы.
Математика 10 класс Урок №20 Дата ___________
Тема: Углы с сонаправленными сторонами
Цели:
1) Ввести формулировку и доказательство теоремы о равенстве углов с сонаправленными сторонами; проверить знания по теме «изображение объектов в пространстве».
2)
3)
Ход урока
-
Организационный момент
-
Актуализация опорных знаний учащихся
1. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?
2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые:
а) Пересекаться?
б) Быть скрещивающимися?
3. Могут ли скрещивающиеся прямые и быть параллельными прямой ?
4. Даны две скрещивающиеся прямые и. Точки и лежат на прямой, точки и лежат на прямой. Как будут расположены прямые и?
5. Прямая скрещивается с прямой, а прямая скрещивается с прямой. Следует ли из этого, что прямые и - скрещиваются?
6. Каково должно быть взаимное расположение трех прямых, чтобы можно провести плоскость, содержащую все прямые?
-
И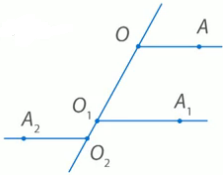 зучение нового материала.
зучение нового материала.
Любая прямая, например ОО1 (Рис.), рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными.
Лучи О2А2 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости.
Теорема. Если стороны двух углов сонаправленны, то такие углы равны.
(доказательство на доске и в тетрадях)
-
Работа по теме урока
№34, 35, 38, 41, 42, 43
-
Подведение итогов урока
Домашнее задание
№ 45, 47, 90
Математика 10 класс Урок №21 Дата ___________
Тема: Угол между прямыми
Цели:
1) Ввести понятие угла между прямыми, учить находить углы между скрещивающимися прямыми. Рассмотреть задачи в которых используются эти понятия
2) Средствами урока воспитывать у учащихся ответственное отношение к учебному труду, волевые качества личности, умение работать в коллективе.
3) способствовать развитию пространственного воображения учащихся, умений обосновывать или опровергать выдвигаемые предположения при решении геометрических задач, создать условия для формирования ключевых компетенций учащихся.
Ход урока
-
Организационный момент
-
Актуализация опорных знаний учащихся
- Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?
- Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться?
б) быть скрещивающимися?
- Могут ли скрещивающиеся прямые a и b быть параллельными прямой с?
- Даны две скрещивающиеся прямые а и b. Точки А и А1 лежат на прямой а, точки В и В1 лежат на прямой b. Как будут расположены прямые АВ и А1В1?
- Прямая а скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, что прямые а и с - скрещиваются?
-
Изучение нового материала.
Расположение прямых в пространстве и угол между ними.
1. Пересекающиеся прямые.
2. Параллельные прямые.
3. Скрещивающиеся прямые.
Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла.
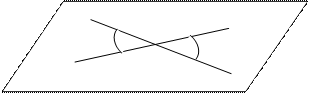
Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.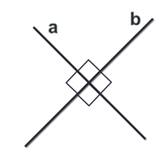
Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°.
Угол между двумя параллельными прямыми равен 0°.
Проговорить метод параллельного переноса при нахождении угла между скрещивающимися прямыми.
-
Закрепление нового материала
Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b.
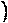
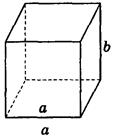 а) 90°;
а) 90°; 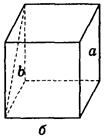 б) 45°;
б) 45°;
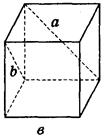 в) 60°;
в) 60°; 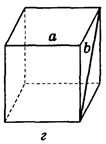 г) 90°;
г) 90°;
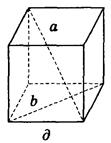 д) 90°;
д) 90°; 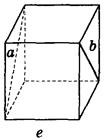 е) 90°.
е) 90°.
1. Устно. Дан куб ABCDA1B1C1D1 (рис. 4).
Найдите угол между прямыми. 1) ВС и СС1 (90°); 2) АС и ВС(45°); 3) D1C1 и ВС(90°). 4) А1В1 и АС(45°).
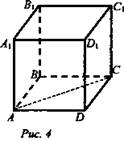
2. Задача № 44 (на доске и в тетрадях).
Дано: OB || CD; OA и CD скрещиваются;
a) ∠AOB = 40°; б) ∠AOB = 135°; в) ∠AOB = 90° (рис. 5).
Найти: угол между ОА и CD.
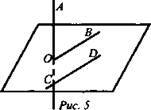
№ 40. Дано: а скрещиваются b; 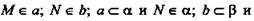
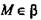 (рис. 7).
(рис. 7).
Определить: 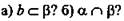
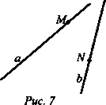
а) а ⊂ α, так как а скрещиваются b, то b ⊄ α.
б) 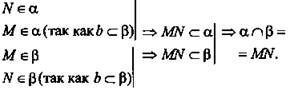
-
Подведение итогов.
Домашнее задание П. 8; 9 № 40; 42.
Математика 10 класс Урок №22 Дата ___________
Тема: Контрольная работа по теме: «Взаимное расположение прямых в пространстве»
Цели:
1) Повторить основные определения и понятия стереометрии, связанные с взаимным расположение прямых в пространстве;
2) Развивать у учащихся умения анализировать задачу перед выбором способа ее решения; развивать навыки исследовательской деятельности, синтеза, обобщения;
3) Предоставить учащимся возможность осознать значимость себя, почувствовать уверенность в своих силах;
Ход урока
-
Организационный момент
-
Контрольная работа
Вариант 1
-
Даны параллельные плоскости α и β. Через точки А и В плоскости проведены параллельные прямые, пересекающие плоскость β в точках А1 и В1. Найдите А1В1, если АВ = 5 см.
-
Верно, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?
-
Две плоскости параллельны между собой. Из точки М, не лежащей ни в одной из этих плоскостей, ни между плоскостями, проведены две прямые, пересекающие эти плоскости соответственно в точках А1 и A2, В1 и В2. Известно, что МА1 = 4 см, В1В2 = 9 см, A1A2 = МВ1. Найдите МА2 и MB2.
Вариант 2
-
Отрезки АВ и CD параллельных прямых заключены между параллельными плоскостями. Найдите АВ, если CD = 3 см.
-
Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?
-
Из точки О, лежащей вне двух параллельных плоскостей α и β, проведены три луча, пересекающие плоскости α и β соответственно в точках А, В, С и А1, В1, С1 (ОА < ОА1). Найдите периметр А1В1С1, если ОА = m, АА1 = n, АВ = b, ВС = а.
-
Подведение итогов
Домашнее задание: решить задачи, с которыми ученик не справился.
Математика 10 класс Урок №23 Дата ___________
Тема: Параллельные плоскости
Цели:
1) Ввести понятие параллельных плоскостей;
2) Доказать признак параллельности двух плоскостей;
3) Сформировать у учащихся навыки применения этого признака при решении задач.
Ход урока
-
Организационный момент
-
Актуализация знаний учащихся
Анализ контрольной работы.
1. Подвести итоги контрольной работы.
2. Анализ ошибок, допущенных в работах.
Подготовка учащихся к восприятию нового материал.
- Сформулировать Аз.
- Сформулировать утверждение 1° п. 6.
- Признаки подобия треугольников.
- Теорема об отношениях площадей подобных треугольников.
- Свойство средней линии треугольника.
-
Изучение нового материала
1. Определение параллельных плоскостей. 2. По аксиоме 3 плоскости пересекаются по прямой. Но возможен еще один случай взаимного расположения двух плоскостей, если они не имеют общей точки.
На доске схема
В тетрадях учащихся и на доске рисунки и записи.

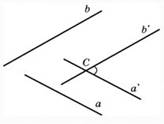
3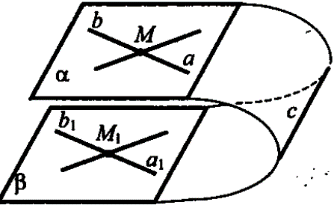 . Признак параллельности плоскостей.
. Признак параллельности плоскостей.
Дано', a n р = М, а е а, b е а. ai n bl9 а\ g р, bi е р. а || b || (рис. 3).
Доказать: а || р.
Доказательство: От противного.
Пусть а п р = с, 1) Тогда а || р, а а а, а п р = с, значит, а || с (по утверждению 1° п. 6). 2) b || р, b с: а, а п р = с, значит, b || с. 3) Имеем а || Ь, то есть через точку М
а ||р
проходят две прямые а и Ь, параллельные прямой с. Получили про тиворечие. Значит, а || р.
-
Закрепление изученного материала
Ле 51. (еще один признак параллельности плоскостей).
Дано: т с\ п = X, т е а, п е а, т || р, п || р (рис. 4).
Доказать: а || р.
Д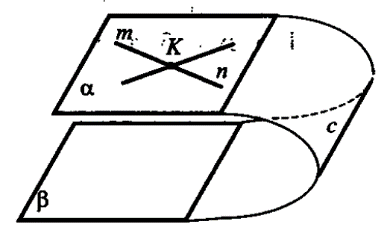 оказательство: Допустим, что а и р не параллельны. Тогда они пересекаются по некоторой прямой с. Так как т || р, п || р, то по утверждению 1° т || с, п || с. Получаем, что через точку К проходят две прямые, параллельные прямой с, что невозможно по. теореме о параллельных прямых. Получили противоречие. Значит, а || р.
оказательство: Допустим, что а и р не параллельны. Тогда они пересекаются по некоторой прямой с. Так как т || р, п || р, то по утверждению 1° т || с, п || с. Получаем, что через точку К проходят две прямые, параллельные прямой с, что невозможно по. теореме о параллельных прямых. Получили противоречие. Значит, а || р.
№53, Дано\ отрезки А\А2, В Д 2, С[С2
лежат в одной плоскости и имеет об- ю середину - точку О (рис. 5). 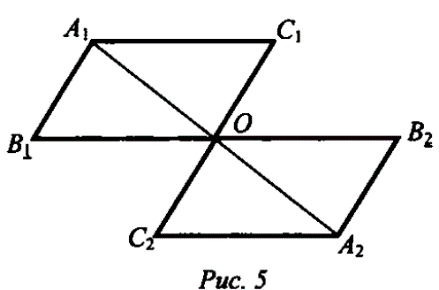
Доказать: АД\С\ ЦА2В2С2.
Доказательство:
1) А\А2 и В Д 2 лежат в одной плоско сти по следствию из А\ (через две пересекающиеся прямые проходит плоскость, и притом только одна). А Д \А 2В2 - параллелограмм (диагонали четырехугольника пересекаются и в точке пересечения делятся пополам). Следовательно, А Д } ЦА2В2. 2) Аналогично Л1Л2 и С]С2 лежат в одной плоскости. А\С\А2С2
па раллелограмм. Отсюда, AiCi || А2С2. 3) В\А\ гл A [Cj = Aif В2А2 гл А2С2 = А2.
П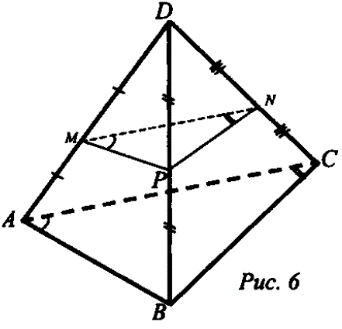 о признаку параллельности плоскостей АД\С\ || А2В2С2.
о признаку параллельности плоскостей АД\С\ || А2В2С2.
№ 54. Дано: ЛАОС. В <£ ADC. М, N, Р -
середины ВА, ВС, BD соответственно. = 48 см2 (рис. 6).
Доказать: a) MPN || ADC.
б) Найти: Smnp-
Решение:
а) В &ABD: М Р -средняя линия, MP || AD.
В Д BCD: PN - средняя линия PN || DC.
M Pc\PN=P,ADr\DC=D. По призна
ку параллельности двух плоскостей (MNP) || (ADC). Что и требовалось до казать. б) /N M P = Z.CAD, /M N P = /AC D как углы с сонаправленными сто- 5 ( MN А2
ронами, поэтому AMPN
AADC по двум углам. = ----- (по
Цели:
-
1) ввести понятие скрещивающихся прямых; -
сформулировать и доказать признак скрещивающихся прямых;
-
рассмотреть возможные случаи взаимного расположения прямых в пространстве;
-
2) развивать логическое и пространственное мышление, развивать владение математической речью; -
умения делать выводы, обобщать и конкретизировать.
-
3) воспитывать умение работать в коллективе; -
воспитывать познавательную активность, самостоятельность, стремление расширять свой кругозор;
Ход урока
-
Организационный момент -
Актуализация опорных знаний учащихся
1. Две прямые в пространстве называются параллельными, если они не пересекаются.
2. Прямая а пересекает плоскость α и а║b.Тогда прямая b не пересекает плоскость α.
3. Прямая и плоскость называются параллельными, если они не имеют общих точек.
4. Прямая а║b, а b ║с. Тогда а ∩с.
-
Изучение нового материала.
Б
 еседа учителя и учащихся по
еседа учителя и учащихся попараллелепипеду, по взаимному
расположению прямых.
-Являются ли параллельными прямые АА1
и DD1; AA1 и CC1? Почему?
-Являются ли АА1 и DC параллельными?
Они пересекаются?
-Прямые АА1 и DC являются скрещивающимися. Сформулируйте
определение скрещивающихся прямых.
-Какую вы можете поставить цель сегодняшнего урока?
Учитель еще раз проговаривает тему, конкретизирует цель и задачи урока.
Работа с учебником страница 15.
- Работаем самостоятельно с учебником. Списать определение скрещивающихся прямых. Нарисовать рис.20.
- Приведите примеры скрещивающихся прямых с помощью модели многогранников (параллелепипед, тетраэдр), на примере классной комнаты.
- Приведите примеры скрещивающихся прямых из жизни.
- Самостоятельно оформите в тетради доказательство признака скрещивающихся прямых.
- Докажите сами теорему о скрещивающихся прямых. Оформите ее в тетрадях.
- Давайте еще раз повторим 3 возможных случая взаимного расположения двух прямых в пространстве:
1) прямые пересекаются, т.е. имеют только одну общую точку;
2) прямые параллельны, т.е. лежат в одной плоскости и не пересекаются;
3) прямые скрещиваются, т.е. не лежат в одной плоскости и не пересекаются.
-
Закрепление. Работа с учебником
Решить самостоятельно:
I вариант – выполнение № 34(а,б), №35
II вариант – выполнение № 34(в,г), №36
Проверка самостоятельной работы упражнения № 34.
-
Подведение итогов
- Давайте вспомним с вами, какую цель мы ставили в начале нашего урока. - Достигнута ли нами цель урока?
- Какие знания нам пригодились при выполнении заданий на уроке?
Домашняя задание № 35,36; выучить доказательство теоремы.
Математика 10 класс Урок №20 Дата ___________
Тема: Углы с сонаправленными сторонами
Цели:
1) Ввести формулировку и доказательство теоремы о равенстве углов с сонаправленными сторонами; проверить знания по теме «изображение объектов в пространстве».
2)
3)
Ход урока
-
Организационный момент -
Актуализация опорных знаний учащихся
1. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?
2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые:
а) Пересекаться?
б) Быть скрещивающимися?
3. Могут ли скрещивающиеся прямые и быть параллельными прямой ?
4. Даны две скрещивающиеся прямые и. Точки и лежат на прямой, точки и лежат на прямой. Как будут расположены прямые и?
5. Прямая скрещивается с прямой, а прямая скрещивается с прямой. Следует ли из этого, что прямые и - скрещиваются?
6. Каково должно быть взаимное расположение трех прямых, чтобы можно провести плоскость, содержащую все прямые?
-
И зучение нового материала.
зучение нового материала.
Любая прямая, например ОО1 (Рис.), рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными.
Лучи О2А2 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости.
Теорема. Если стороны двух углов сонаправленны, то такие углы равны.
(доказательство на доске и в тетрадях)
-
Работа по теме урока
№34, 35, 38, 41, 42, 43
-
Подведение итогов урока
Домашнее задание
№ 45, 47, 90
Математика 10 класс Урок №21 Дата ___________
Тема: Угол между прямыми
Цели:
1) Ввести понятие угла между прямыми, учить находить углы между скрещивающимися прямыми. Рассмотреть задачи в которых используются эти понятия
2) Средствами урока воспитывать у учащихся ответственное отношение к учебному труду, волевые качества личности, умение работать в коллективе.
3) способствовать развитию пространственного воображения учащихся, умений обосновывать или опровергать выдвигаемые предположения при решении геометрических задач, создать условия для формирования ключевых компетенций учащихся.
Ход урока
-
Организационный момент -
Актуализация опорных знаний учащихся
- Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны?
- Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться?
б) быть скрещивающимися?
- Могут ли скрещивающиеся прямые a и b быть параллельными прямой с?
- Даны две скрещивающиеся прямые а и b. Точки А и А1 лежат на прямой а, точки В и В1 лежат на прямой b. Как будут расположены прямые АВ и А1В1?
- Прямая а скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, что прямые а и с - скрещиваются?
-
Изучение нового материала.
Расположение прямых в пространстве и угол между ними.
1. Пересекающиеся прямые.
2. Параллельные прямые.
3. Скрещивающиеся прямые.
Любые две пересекающие прямые лежат в одной плоскости и образуют четыре неразвернутых угла.

Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения.

Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен 90°.
Угол между двумя параллельными прямыми равен 0°.


Проговорить метод параллельного переноса при нахождении угла между скрещивающимися прямыми.
-
Закрепление нового материала
Дано изображение куба. Найдите угол между скрещивающимися прямыми а и b.
 а) 90°;
а) 90°;  б) 45°;
б) 45°; в) 60°;
в) 60°;  г) 90°;
г) 90°; д) 90°;
д) 90°;  е) 90°.
е) 90°.1. Устно. Дан куб ABCDA1B1C1D1 (рис. 4).
Найдите угол между прямыми. 1) ВС и СС1 (90°); 2) АС и ВС(45°); 3) D1C1 и ВС(90°). 4) А1В1 и АС(45°).

2. Задача № 44 (на доске и в тетрадях).
Дано: OB || CD; OA и CD скрещиваются;
a) ∠AOB = 40°; б) ∠AOB = 135°; в) ∠AOB = 90° (рис. 5).
Найти: угол между ОА и CD.

№ 40. Дано: а скрещиваются b;
Определить:

а) а ⊂ α, так как а скрещиваются b, то b ⊄ α.
б)
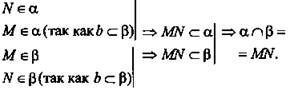
-
Подведение итогов.
Домашнее задание П. 8; 9 № 40; 42.
Математика 10 класс Урок №22 Дата ___________
Тема: Контрольная работа по теме: «Взаимное расположение прямых в пространстве»
Цели:
1) Повторить основные определения и понятия стереометрии, связанные с взаимным расположение прямых в пространстве;
2) Развивать у учащихся умения анализировать задачу перед выбором способа ее решения; развивать навыки исследовательской деятельности, синтеза, обобщения;
3) Предоставить учащимся возможность осознать значимость себя, почувствовать уверенность в своих силах;
Ход урока
-
Организационный момент -
Контрольная работа
Вариант 1
-
Даны параллельные плоскости α и β. Через точки А и В плоскости проведены параллельные прямые, пересекающие плоскость β в точках А1 и В1. Найдите А1В1, если АВ = 5 см. -
Верно, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости? -
Две плоскости параллельны между собой. Из точки М, не лежащей ни в одной из этих плоскостей, ни между плоскостями, проведены две прямые, пересекающие эти плоскости соответственно в точках А1 и A2, В1 и В2. Известно, что МА1 = 4 см, В1В2 = 9 см, A1A2 = МВ1. Найдите МА2 и MB2.
Вариант 2
-
Отрезки АВ и CD параллельных прямых заключены между параллельными плоскостями. Найдите АВ, если CD = 3 см. -
Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости? -
Из точки О, лежащей вне двух параллельных плоскостей α и β, проведены три луча, пересекающие плоскости α и β соответственно в точках А, В, С и А1, В1, С1 (ОА < ОА1). Найдите периметр А1В1С1, если ОА = m, АА1 = n, АВ = b, ВС = а.
-
Подведение итогов
Домашнее задание: решить задачи, с которыми ученик не справился.
Математика 10 класс Урок №23 Дата ___________
Тема: Параллельные плоскости
Цели:
1) Ввести понятие параллельных плоскостей;
2) Доказать признак параллельности двух плоскостей;
3) Сформировать у учащихся навыки применения этого признака при решении задач.
Ход урока
-
Организационный момент -
Актуализация знаний учащихся
Анализ контрольной работы.
1. Подвести итоги контрольной работы.
2. Анализ ошибок, допущенных в работах.
Подготовка учащихся к восприятию нового материал.
- Сформулировать Аз.
- Сформулировать утверждение 1° п. 6.
- Признаки подобия треугольников.
- Теорема об отношениях площадей подобных треугольников.
- Свойство средней линии треугольника.

-
Изучение нового материала
1. Определение параллельных плоскостей. 2. По аксиоме 3 плоскости пересекаются по прямой. Но возможен еще один случай взаимного расположения двух плоскостей, если они не имеют общей точки.
На доске схема
В тетрадях учащихся и на доске рисунки и записи.

3
 . Признак параллельности плоскостей.
. Признак параллельности плоскостей.Дано', a n р = М, а е а, b е а. ai n bl9 а\ g р, bi е р. а || b || (рис. 3).
Доказать: а || р.
Доказательство: От противного.
Пусть а п р = с, 1) Тогда а || р, а а а, а п р = с, значит, а || с (по утверждению 1° п. 6). 2) b || р, b с: а, а п р = с, значит, b || с. 3) Имеем а || Ь, то есть через точку М
а ||р
проходят две прямые а и Ь, параллельные прямой с. Получили про тиворечие. Значит, а || р.
-
Закрепление изученного материала
Ле 51. (еще один признак параллельности плоскостей).
Дано: т с\ п = X, т е а, п е а, т || р, п || р (рис. 4).
Доказать: а || р.
Д
 оказательство: Допустим, что а и р не параллельны. Тогда они пересекаются по некоторой прямой с. Так как т || р, п || р, то по утверждению 1° т || с, п || с. Получаем, что через точку К проходят две прямые, параллельные прямой с, что невозможно по. теореме о параллельных прямых. Получили противоречие. Значит, а || р.
оказательство: Допустим, что а и р не параллельны. Тогда они пересекаются по некоторой прямой с. Так как т || р, п || р, то по утверждению 1° т || с, п || с. Получаем, что через точку К проходят две прямые, параллельные прямой с, что невозможно по. теореме о параллельных прямых. Получили противоречие. Значит, а || р. №53, Дано\ отрезки А\А2, В Д 2, С[С2
лежат в одной плоскости и имеет об- ю середину - точку О (рис. 5).

Доказать: АД\С\ ЦА2В2С2.
Доказательство:
1) А\А2 и В Д 2 лежат в одной плоско сти по следствию из А\ (через две пересекающиеся прямые проходит плоскость, и притом только одна). А Д \А 2В2 - параллелограмм (диагонали четырехугольника пересекаются и в точке пересечения делятся пополам). Следовательно, А Д } ЦА2В2. 2) Аналогично Л1Л2 и С]С2 лежат в одной плоскости. А\С\А2С2