ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 93
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
; 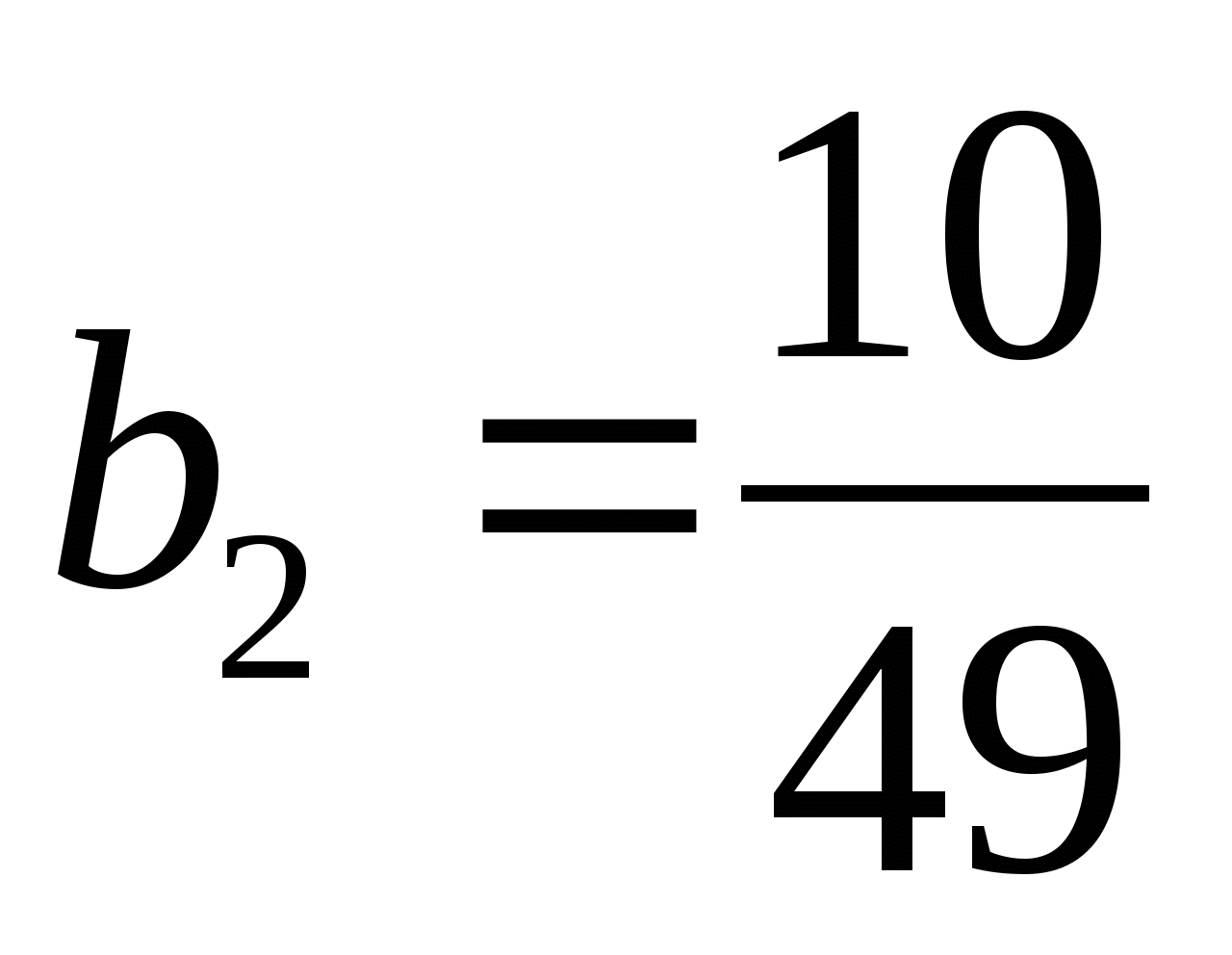 ;
; 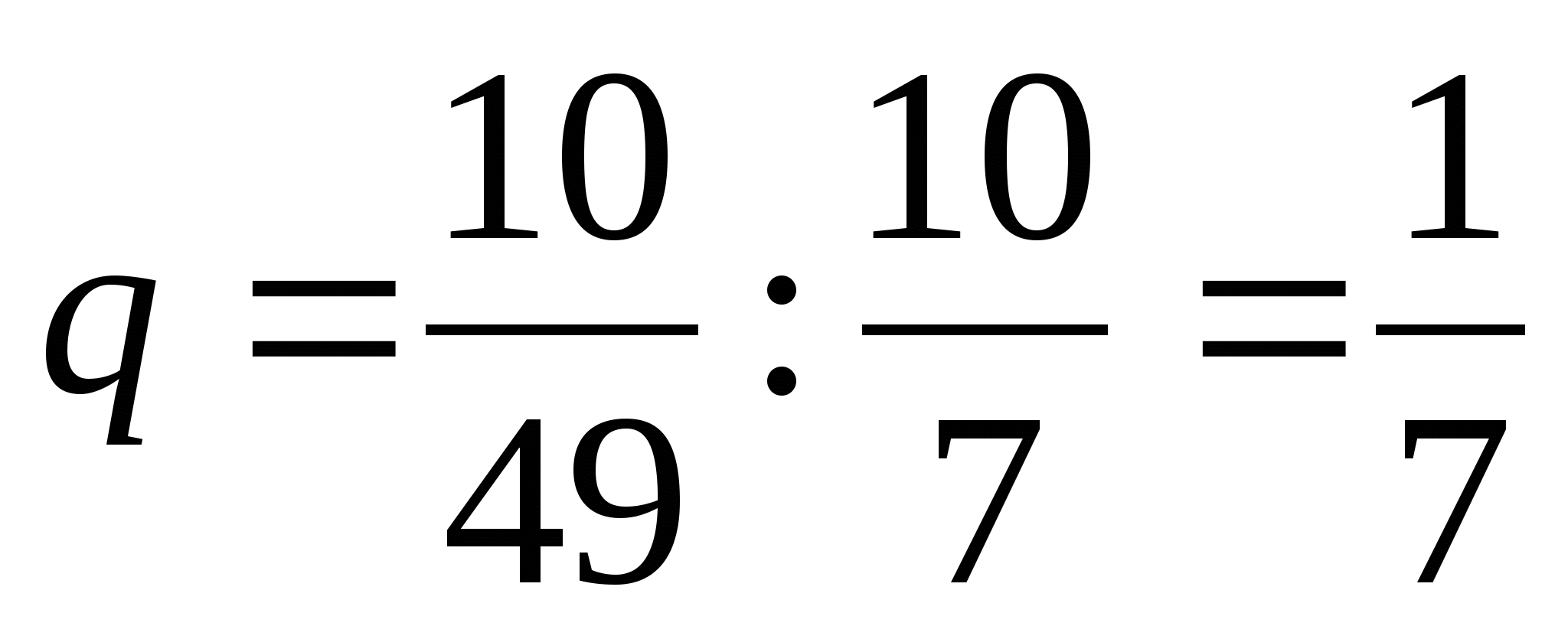 ;
; 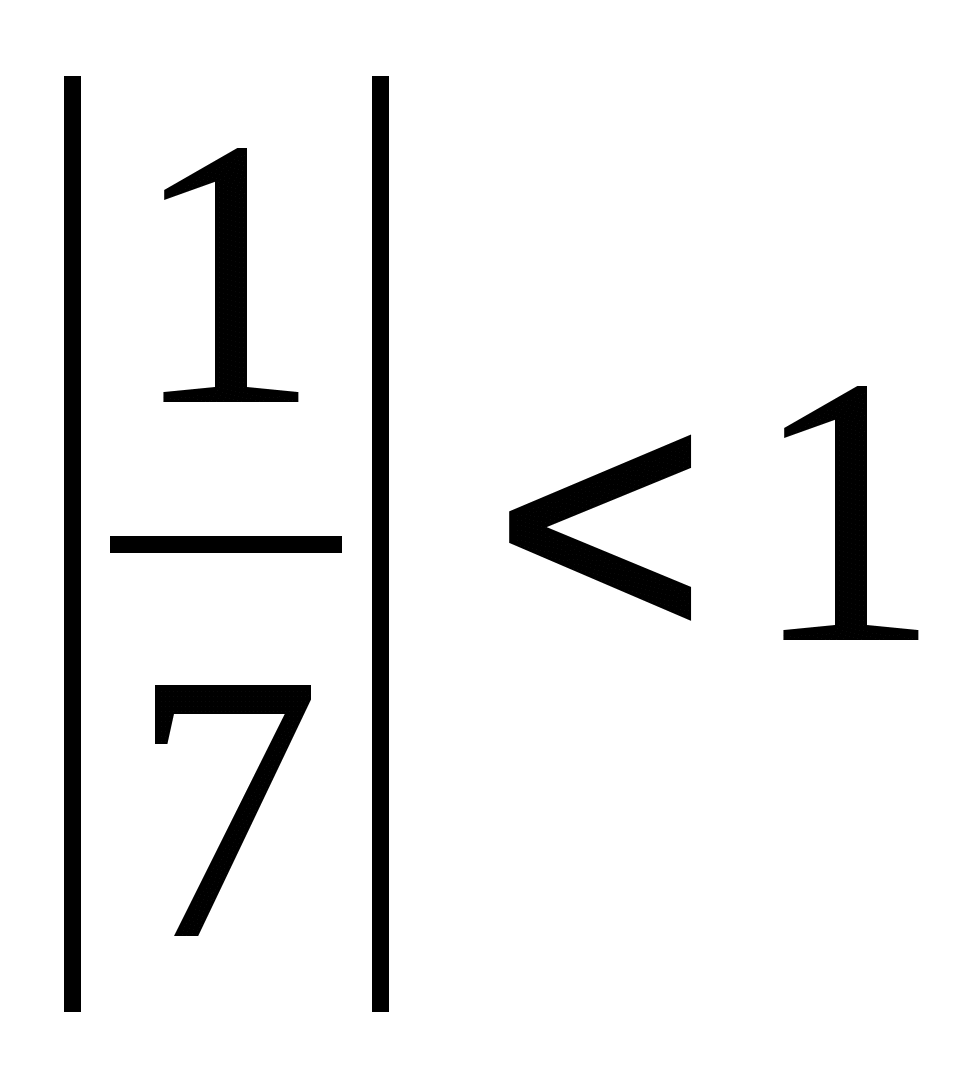 .
.
данная геометрическая прогрессия является бесконечно убывающей.
б) данная последовательность не является бесконечно убывающей геометрической прогрессией.
Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию: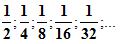
Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.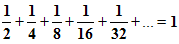
Но в левой части этого равенства – сумма бесконечного числа слагаемых.
Рассмотрим сумму n первых слагаемых.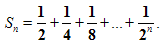
По формуле суммы n первых членов геометрической прогрессии, она равна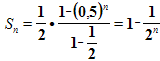 .
.
Если n неограниченно возрастает, то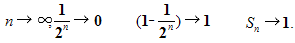
или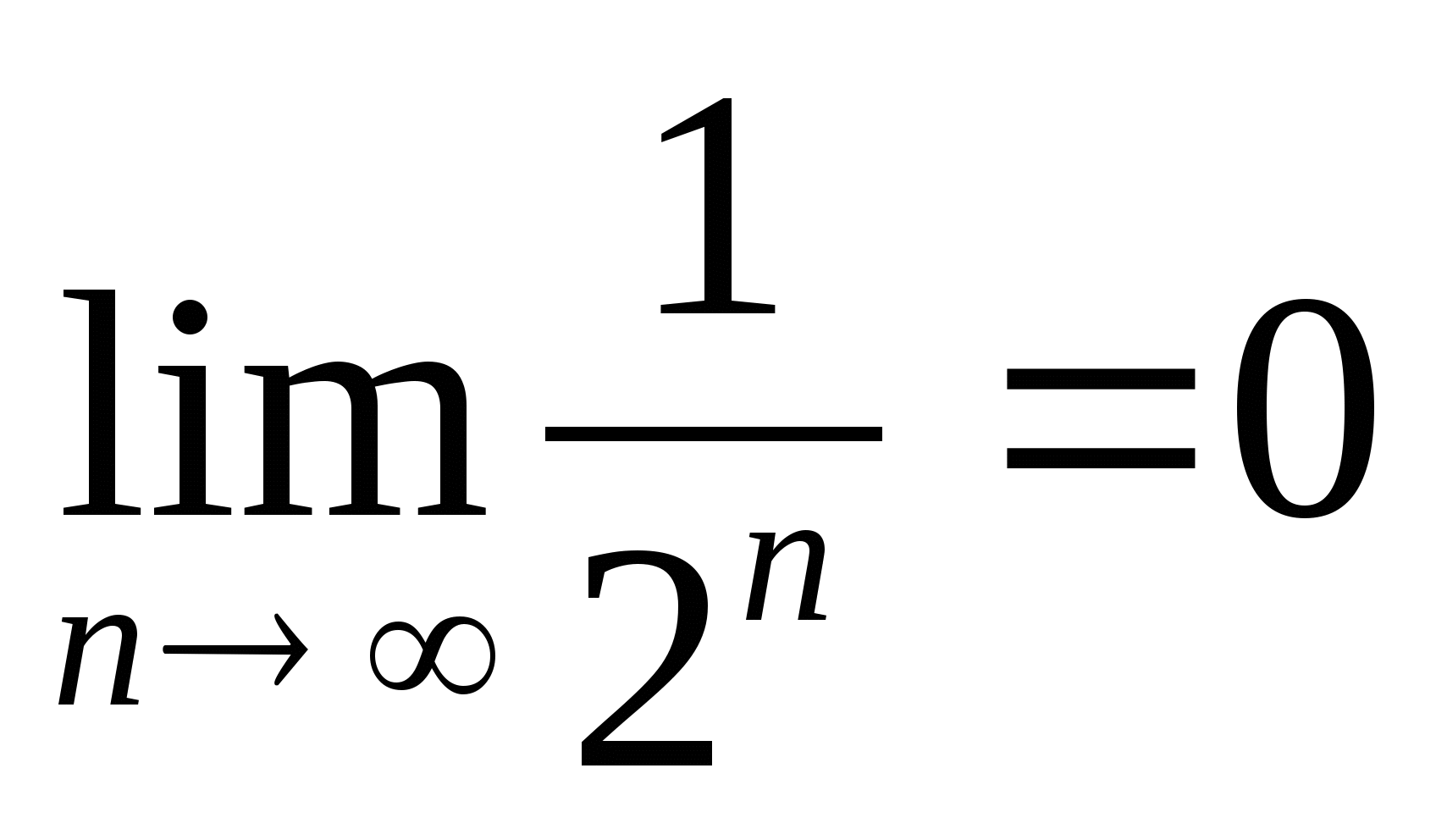 . Поэтому
. Поэтому 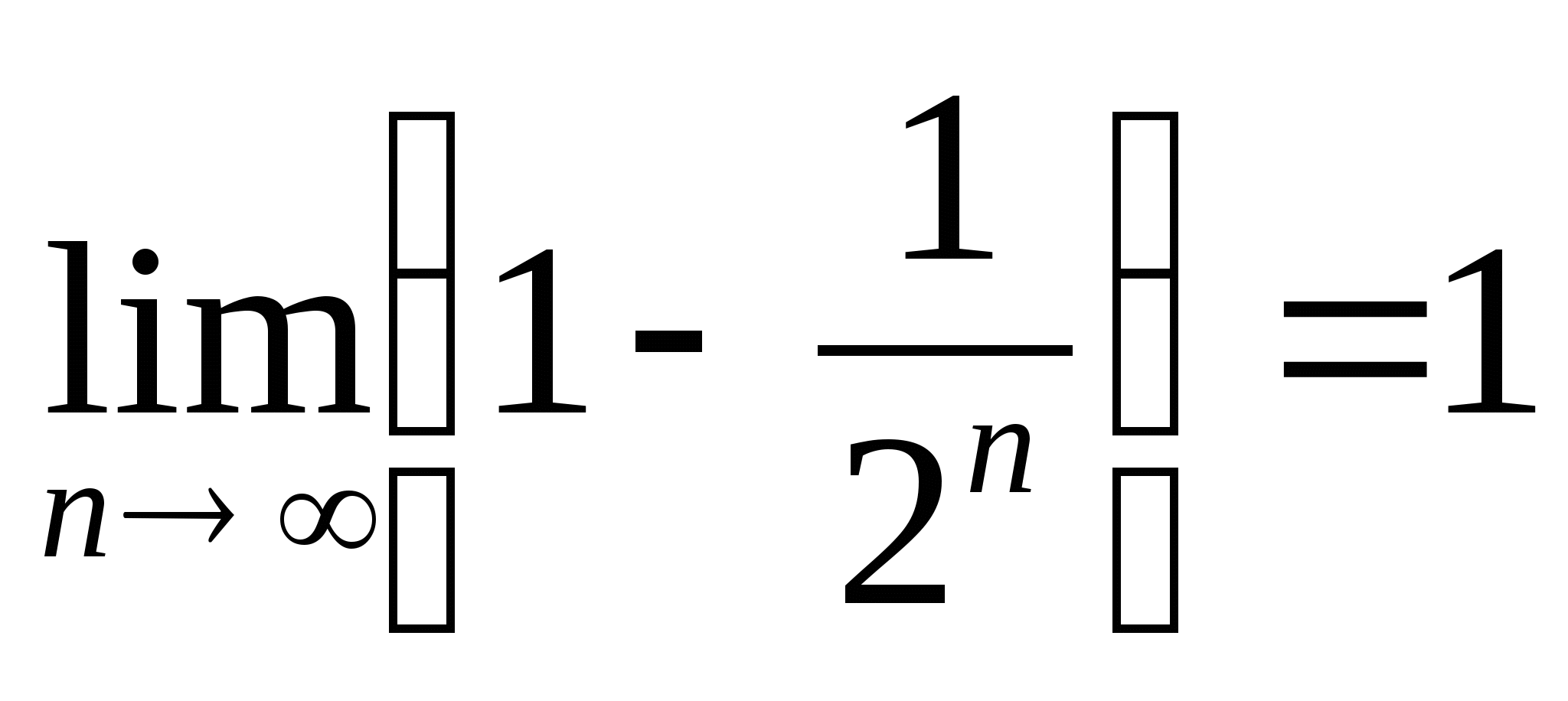 , т.е.
, т.е. 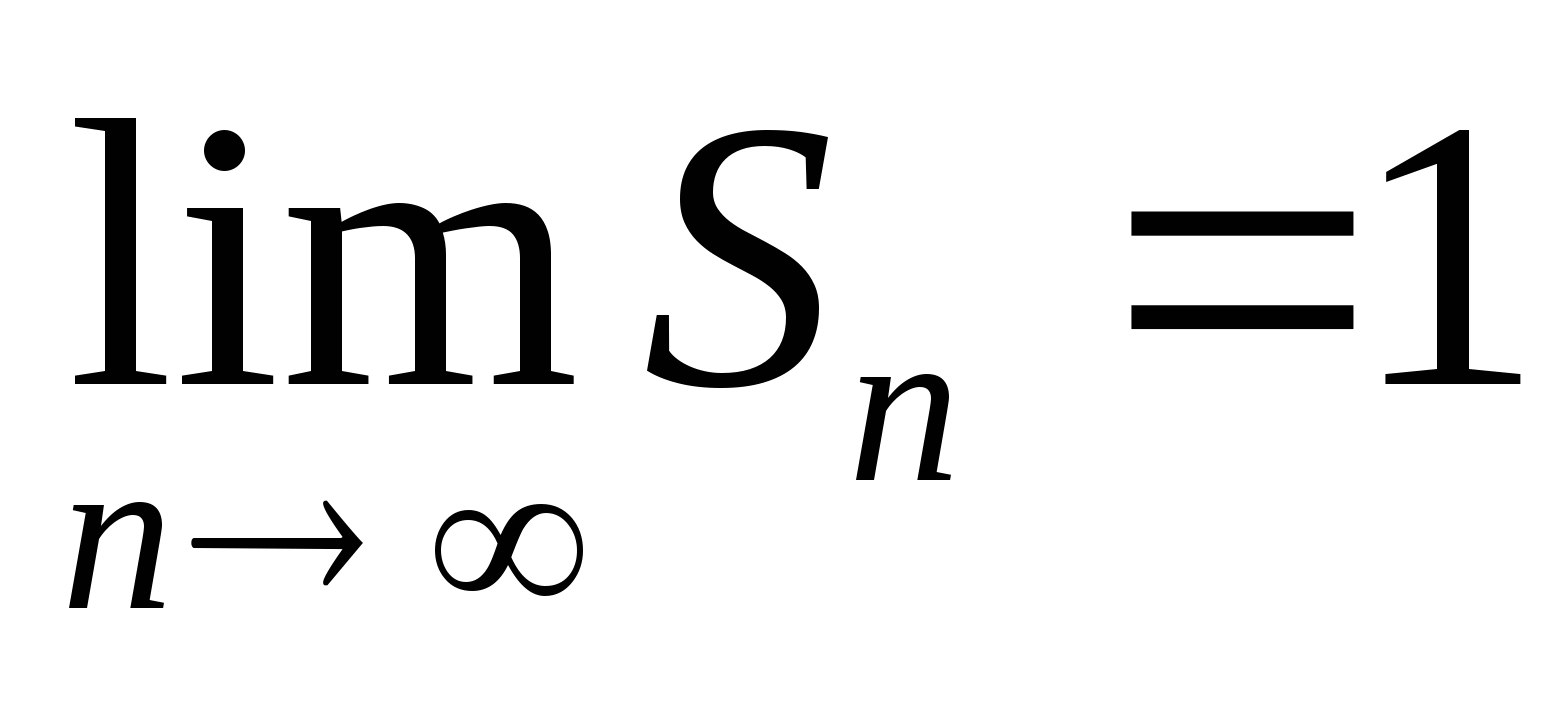 .
.
Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности S1, S2, S3, …, Sn, … .
Например, для прогрессии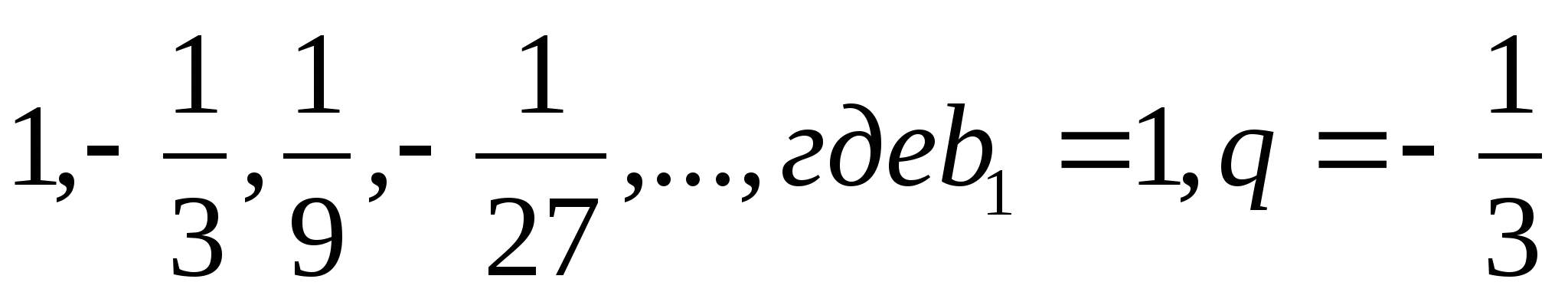 ,
,
имеем
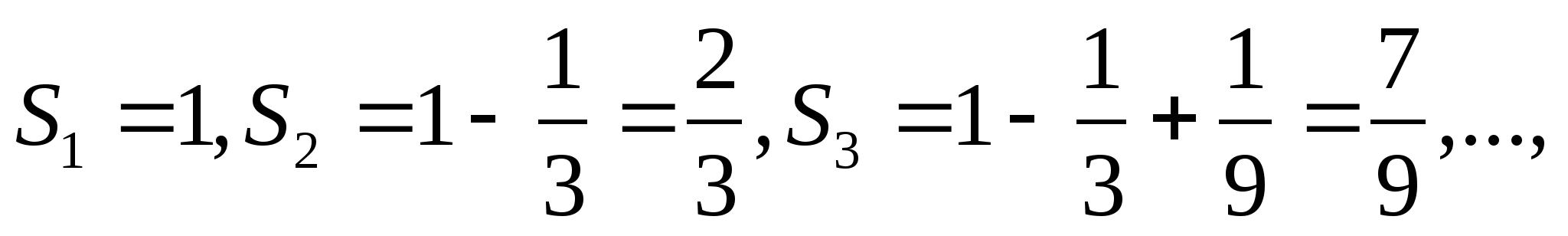
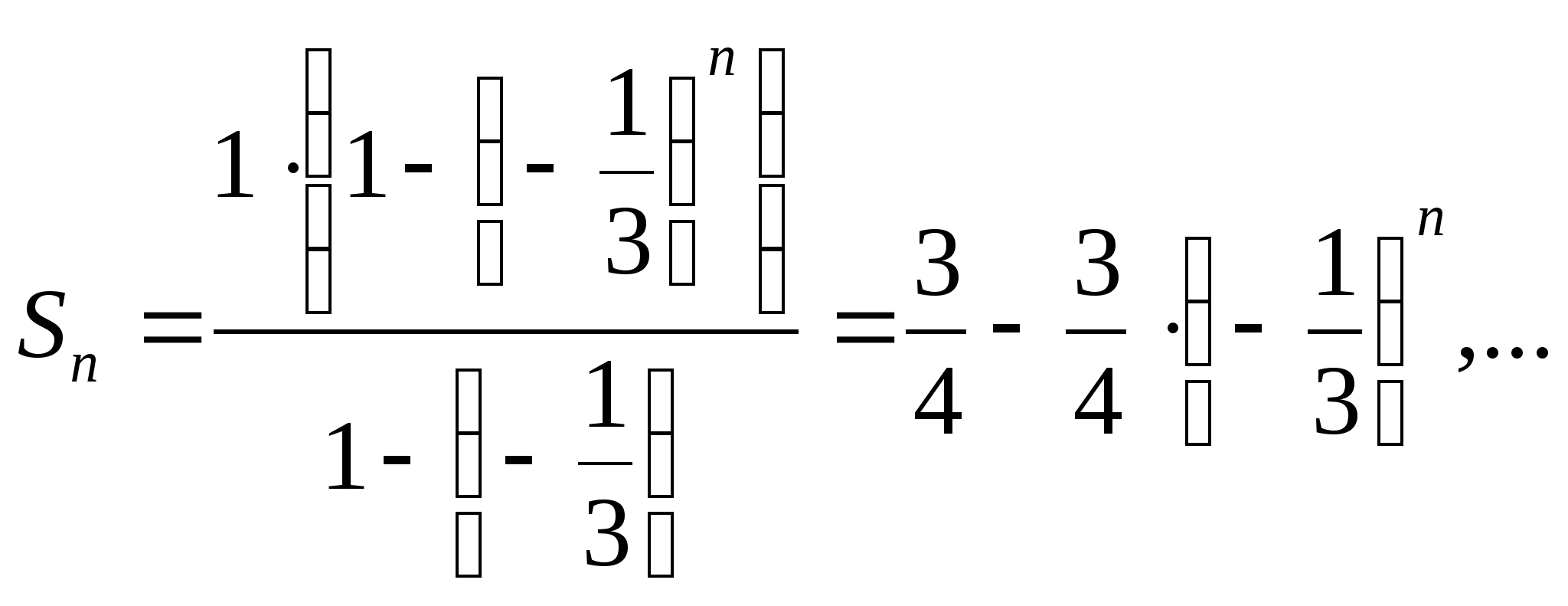 Так как
Так как 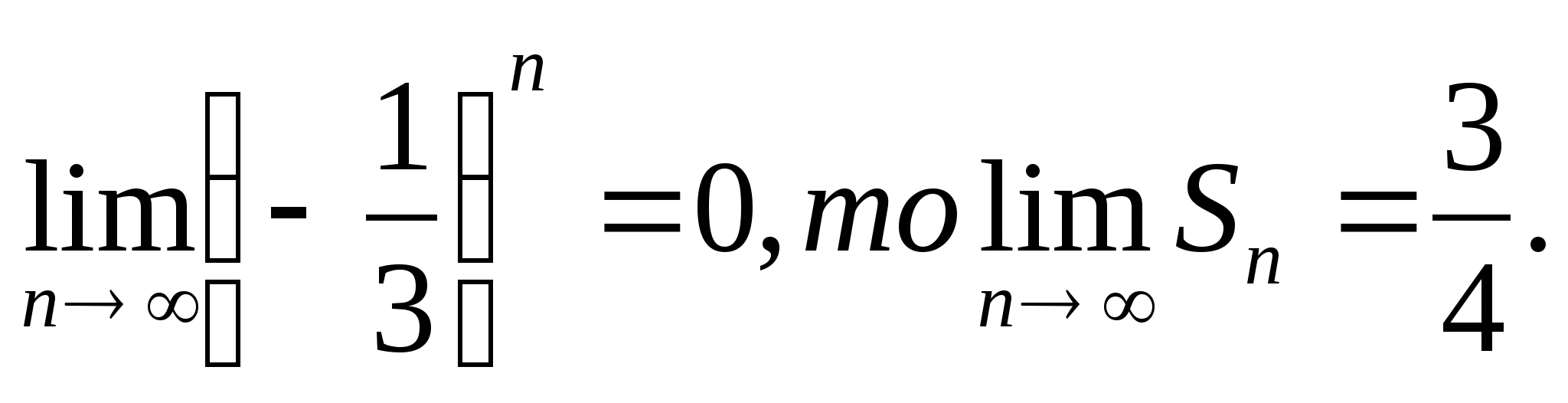
Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле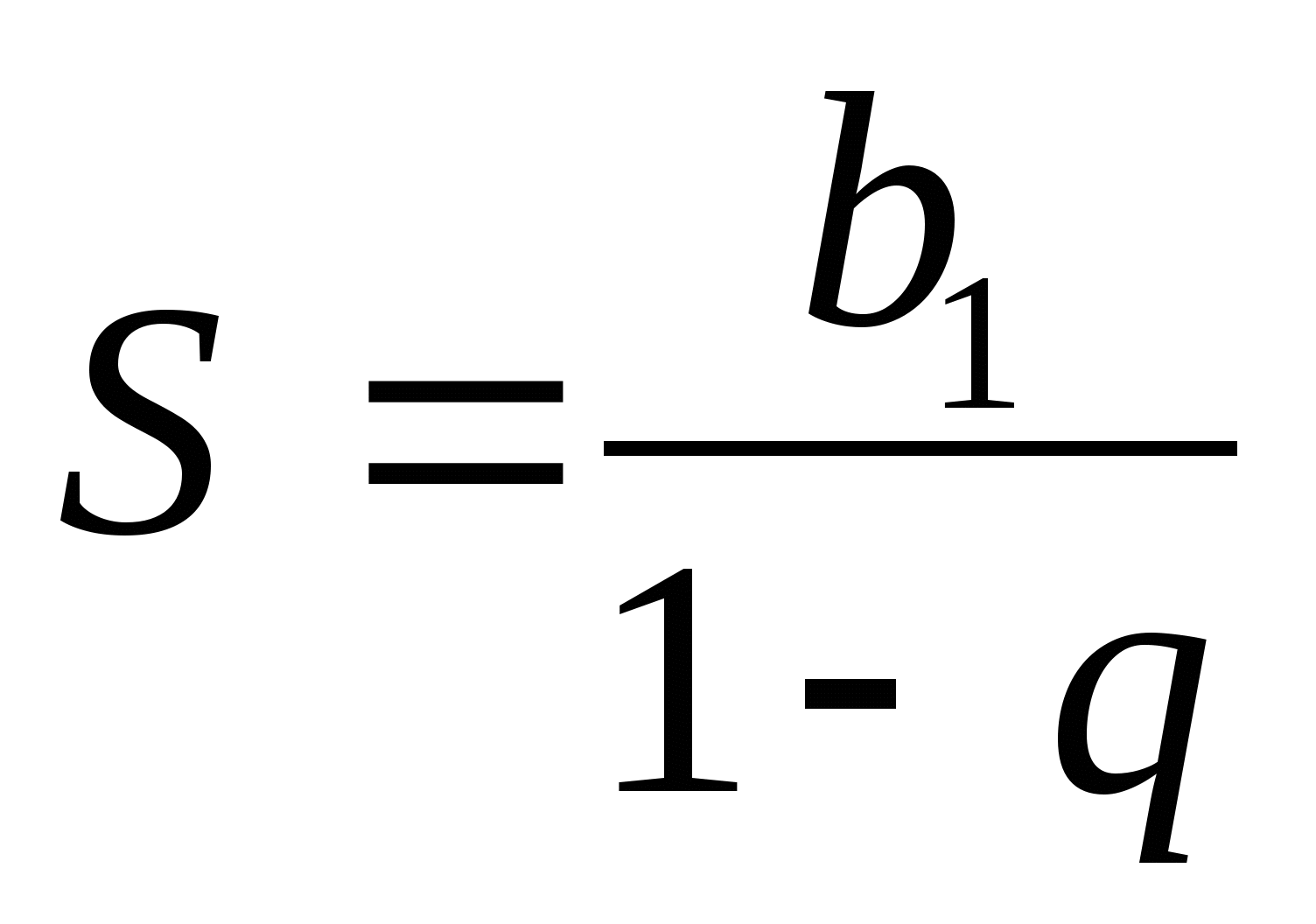 .
.
III. Практическая часть.
№ 16
№ 16 (3)-устно.
№16(4)
№ 17 (1, 3, 4)
№ 20 (3)
№21 (1)
№21 (3)
№22(1)
IV. Подведение итогов.
С какой последовательностью сегодня познакомились?
Дайте определение бесконечно убывающей геометрической прогрессии.
Как доказать, что геометрическая прогрессия является бесконечно убывающей?
Назовите формулу суммы бесконечно убывающей геометрической прогрессии.
Домашнее задание: № 16 (2), № 17 (2), № 21 (2,), № 22 (2), № 23 (2).
Математика 10 класс Дата ___________
Тема: БЕСКОНЕЧНО УБЫВАЮЩАЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Цели:
1) знать формулу суммы бесконечно убывающей геометрической прогрессии, уметь применять эту формулу при решении задач, в частности при записи бесконечной периодической десятичной дроби в виде обыкновенной.
2) Развивать мышление, умение анализировать и делать выводы
3) Воспитывать чувство коллективизма, умение работать в парах
Ход урока
I. Организационный момент.
Проверка домашнего задания
II. Практическая часть.
Работа организована индивидуально у доски и в тетрадях с дифференцированной степенью самостоятельности. Критерием достижения положительного результата этапа является знание всеми учащимися алгоритма нахождения суммы БУГП. Коррекция осуществляется с помощью взаимопроверки. Используются упражнения
18(1,2) Найти сумму БУГП:
1.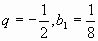 Ответ:
Ответ: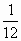
2.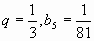
, Ответ: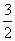
а также упражнения из дидактических материалов по алгебре и началам анализа Б.Г.Зива и В.А. Гольдича, с/р №2, упражнения 1 из вариантов 1 и 2.
Найти сумму БУГП:
1.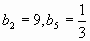 Ответ: 40,5
Ответ: 40,5
2.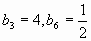 Ответ: 32.
Ответ: 32.
Желающим, справившимся с общим заданием раньше других, предлагается обратная задача:
Известна сумма БУГП и второй член прогрессии. Нужно найти первый член прогрессии и знаменатель:
дано: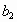 =-0,5; S=1,6;
=-0,5; S=1,6;
найти q и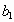 .
.
За самостоятельное решение этой задачи выставляется отдельная оценка.
5 этап. Первичное обобщение и включение нового знания в систему субъектного опыта учащихся.
Установление содержательных взаимосвязей БУГП с линиями уравнений и действительных чисел.
Фронтально решается задача распознавания БГУП. С помощью этой задачи, с одной стороны, осуществляется диагностика достижения положительного результата предыдущих этапов урока, с другой стороны, полученные результаты позволяют осуществить содержательные взаимосвязи по выше указанным линиям.
Из предложенных последовательностей выбрать БУГП:
1)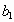 =3; q=2.
=3; q=2.
2)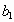 =-4; q=
=-4; q=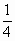 .
.
3) 4;2;1; и т.д.;
4)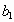 =1; q=x; x>2;
=1; q=x; x>2;
5)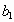 =
=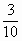 ; q=
; q=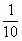 .
.
6)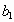
=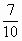 ; q=
; q= .
.
7) =
=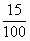 ; q=
; q=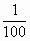
8) =1; q=x; ¦x¦<1.
=1; q=x; ¦x¦<1.
Таковыми являются 2); 3); 5); 6); 7) и 8).
Сначала найдём сумму БУГП из задания 8). Для этого запишем сумму членов прогрессии и воспользуемся формулой суммы БУГП. Получим:
1+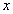 +
+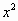 + …+
+ …+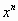 + …=
+ …= 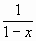 .
.
Установление содержательных взаимосвязей БУГП с линией уравнений
Сравните полученный результат с уравнением и воспользуйтесь при его решении полученным результатом:
Уравнение 1)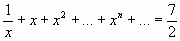 ; ¦x¦<1.
; ¦x¦<1.
Заметим, что если к обеим частям равенства прибавить 1, то можно воспользоваться полученным выше результатом:
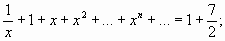
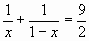 .
.
Итак, мы получили дробное рациональное уравнение, алгоритм решения которого известен школьникам.
Уравнение 2) 2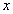 + 1 +
+ 1 +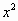 -
- 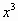 +
+ 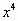
-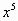 + …=
+ …= 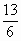
¦x¦<1.
Решение уравнения 1) проводится учеником на доске, уравнение 2 предлагается для самостоятельной работы дома.
Делается весьма неожиданный вывод о том, что сумма БГУП даёт возможность решения некоторых уравнений, имеющих бесконечное число членов.
Таким образом, удаётся установить содержательную связь БУГП с линией уравнений.
Установление содержательных взаимосвязей БУГП с линией действительных чисел.
К доске приглашаются 3 ученика для решения задач 1-3.
1) =
= ; q=
; q= .
.
Сначала находим сумму БУГП по формуле
S=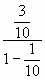 =
=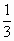 .
.
Затем попытаемся осмыслить, что представляет собой сумма членов этой прогрессии, если её члены записать в виде десятичных дробей:
0,3+0,03+0,003+….=0,3333…=0,(3).
Таким образом, видим, что с помощью формулы суммы БУГП можно осуществлять переход от записи действительного числа в виде бесконечной периодической дроби к записи в виде обыкновенной дроби.
2) =
= ; q=
; q= .
.
Эта задача носит дублирующий характер и используется для создания условий лучшего осмысления сформулированного вывода.
3) =
=
данная геометрическая прогрессия является бесконечно убывающей.
б) данная последовательность не является бесконечно убывающей геометрической прогрессией.
Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию:
Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.
Но в левой части этого равенства – сумма бесконечного числа слагаемых.
Рассмотрим сумму n первых слагаемых.
По формуле суммы n первых членов геометрической прогрессии, она равна
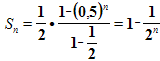 .
.Если n неограниченно возрастает, то
или
Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности S1, S2, S3, …, Sn, … .
Например, для прогрессии
имеем
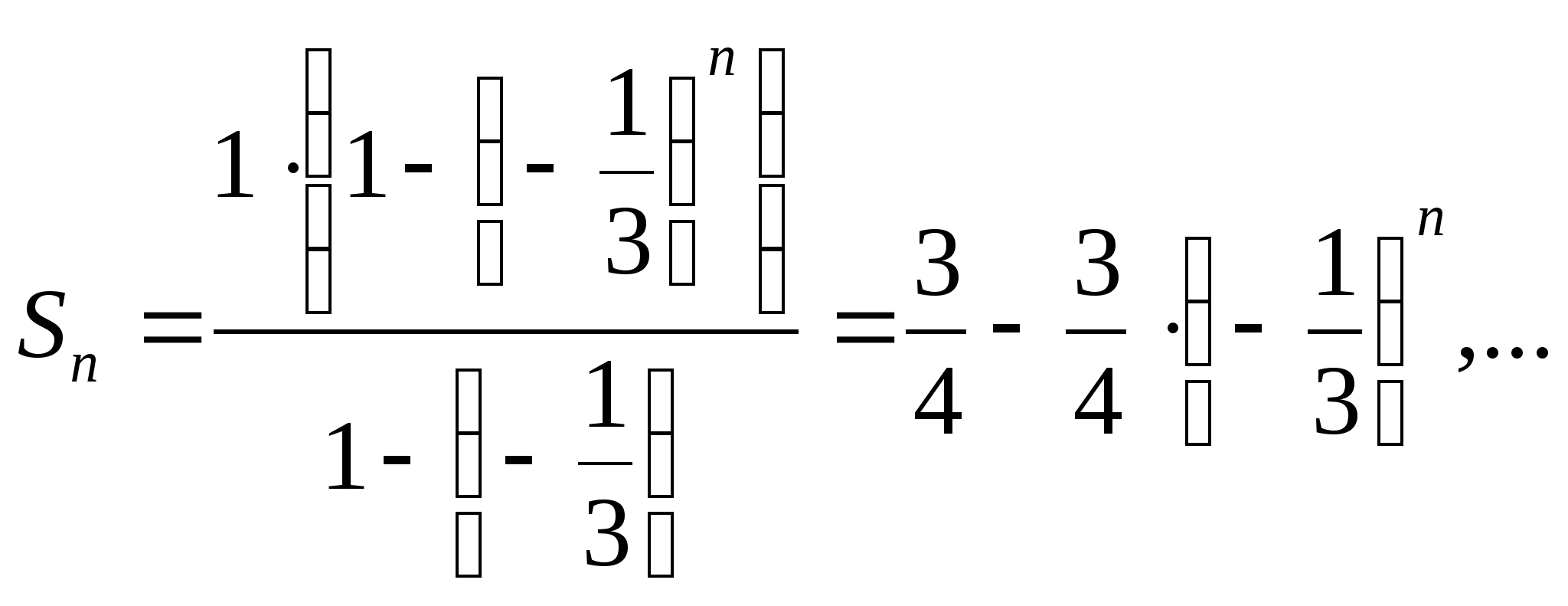 Так как
Так как Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле
III. Практическая часть.
№ 16
№ 16 (3)-устно.
№16(4)
№ 17 (1, 3, 4)
№ 20 (3)
№21 (1)
№21 (3)
№22(1)
IV. Подведение итогов.
С какой последовательностью сегодня познакомились?
Дайте определение бесконечно убывающей геометрической прогрессии.
Как доказать, что геометрическая прогрессия является бесконечно убывающей?
Назовите формулу суммы бесконечно убывающей геометрической прогрессии.
Домашнее задание: № 16 (2), № 17 (2), № 21 (2,), № 22 (2), № 23 (2).
Математика 10 класс Дата ___________
Тема: БЕСКОНЕЧНО УБЫВАЮЩАЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Цели:
1) знать формулу суммы бесконечно убывающей геометрической прогрессии, уметь применять эту формулу при решении задач, в частности при записи бесконечной периодической десятичной дроби в виде обыкновенной.
2) Развивать мышление, умение анализировать и делать выводы
3) Воспитывать чувство коллективизма, умение работать в парах
Ход урока
I. Организационный момент.
Проверка домашнего задания
II. Практическая часть.
Работа организована индивидуально у доски и в тетрадях с дифференцированной степенью самостоятельности. Критерием достижения положительного результата этапа является знание всеми учащимися алгоритма нахождения суммы БУГП. Коррекция осуществляется с помощью взаимопроверки. Используются упражнения
18(1,2) Найти сумму БУГП:
1.
2.
, Ответ:
а также упражнения из дидактических материалов по алгебре и началам анализа Б.Г.Зива и В.А. Гольдича, с/р №2, упражнения 1 из вариантов 1 и 2.
Найти сумму БУГП:
1.
2.
Желающим, справившимся с общим заданием раньше других, предлагается обратная задача:
Известна сумма БУГП и второй член прогрессии. Нужно найти первый член прогрессии и знаменатель:
дано:
найти q и
За самостоятельное решение этой задачи выставляется отдельная оценка.
5 этап. Первичное обобщение и включение нового знания в систему субъектного опыта учащихся.
Установление содержательных взаимосвязей БУГП с линиями уравнений и действительных чисел.
Фронтально решается задача распознавания БГУП. С помощью этой задачи, с одной стороны, осуществляется диагностика достижения положительного результата предыдущих этапов урока, с другой стороны, полученные результаты позволяют осуществить содержательные взаимосвязи по выше указанным линиям.
Из предложенных последовательностей выбрать БУГП:
1)
2)
3) 4;2;1; и т.д.;
4)
5)
6)
=
7)
8)
Таковыми являются 2); 3); 5); 6); 7) и 8).
Сначала найдём сумму БУГП из задания 8). Для этого запишем сумму членов прогрессии и воспользуемся формулой суммы БУГП. Получим:
1+
Установление содержательных взаимосвязей БУГП с линией уравнений
Сравните полученный результат с уравнением и воспользуйтесь при его решении полученным результатом:
Уравнение 1)
Заметим, что если к обеим частям равенства прибавить 1, то можно воспользоваться полученным выше результатом:
Итак, мы получили дробное рациональное уравнение, алгоритм решения которого известен школьникам.
Уравнение 2) 2
-
¦x¦<1.
Решение уравнения 1) проводится учеником на доске, уравнение 2 предлагается для самостоятельной работы дома.
Делается весьма неожиданный вывод о том, что сумма БГУП даёт возможность решения некоторых уравнений, имеющих бесконечное число членов.
Таким образом, удаётся установить содержательную связь БУГП с линией уравнений.
Установление содержательных взаимосвязей БУГП с линией действительных чисел.
К доске приглашаются 3 ученика для решения задач 1-3.
1)
Сначала находим сумму БУГП по формуле
S=
Затем попытаемся осмыслить, что представляет собой сумма членов этой прогрессии, если её члены записать в виде десятичных дробей:
0,3+0,03+0,003+….=0,3333…=0,(3).
Таким образом, видим, что с помощью формулы суммы БУГП можно осуществлять переход от записи действительного числа в виде бесконечной периодической дроби к записи в виде обыкновенной дроби.
2)
Эта задача носит дублирующий характер и используется для создания условий лучшего осмысления сформулированного вывода.
3)