Ещё пример задания:

Р-25. (демо-2021) Значение арифметического выражения: 49⁷ + 7²¹ – 7 – записали в системесчисления с основанием 7. Сколько цифр 6 содержится в этой записи?Решение:

1. 
   приведём все числа к степеням семерки, учитывая, что 49 = 7²
   

7¹⁴ + 7²¹ – 7¹

2. 
   расставим степени в порядке убывания:
   

7²¹ + 7¹⁴ – 7¹

3. 
   Очевидно, что «шестёрки» в семеричной записи значения выражения возникнут только за счёт вычисления разности 7¹⁴ – 7¹, их количество равно 14-1=13
   
4. 
   Ответ: 13.
   

Решение (использование программы):

1. 
   язык Python позволяет работать с большими числами, не задумываясь о том, что для их хранения требуется больше памяти, чем для «обычного» целого числа (когда значение не помещается в 4 байта, интерпретатор автоматически переходит на представление числа в виде массива с «длинной арифметикой»)
   
2. 
   поэтому может быть написана программа, которая вычисляет нужное значение и методом деления в столбик определяет все цифры его записи в семеричной системе счисления; шестёрки считаем с помощью счётчика count6:
   

x = 49**7 + 7**21 - 7count6 = 0while x:if x % 7 == 6: count6 += 1x //= 7print( count6 )

3. 
   Ответ: 13.
   

Решение (использование программы в среде PascalABC.NET, А. Агафонцев):

1. 
   Pascal ABC.NET за счет использования фреймворка .NET позволяет воспользоваться типом System.Numerics.BigInteger (предназначенным для произвольно больших целых со знаком) и связанными с ним функциями.
   
2. 
   Таким образом, программа получается во многом схожей с программами на Python. Особо отметим, что использование функций возведения в степень не связанных с типом BigInteger для систем с основанием, не являющимся степенью двойки, приводит к неверным результатам из-за использования вещественных чисел. Например, BigInteger(power(9,34)) или BigInteger(9 ** 34) преобразуют вещественное число в целое произвольно большой длины, но еще при операции возведения в степень потеряется часть идеальной, математической мантиссы.
   
3. 
   В связи с вышесказанным допустимо только использование записей вида BigInteger.Pow(9,34).
   
4. 
   Полная программа:
   

---

vara: BigInteger;k: int64;begina := BigInteger.Pow(49, 7) + BigInteger.Pow(7, 21) - 7;k := 0;while (a > 0) dobeginif (a mod 7 = 6) thenk := k + 1;a := a div 7;end;writeln(k);end.

5. 
   Ещё одно решение на PascalABC.NET (П.Е. Финкель)
   

beginvar k:=0;var x:=49bi**7+7bi**21-7;while x>0 do beginif x mod 7=6 then k+=1;x:=x div 7;end;println(k);end.

6. 
   здесь «bi» длинным, а ** означает возведение в степень
   
7. 
   Ответ: 13.
   

Решение (использование программы на Java, М. Коротков):

1. 
   язык Java позволяет работать с большими числами с помощью типа BigInteger;
   
2. 
   может быть написана программа, которая вычисляет значение арифметического выражения и методом деления в столбик определяет все цифры его записи в семеричной системе счисления; шестёрки считаем с помощью счётчика amt6:
   
3. 
   полная программа:
   

import java.math.BigInteger;
public class Main {
public static void main(String[] args) {
final BigInteger SIX = BigInteger.valueOf(6);
final BigInteger SEVEN = BigInteger.valueOf(7);
final BigInteger NUM1 = BigInteger.valueOf(49).pow(7);
final BigInteger NUM2 = BigInteger.valueOf(7).pow(21);

BigInteger num = NUM1.add(NUM2).subtract(SEVEN); BigInteger amt6 = BigInteger.ZERO;
while (!num.equals(BigInteger.ZERO)) {
if (num.mod(SEVEN).equals(SIX)) {
amt6 = amt6.add(BigInteger.ONE);
}
num = num.divide(SEVEN);
}
System.out.println(amt6);
}
}

4. 
   Ответ: 13.
   

---

Ещё пример задания:

Р-24. (М.В. Кузнецова) Значение арифметического выражения: 64¹⁰ + 2⁹⁰ - 16 записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи?Решение:

1. 
   Приведём все числа к степеням восьмерки, учитывая, что 16 = 64 - 48 =8²-6∙8¹
   

64¹⁰ + 2⁹⁰ - 16 = (8²)¹⁰ + 2^3∙30– (8² – 48) = 8²⁰ + 8³⁰– 8² + 6∙8¹

2. 
   Перепишем выражение, располагая степени восьмёрки в порядке убывания:
   8²⁰ + 8³⁰ – 8² + 6∙8¹ = 8³⁰ + 8²⁰ – 8² + 6∙8¹
   
3. 
   Очевидно, что «семёрки» в восьмеричной записи значения выражения возникнут только за счёт вычисления разности 8²⁰ – 8², их количество равно 20-2=18
   
4. 
   Ответ: 18.
   

Решение (использование программы в среде PascalABC.NET, А. Агафонцев):

1. 
   В среде Pascal ABC.NET при использовании типа BigInteger задача может быть решена с помощью программы:
   

vara: BigInteger;k: int64;begina := BigInteger.Pow(64, 10) + BigInteger.Pow(2, 90) - 16;k := 0;while (a > 0) dobeginif (a mod 8 = 7) thenk := k + 1;a := a div 8;end;writeln(k);end.

2. 
   Ответ: 18.
   
3. 
   Ещё одно решение на PascalABC.NET (П.Е. Финкель)
   

beginvar k:=0;var x:=64bi**10+2bi**90-16;while x>0 do beginif x mod 8=7 then k+=1;x:=x div 8;end;println(k);end.Решение (программа на Python, Б.С. Михлин):

1. 
   если доступна среда программирования на Python, можно написать программу, которая использует встроенную арифметику длинных чисел:
   

x = 64**10 + 2**90 - 16print( oct(x).count('7') )

2. 
   ответ: 18.
   

Ещё пример задания:

Р-23. (М.В. Кузнецова) Значение арифметического выражения: 9⁹ – 3⁹ + 9¹⁹ – 19 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?Решение:

1. 
   Приведём все числа к степеням тройки, учитывая, что 19=27-8=3³-(2∙3¹+2∙3⁰):
   

---

9⁹ – 3⁹ + 9¹⁹ – 19= (3²)⁹ – 3⁹ + (3²)¹⁹ – (3³ – (2∙3¹ + 2∙3⁰)) = 3¹⁸ – 3⁹ + 3³⁸ – 3³ + 2∙3¹ + 2∙3⁰

2. 
   Перепишем выражение, располагая степени тройки в порядке убывания:
   3¹⁸ – 3⁹ + 3³⁸ – 3³ + 2∙3¹ + 2∙3⁰ = 3³⁸ + 3¹⁸ – 3⁹ – 3³ + 2∙3¹ + 2∙3⁰
   
3. 
   Сначала рассмотрим часть выражения, в которой имеется два расположенных подряд «минуса»: 3¹⁸ - 3⁹ ‑ 3³:
   
   1. 
      найдём разность двух крайних чисел: 3¹⁸ – 3³, в её троичной записи 18 – 3=15 «двоек» и 3 «нуля»;
      
   2. 
      вычтем из этого числа значение 3⁹: одна из «двоек» (на 10-й справа позиции) уменьшится на 1, остальные цифры не изменятся;
      
   3. 
      итак, троичная запись разности 3¹⁸ – 3⁹ – 3³ содержит 15 – 1=14 «двоек», одну «единицу» и 3 «нуля»
      
4. 
   Прибавим к полученному значению сумму: 2∙3¹ + 2∙3⁰ = 22₃. В троичной записи результата два крайних справа нуля заменяются на «двойки», остаётся один ноль. Общее количество «двоек»: 14+2=16.
   
5. 
   Прибавление значения 3³⁸ не изменит количества «двоек» в троичном числе: слева от имеющихся цифр появятся ещё 38 – 18=20 «нулей» и одна «единица» – на 39-й справа позиции.
   
6. 
   Итак, результат, записанный в троичной системе, содержит 39 цифр. Его состав: 16 «двоек», 2 «единицы» (их позиции: 39-я и 10-я справа) и 21 «нуль» (39-16-2=21).
   
7. 
   Ответ: 16.
   

---

Ещё пример задания:

Р-22. Значение арифметического выражения: 9⁸ + 3⁵ – 9записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?Решение:

1. 
   приведём все слагаемые к виду 3^N и расставим в порядке убывания степеней:
   

9⁸ + 3⁵ – 9 = 3¹⁶ + 3⁵ – 3²

2. 
   первое слагаемое, 3¹⁶, даёт в троичной записи одну единицу – она нас не интересует
   
3. 
   пара 3⁵ – 3² даёт 5 – 2 = 3 двойки
   
4. 
   Ответ: 3.
   

Решение (программа, Б.С. Михлин):

1. 
   задача может быть решена с помощью программы на Python, где есть встроенная поддержка длинных чисел:
   

x = 9**8+3**5-9x3 = ''while x:x3 = str(x%3) + x3x //= 3print( 'Ответ:', x3.count('2') )

2. 
   вариант без использования символьных строк:
   

x = 9**8+3**5-9count2 = 0while x:if x % 3 == 2:count2 += 1x //= 3print( 'Ответ:', count2 )

3. 
   Ответ: 3.
   

Решение (электронные таблицы, Б.С. Михлин):

1. 
   эта конкретная задача может быть решена с помощью электронных таблиц
   
2. 
   Замечание. Электронные таблицы имеют ограничения при работе с длинными целыми числами. Например, Excel при вводе больших чисел заменяет все цифры после 15-го разряда на нули. Это легко проверить, введя в ячейку число с более чем 15-ю разрядами.
   

Обычно электронные таблицы при этом переходят к экспоненциальному (научному) формату. Если число больше, чем 10¹⁵, то оно хранится как вещественное число (неточно). Это ограничивает использование электронных таблиц. В этой задаче заданное число меньше, чем 10¹⁵, поэтому использовать электронные таблицы можно.

3. 
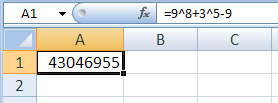
   введём заданное число, заданное арифметическим выражением, в ячейку электронной таблицы:
   

4. 
   выполним алгоритм перевода числа в троичную систему: найдём в B1 остаток от деления числа на 3, а в A2 – частное:
   

---

Смотрите также файлы

• Дневник производственной практики пм. 04 Выполнение работ по профессии Младшая медицинская сестра по уходу за больными.docx

• Немного предыстории и истории Power bi.pdf

• Противодействие коррупции любых стран.docx

• Сценарий 9 мая 2023 года.docx

• Методические рекомендации по организации выполнения и защиты дипломного проекта (работы) по программам подготовки специалистов среднего звена.docx