ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 1060
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
+ (23)800 – 22 – 21 = 24032 – 22018 + 22400 – 26 – 24
24032 + 22400 – 22018 – 26 – 24
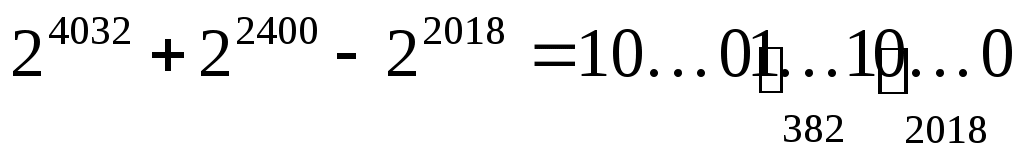
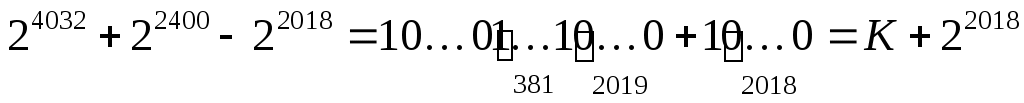 ,
,
где число K содержит 382 единицы в старших разрядах; таки образом, интересующее нас число равно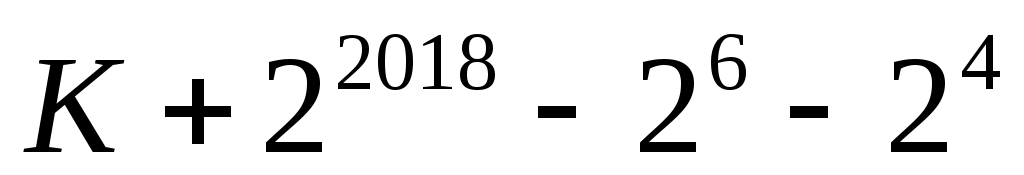
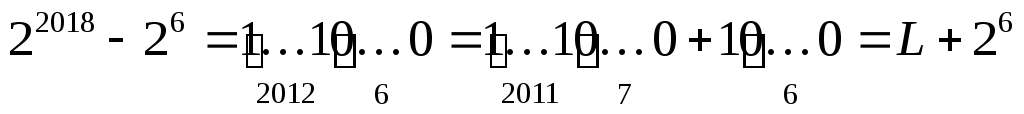
где число L содержит 2011 единиц
Решение (способ 2, Е.А. Смирнов, Нижегородская область):
42016 – 22018 + 8800 – 80 = (22)2016 – 22018 + (23)800 – 22 – 21 = 24032 – 22018 + 22400 – 26 – 24
24032 + 22400 – 22018 – 26 – 24
24032 + 22400 – 22019 + 22018 – 27 + 26– 24
ответ: 2395
Решение (способ 3, А.И. Козлов, г. Северобайкальск):
42016 – 22018 + 8800 – 80 = (22)2016 – 22018 + (23)800 – 22 – 21 = 24032 – 22018 + 22400 – 26 – 24
24032 + 22400 – 22018 – 26 – 24
Р-15. Решите уравнение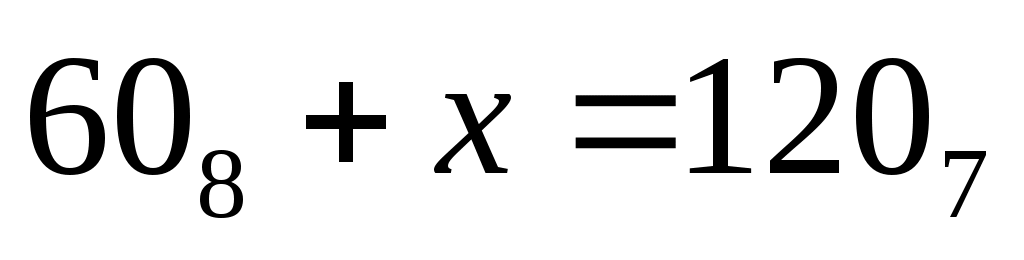 .
.
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
Решение:
Решение (программа на Python, А.Н. Носкин):
a = int('60', 8 ) # перевод "60" в 10-ю систему
b = int('120', 7 ) # перевод "120" в 10-ю систему
x = b - a # число Х в 10-й системе
x6 = ''
while x > 0:# перевод в 6-ю систему
x6 += str(x%6)
x //= 6
x6 = x6[::-1]# разворот числа
print(x6)
x = int( '120', 7 ) - int( '60', 8 )
print('в 10 c.c:', x)
s = ''
while x:
s = str( x%6 ) + s
x //= 6
print( 'Ответ в 6 с.с:', s )
Р-14. Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Решение:
Решение (программа на Python, А.Н. Носкин):
for i in range(1,100):
x = i
x3 = ''
while x > 0:# перевод в 3-ю систему
x3 += str(x%3)
x //= 3
x3 = x3[::-1][-1]# последняя цифра числа
x = i
x5 = ''
while x > 0:
x5 += str(x%5)
x //= 5
x5 = x5[::-1][-1]
if x3 == "0" and x5 == "0":
print(i)
break
Решение (программа на Python, Б.С. Михлин):
for x in range(1,101): # ищем решение от 1 до 100
if x%3 == x%5 == 0: # 'and' можно не использовать
print(x)
break
Р-13. Запись числа 6710 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Укажите основание этой системы счисления N.
Решение:
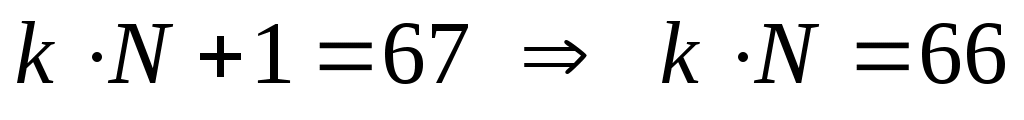
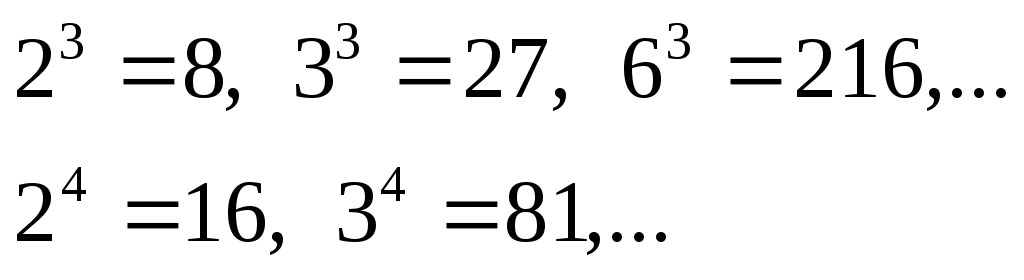
Решение (программа на Python, А.Н. Носкин):
for i in range(2,37):# перебираем возможные основания
x = 67
x_N = ''
while x > 0:# перевод в N-ю систему
x_N += str(x%i)
x //= i
x_N = x_N[::-1]# разворот числа
if x_N[-1]== "1" and len(x_N) == 4:
print(i)
break
Решение (программа на Python, Б.С. Михлин):
for N in range(2, 37): # подбираем основание от 2 до 36
x = 67
s = '' # в s будет представление числа в N-ичной системе
while x:
d = x % N # цифра (digit)
if d < 10:
d = str( d ) # цифра от 0 до 9
else:
d = chr( ord( 'A' ) + d - 10 ) # «цифра» от A до Z
s = d + s # цифру d приписываем слева к s
x //= N
if s[-1] == '1' and len( s ) == 4:
print( N )
break
for N in range(2, 101): # подбираем основание от 2 до 100
x = 67
k = 0 # счетчик цифр (разрядов) N-ичного числа
while x:
d = x % N # очередная цифра (digit)
k += 1
if k == 1: d0 = d # d0 - младшая цифра
x //= N
if d0 == 1 and k == 4:
print( N )
break
-
перестроим слагаемые в порядке уменьшения степеней двойки
24032 + 22400 – 22018 – 26 – 24
-
вспомним, что число 2N-1 в двоичной системе записывается как N единиц: ,
,
а число 2N–2K при K < N записывается как N–K единиц и K нулей:
-
согласно п. 2, число 22400 – 22018 запишется как 382 единицы и 2018 нулей -
добавляем старшее слагаемое 24032, получаем число 24032 + 22400 – 22018, в котором 383 единицы и в конце (после последней единицы) – 2018 нулей:
-
выделим из этого значения последнюю единицу со следующими 2018 нулями как отдельное слагаемое (число 22018):
где число K содержит 382 единицы в старших разрядах; таки образом, интересующее нас число равно
-
согласно п. 2, число 22018 – 26 запишется как 2012 единиц и 6 нулей; также выделим последнюю единицу с последующими нулями как отдельное слагаемое:
где число L содержит 2011 единиц
-
теперь остаётся найти, сколько единиц будет в двоичной записи числа 26 – 24, согласно п. 2 находим, что оно содержит 2 единицы -
таким образом, общее число единиц равно 382 + 2011 + 2 = 2395 -
ответ: 2395.
Решение (способ 2, Е.А. Смирнов, Нижегородская область):
-
приведём все числа к степеням двойки, разложив 80 как 26+24
42016 – 22018 + 8800 – 80 = (22)2016 – 22018 + (23)800 – 22 – 21 = 24032 – 22018 + 22400 – 26 – 24
-
перестроим слагаемые в порядке уменьшения степеней двойки
24032 + 22400 – 22018 – 26 – 24
-
представим – 22018 = – 22019 + 22018 и – 26 = – 27 + 26
24032 + 22400 – 22019 + 22018 – 27 + 26– 24
-
слагаемое 24032 в двоичной записи содержит 1 единицу -
слагаемое 22400 – 22019 содержит 381 единицу (число 2N–2K при K < N в двоичной системе записывается как N–K единиц и K нулей: )
) -
слагаемое 22018 – 27 содержит 2011 единиц, слагаемое 26– 24 содержит 2 единицы -
позиции единиц во всех этих слагаемых не совпадают, поэтому общее количество единиц равно 1 + 381 + 2011 + 2 = 2395
ответ: 2395
Решение (способ 3, А.И. Козлов, г. Северобайкальск):
-
приведём все числа к степеням двойки, разложив 80 как 26+24
42016 – 22018 + 8800 – 80 = (22)2016 – 22018 + (23)800 – 22 – 21 = 24032 – 22018 + 22400 – 26 – 24
-
перестроим слагаемые в порядке уменьшения степеней двойки
24032 + 22400 – 22018 – 26 – 24
-
выражение 22400–24 дает 2396 единиц и 4 нолика в конце, откуда вычеркиваем (заменяем на ноль) единичку, стоящую на седьмом месте справа (26) и, соответственно на 2019 месте справа (22018). Следовательно, остается 2394 единички. -
С учетом того, что 24032 дает нам одну единицу, в итоге получаем 2395 единиц -
Ответ: 2395
Ещё пример задания:
Р-15. Решите уравнение
Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
Решение:
-
удобнее всего перевести все числа в десятичную систему, решить уравнение и результат перевести в шестеричную систему -
получаем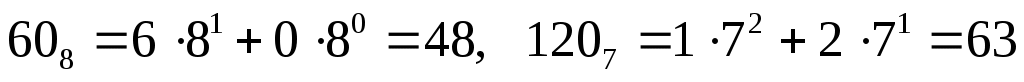
-
уравнение приобретает вид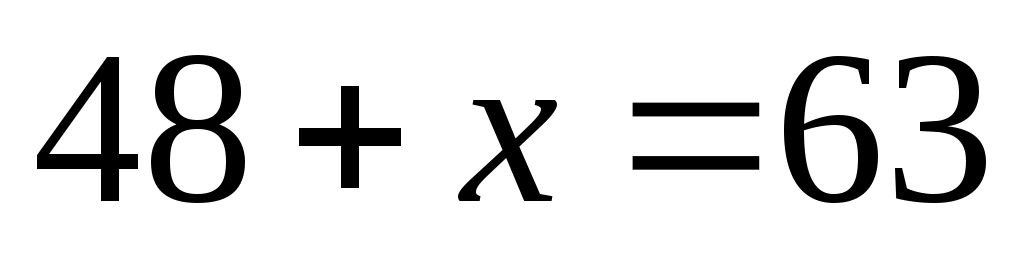 , откуда получаем
, откуда получаем 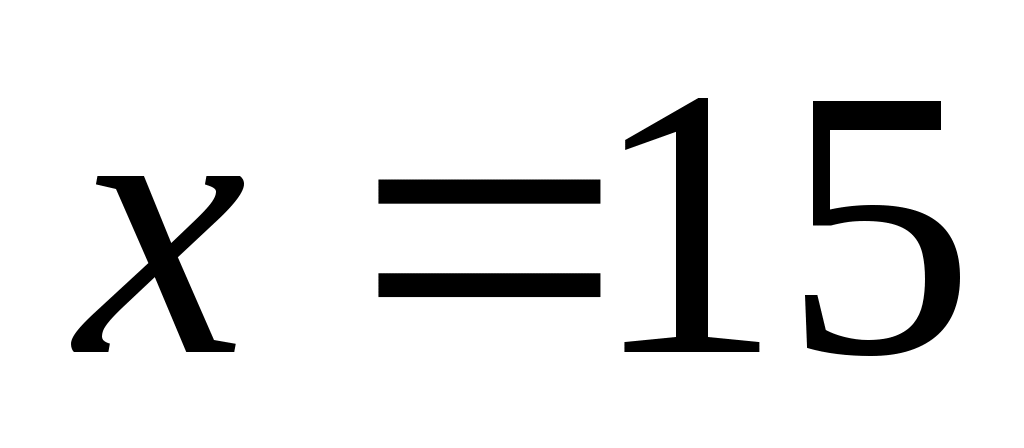
-
переводим 15 в шестеричную систему счисления: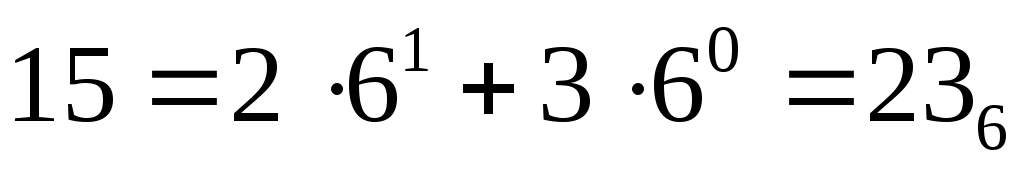
-
ответ: 23.
Решение (программа на Python, А.Н. Носкин):
-
можно (но сложнее) решить задачу с помощью программы:
a = int('60', 8 ) # перевод "60" в 10-ю систему
b = int('120', 7 ) # перевод "120" в 10-ю систему
x = b - a # число Х в 10-й системе
x6 = ''
while x > 0:# перевод в 6-ю систему
x6 += str(x%6)
x //= 6
x6 = x6[::-1]# разворот числа
print(x6)
-
ещё один вариант программы (Б.С. Михлин):
x = int( '120', 7 ) - int( '60', 8 )
print('в 10 c.c:', x)
s = ''
while x:
s = str( x%6 ) + s
x //= 6
print( 'Ответ в 6 с.с:', s )
-
ответ: 23.
Ещё пример задания:
Р-14. Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Решение:
-
если запись числа в системе счисления с основанием N заканчивается на 0, то это число делится на N нацело -
поэтому в данной задаче требуется найти наименьшее натуральное число, которое делится одновременно на 3 и на 5, то есть, делится на 15 -
очевидно, что это число 15.
Решение (программа на Python, А.Н. Носкин):
-
можно (но сложнее) решить задачу с помощью программы:
for i in range(1,100):
x = i
x3 = ''
while x > 0:# перевод в 3-ю систему
x3 += str(x%3)
x //= 3
x3 = x3[::-1][-1]# последняя цифра числа
x = i
x5 = ''
while x > 0:
x5 += str(x%5)
x //= 5
x5 = x5[::-1][-1]
if x3 == "0" and x5 == "0":
print(i)
break
-
ответ: 15.
Решение (программа на Python, Б.С. Михлин):
-
Используется тот факт, что последняя цифра в записи числа в системе счисления с основанием N – это остаток от деления этого числа на N:
for x in range(1,101): # ищем решение от 1 до 100
if x%3 == x%5 == 0: # 'and' можно не использовать
print(x)
break
-
ответ: 15.
Ещё пример задания:
Р-13. Запись числа 6710 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Укажите основание этой системы счисления N.
Решение:
-
поскольку запись в системе счисления с основанием N заканчивается на 1, то остаток от деления числа 67 на N равен 1, то есть при некотором целом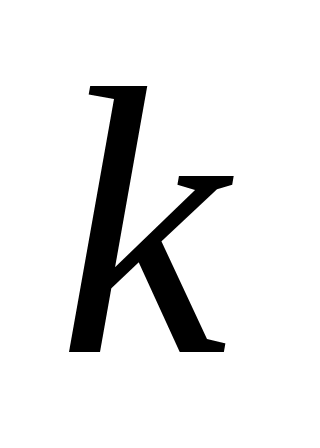 имеем
имеем
-
следовательно, основание N – это делитель числа 66 -
с другой стороны, запись числа содержит 4 цифры, то есть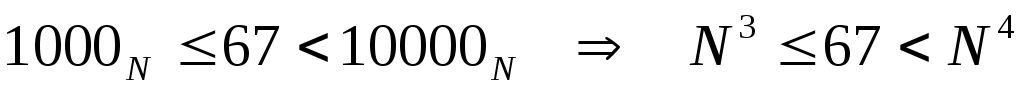
-
выпишем кубы и четвертые степени первых натуральных чисел, которые являются делителями числа 66:
-
видим, что из этого списка только для числа N = 3 выполняется условие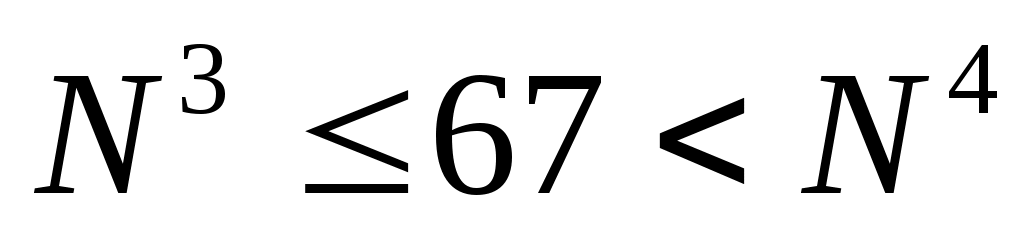
-
таким образом, верный ответ – 3. -
можно сделать проверку, переведя число 67 в троичную систему 6710 = 21113
Решение (программа на Python, А.Н. Носкин):
-
можно (но сложнее) решить задачу с помощью программы:
for i in range(2,37):# перебираем возможные основания
x = 67
x_N = ''
while x > 0:# перевод в N-ю систему
x_N += str(x%i)
x //= i
x_N = x_N[::-1]# разворот числа
if x_N[-1]== "1" and len(x_N) == 4:
print(i)
break
-
ответ: 3.
Решение (программа на Python, Б.С. Михлин):
-
Если при переводе из 10-й в N-ю систему счисления очередную полученную цифру дописывать слева к найденным ранее цифрам (т.е. так, как мы и делаем при ручном переводе), то не нужен будет разворот числа. -
Для i > 10 надо учитывать, что цифра может быть буквой. -
Верхняя граница основания 99 в цикле for i завышена. Арабских цифр и латинских букв хватит только для оснований до 10+26=36. Далее нет общепринятых правил обозначения цифр (если хотим получать N-ичное представление числа).
for N in range(2, 37): # подбираем основание от 2 до 36
x = 67
s = '' # в s будет представление числа в N-ичной системе
while x:
d = x % N # цифра (digit)
if d < 10:
d = str( d ) # цифра от 0 до 9
else:
d = chr( ord( 'A' ) + d - 10 ) # «цифра» от A до Z
s = d + s # цифру d приписываем слева к s
x //= N
if s[-1] == '1' and len( s ) == 4:
print( N )
break
-
возможен второй вариант: без представления всего числа в N-й системе счисления; здесь можно брать основание больше 36.
for N in range(2, 101): # подбираем основание от 2 до 100
x = 67
k = 0 # счетчик цифр (разрядов) N-ичного числа
while x:
d = x % N # очередная цифра (digit)
k += 1
if k == 1: d0 = d # d0 - младшая цифра
x //= N
if d0 == 1 and k == 4:
print( N )
break
-
ответ: 3.