Файл: Позиционные системы счисления.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 1047

Скачиваний: 9

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


  1. скопируем формулы из А2 и В1 вниз до того момента, когда частное станет равно 0 (это означает окончание процесса перевода):



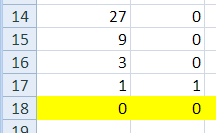
  1. подсчитаем в столбце В число остатков, равных 2:



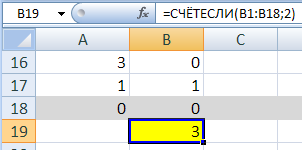
  1. Ответ: 3.

  2. в OpenOffice Calc нужно использовать такие формулы:

в A2: =QUOTIENT(A1;3)
в B1: =MOD(A1;3)

в B19: =COUNTIF(B1:B18;2)

Ещё пример задания:


Р-21. Сколько значащих нулей в двоичной записи числа
 4512 + 8512 – 2128 – 250

Решение (способ Е.А. Смирнова, Нижегородская область):

  1. Общая идея: количество значащих нулей равно количеству всех знаков в двоичной записи числа (его длине!) минус количество единиц

  2. приведём все числа к степеням двойки, учитывая, что 250 = 256 – 4 – 2 = 28 – 22 – 21:

4512 + 8512 – 2128 – 250 = (22)512 + (23)512 – 2128 – 28 + 22 + 21 =

= 21536 + 21024 – 2128 – 28 + 22 + 21

  1. старшая степень двойки – 21536, двоичная запись этого числа представляет собой единицу и 1536 нулей, то есть, состоит из 1537 знаков; таким образом, остаётся найти количество единиц

  2. вспомним, число 2N–2K при K < N записывается как N–K единиц и K нулей: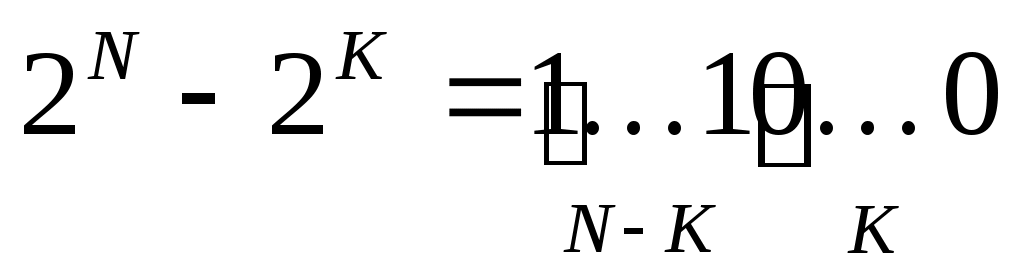

  3. для того чтобы использовать это свойство, нам нужно представить заданное выражение в виде пар вида 2N–2K, причём в этой цепочке степени двойки нужно выстроить по убыванию

  4. в нашем случае вы выражении

21536 + 21024 – 2128 – 28 + 22 + 21

стоит два знака «минус» подряд, это не позволяет сразу использовать формулу

  1. используем теперь равенство , так что – 2128 = – 2129 + 2128; получаем

21536
+ 21024 – 2129 + 2128 – 28 + 22 + 21

здесь две пары 2N–2K , а остальные слагаемые дают по одной единице

  1. общее число единиц равно 1 + (1024 – 129) + (128 – 8) + 1 + 1 = 1018

  2. таким образом, количество значащих нулей равно 1537 – 1018 = 519

  3. ответ: 519.

Решение (программа на Python, Б.С. Михлин):

  1. если доступна среда программирования на Python, можно написать программу, которая использует встроенную арифметику длинных чисел:

x = 4**512 + 8**512 - 2**128 - 250

print( bin(x)[2:].count('0') )

  1. ответ: 519.

Ещё пример задания:


Р-20. Сколько единиц в двоичной записи числа
 42015 + 8405 – 2150 – 122

Решение (способ Е.А. Смирнова, Нижегородская область):

  1. приведём все числа к степеням двойки, учитывая, что 122 = 128 – 4 – 2 = 27 – 22 – 21:

42015 + 8405 – 2150 – 122 = (22)2015 + (23)405 – 2150 – 27 + 22 + 21 =

= 24030 + 21215 – 2150 – 27 + 22 + 21

  1. вспомним, число 2N–2K при K < N записывается как N–K единиц и K нулей:

  2. для того чтобы использовать это свойство, нам нужно представить заданное выражение в виде пар вида 2N–2K, причём в этой цепочке степени двойки нужно выстроить по убыванию

  3. в нашем случае вы выражении

24030 + 21215 – 2150 – 27 + 22 + 21

стоит два знака «минус» подряд, это не позволяет сразу использовать формулу

  1. используем теперь равенство , так что – 2150 = – 2151 + 2150; получаем

24030 + 21215 – 2151 + 2150 – 27 + 22 + 21

здесь две пары 2N–2K , а остальные слагаемые дают по одной единице

  1. общее число единиц равно 1 + (1215 – 151) + (150 – 7) + 1 + 1 = 1210

  2. ответ: 1210.

Решение (С.О. Куров, Москва):

  1. приведём все числа к степеням двойки, учитывая, что 122 = 128 – 4 – 2 = 27 – 22 – 21:

42015 + 8405 – 2150 – 122 = (22)2015 + (23)405 – 2150 – 27 + 22 + 21 =

= 24030 + 21215 – 2150 – 27 + 22 + 21

  1. ищем в разности крайнюю левую степень двойки и крайнюю правую 21215 – 27, при этом 2150 на время «теряем»

  2. определяем количество единиц в разности 21215 – 27, получаем 1215 – 7 = 1208 единиц

  3. так как «внутри» этой разности есть еще 2150, то просто вычитаем одну единицу: 1208 – 1 = 1207; итого в разности 21215 – 2150 – 27 ровно 1207 единиц

  4. осталось прибавить по одной единицы от чисел 24030, 22, 21

  5. Ответ: 1210

Решение (программа на Python, Б.С. Михлин):

  1. используется встроенная «длинная арифметика» в Python:

x = bin( 4**2015 + 8**405 - 2**150 - 122 )

print( x.count( '1' ) )

  1. ответ: 1210.

Ещё пример задания:


Р-19. Решите уравнение .

Ответ запишите в троичной системе счисления. Основание системы счисления указывать не нужно.

Решение:

  1. переведём все числа в десятичную систему счисления:



  1. собирая всё в одно уравнение получаем



  1. это уравнение имеет два решения, 6 и -8; основание системы счисления – натуральное число, поэтому ответ – 6

  2. переводим ответ в троичную систему: 6 = 2∙31 = 203.

  3. ответ: 20.

Решение (программа на Python, А.Н. Носкин):

  1. можно (но сложнее) решить задачу перебором с помощью программы:

a = 1*7**2 + 0 + 1 # перевод "101" в 10-ю систему

c = a - 1 # число "121" в 10-й системе

for i in range(3,100):# перебираем возможные основания

b = 1*i**2 + 2*i + 1 # перевод в 10-ю систему числа "121"

if b == c:

x = i # основание системы счисления (в 10й системе)

break

x3 = ''

while x > 0:# перевод основания в 3-ю систему

x3 += str(x%3)

x //= 3

x3 = x3[::-1]# разворот числа

print(x3)

  1. ответ: 20.

Решение (программа на Python, Б.С. Михлин):

  1. вариант программы:

for x in range( 3, 37): # среди оснований от 3 до 36

if int( '121', x ) + 1 == int( '101', 7 ):

break

print('в 10 c.c:', x)

s = ''

while x:

s = str( x%3 ) + s

x //= 3

print( 'Ответ в 3 с.с:', s )

  1. ответ: 20.

Ещё пример задания:


Р-18. Сколько единиц в двоичной записи числа
 42014 + 22015 – 8

Решение:

  1. приведём все числа к степеням двойки:

42014 + 22015 – 8 = (22)2014 + 22015 – 23 = 24028 + 22015 – 23

  1. вспомним, что число 2N-1 в двоичной системе записывается как N единиц: ,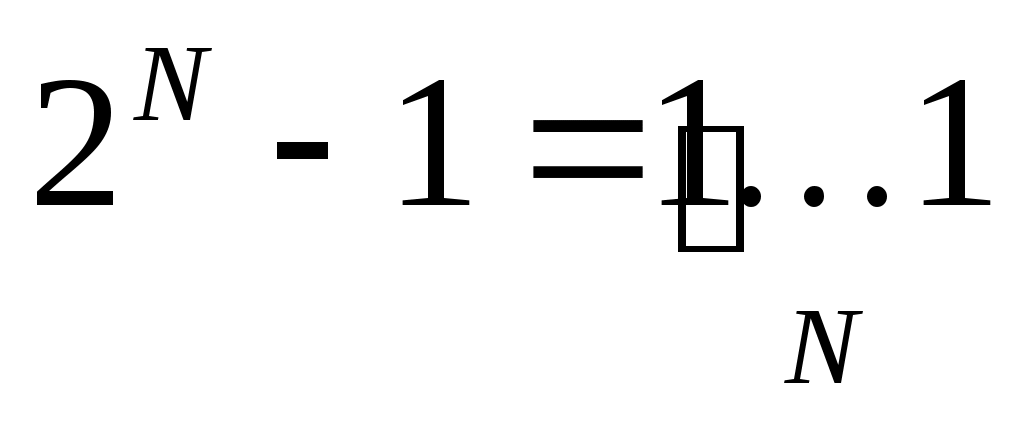
    а число 2N–2K при K < N записывается как N–K единиц и K нулей:

  2. согласно п. 2, число 22015 – 23 запишется как 2012 единиц и 3 нуля

  3. прибавление 24028 даст ещё одну единицу, всего получается 2012 + 1 = 2013 единиц

  4. ответ: 2013.

Решение (программа на Python, Б.С. Михлин):

  1. программа использует встроенную «длинную арифметику» Python:

x = bin( 4**2014 + 2**2015 - 8 )
print( x.count( '1' ) )

  1. ответ: 2013.

Ещё пример задания:


Р-17. Сколько единиц в двоичной записи числа
 42016 + 22018 – 8600 + 6

Решение:

  1. приведём все числа к степеням двойки, разложив 6 как 22+21

42016 + 22018 – 8600 + 6 = (22)2016 + 22018 - (23)600 + 22 + 21 = 24032 + 22018 – 21800 + 22 + 21

  1. вспомним, что число 2N-1 в двоичной системе записывается как N единиц: ,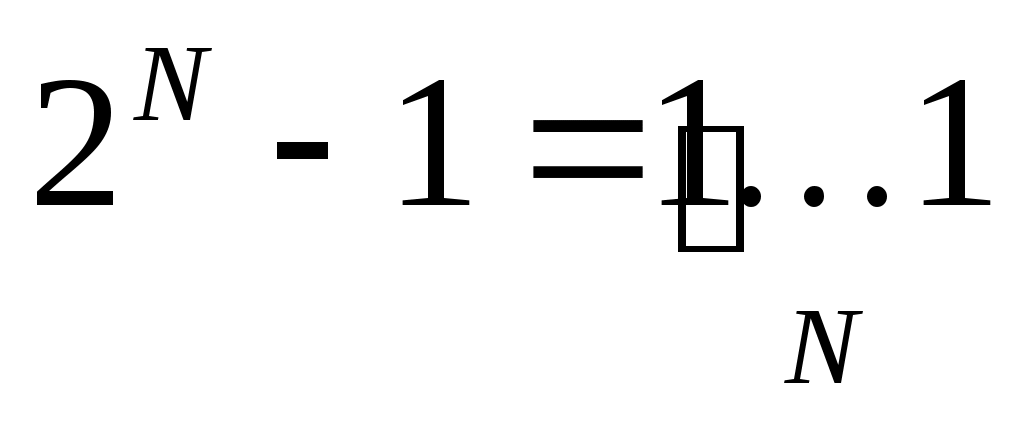
    а число 2N–2K при K < N записывается как N–K единиц и K нулей:

  2. согласно п. 2, число 22018 – 21800 запишется как 218 единиц и 1800 нулей

  3. прибавление 24032 даст ещё одну единицу, а прибавление 22 + 21 – ещё две, всего получается 218 + 3 = 221 единица

  4. ответ: 221.

Ещё пример задания:


Р-16. Сколько единиц в двоичной записи числа
 42016 – 22018 + 8800 – 80

Решение:

  1. приведём все числа к степеням двойки, разложив 80 как 26+24

42016 – 22018 + 8800 – 80 = (22)2016 – 22018

Смотрите также файлы