Файл: Лабораторная работа 1 движение с постоянным ускорением бригада 5.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 1281

Скачиваний: 29

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Уфимский государственный нефтяной технический университет»ЛАБОРАТОРНАЯ РАБОТА № 1.1

ДВИЖЕНИЕ С ПОСТОЯННЫМ УСКОРЕНИЕМ

Бригада 5Выполнил: ст. гр. БГГ–19–01 26.04.20 Р.Р. Миргалиев Проверил: д. физико-матем. н. И.К. ГималтдиновУфа – 2020Лабораторная работа №1.1.«Движение с равномерным ускорением».Цель работы:* Знакомство с применением физической модели МАТЕРИАЛЬНАЯ ТОЧКА (МТ).* Исследование движения МТ с постоянным ускорением.* Экспериментальное определение ускорения свободного падения на поверхности Земли.Краткая теория:МАТЕРИАЛЬНАЯ ТОЧКА – это абстрактный объект (модель), не имеющий размеров, но обладающий другими характеристиками реального тела.ПОЛОЖЕНИЕ МТ – это координата, которую имеет МТ в данный момент времени. Математическое описание положения МТ – ее радиус-вектор 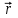.МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ есть изменение положения тела в пространстве со временем. Закон движения – это функция 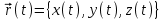.СКОРОСТЬ есть векторная кинематическая характеристика движения, показывающая быстроту и направление движения. Математически 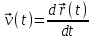.УСКОРЕНИЕ есть векторная кинематическая характеристика движения, показывающая быстроту и направление изменения скорости. Математически 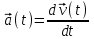. ТРАЕКТОРИЯ есть геометрическое место точек, которые проходит МТ при ее движении. В каждой точке вектор скорости направлен по касательной к траектории.Для движения с постоянным ускорением закон движения 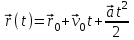, где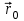

– начальное положение и 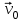– начальная скорость МТ. Закон скорости: .

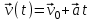При свободном движении тела вблизи поверхности Земли 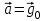- ускорению свободного падения.

ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ показывает, как быстро меняется величина скорости 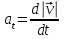; оно направлено по касательной к траектории.

НОРМАЛЬНОЕ УСКОРЕНИЕ показывает, как быстро меняется направление вектора скорости 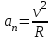(R – радиус кривизны траектории). Оно перпендикулярно касательной.

Полное ускорение определяется по теореме Пифагора: .

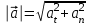Ход работы:

Начальная высота h=10 м

Начальный угол =45⁰


Номер измерения

Траект. 1 υ0 = 15 м/с
Траект. 2 υ0 = 17 м/с
Траект. 3

υ0 = 19 м/с
Траект. 4

υ0 = 22 м/с
Траект. 5

υ0 = 25 м/с




ymax
ymax
ymax
ymax
ymax
ymax
ymax
ymax
ymax
ymax

1
15,7
0
17,4
0
19,2
0
22,3
0
25,9
0

2
15,7
0
17,4
0
19,2
0
22,3
0
25,9
0

3
15,7
0
17,4
0
19,2
0
22,3
0
25,9
0

4
15,7
0
17,4
0
19,2
0
22,3
0
25,9
0

5
15,7
0
17,4
0
19,2
0
22,3
0
25,9
0

<ymax>
15,7
17,4
19,2
22,3
25,9

Абс. ош.
0
0
0
0
0
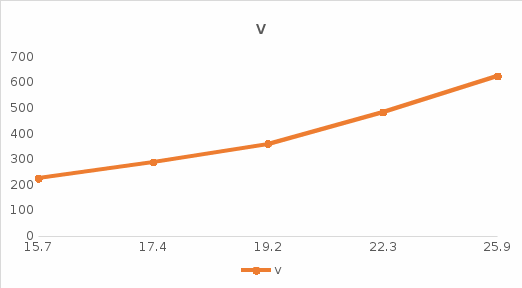
График зависимости средних значений вертикальной координаты точки максимального подъема от квадрата начальной скорости:Выведем формулу для ymax максимальной высоты подъема тела:Из формулы x=x0+V0t+(at2)/2 по аналогии получаем:ymax=y0+V0t+(gt2)/2.Т. к. 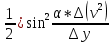в начальный момент времени V0=0, то формула приобретает вид:ymax=y0+(gt2)/2.Преобразуем формулу: gt2/2=y-y0gt2=2(y-y0)Отсюда получаем: t=Подставляем данное выражение в исходную формулу:y=y0+ Вычисление значения ускорения свободного падения g:g=g1= 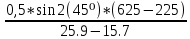= 9,8 м/с2 g2= 9,9 м/с2g3= 9.8 м/с2g4= 9.8 м/с2g5= 9.8 м/с2gср= (9,8+9,9+9.8+9,8+9,8)/5= 9,82 м/с2Δ (gср)= 0.Полученный экспериментально график зависимости значений вертикальной координаты точки максимального подъемаот квадрата начальной скорости имеет вид непрерывной ломаной кривойи качественно совпадает с теоретической зависимостью данных характеристик, имеющей вид y=y0+  .Вывод: Таким образом, мы исследовали движение материальной точки с постоянным ускорением и экспериментально определили ускорение свободного падения на поверхности Земли. Полученные значения полностью совпадают с исходными данными.Ответы на вопросы.

  1. Дайте определение материальной точки.
МАТЕРИАЛЬНАЯ ТОЧКА – это абстрактный объект (модель), не имеющий размеров, но обладающий другими характеристиками реального тела.

  1. Как определяется положение материальной точки?
Положение материальной точки – это координата, которую имеет МТ в данный момент времени. Математическое описание положения МТ – ее радиус-вектор
.

  1. Дайте определение системы отсчета.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени, по отношению к которым рассматривается движение материальных точек или тел.

  1. Что такое декартова система координат?
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве.

  1. Дайте определение механического движения.
Механическое движение - есть изменение положения тела в пространстве со временем. Закон движения – это функция .Министерство образования и науки Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Уфимский государственный нефтяной технический университет»ЛАБОРАТОРНАЯ РАБОТА № 1.4УПРУГИЕ И НЕУПРУГИЕ УДАРЫ Бригада 5Выполнил: ст. гр. БГГ–19–01 26.04.20 Р.Р. МиргалиевПроверил: д. физико-матем. н. И.К. ГималтдиновУфа – 2020Лабораторная работа №1.4.

«УПРУГИЕ И НЕУПРУГИЕ УДАРЫ».

ЦЕЛЬ РАБОТЫ:

  1. Выбор физических моделей для анализа взаимодействия двух тел.

  2. Исследование физических характеристик, сохраняющихся при столкновениях.

  3. Экспериментальное определение зависимости тепловыделения при неупругом столкновении от соотношения масс при разных скоростях.
КРАТКАЯ ТЕОРИЯ:СТОЛКНОВЕНИЕ (удар, соударение) – модель взаимодействия двух тел, длительность которого равна нулю (мгновенное событие). Применяется для описания реальных взаимодействий, длительностью которых можно пренебречь в условиях данной задачи.АБСОЛЮТНО УПРУГИЙ УДАР – столкновение двух тел, после которого форма и размеры сталкивающихся тел восстанавливаются полностью до состояния, предшествовавшего столкновению. Суммарные импульс и кинетическая энергия системы из двух таких тел сохраняются (после

столкновения такие же, какими были до столкновения):

; .

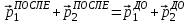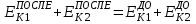АБСОЛЮТНО НЕУПРУГИЙ УДАР – столкновение двух тел, после которого форма и размеры тел не восстанавливаются, тела «слипаются» и движутся как одно целое с одной скоростью. Суммарный импульс двух неупруго сталкивающихся тел сохраняется, а кинетическая энергия становится меньше, так как часть энергии переходит в конечном итоге в тепловую:

, .

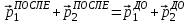Используя определение импульса и определение абсолютно неупругого удара, преобразуем закон сохранения импульса, спроектировав его на ось ОХ, вдоль которой движутся тела, в следующее уравнение:

(m1 + m2) ,

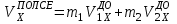а закон для кинетической энергии преобразуем в такое уравнение:

ЕТЕПЛ = 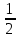[m1(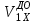 )2+ m2( 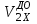)2 – (m1 + m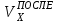2) ( )2].

Помножив и разделив второе уравнение на (m1 + m2) и используя первое уравнение, получим:

ЕТЕПЛ = 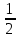[m1(m1 + m2)( 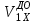)2 + m2(m1 + m2)( 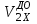)2 – (m1 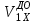+ m2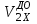 )2]/(m1 + m2)

Относительная величина тепловой энергии  равна отношению

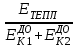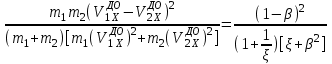= = , где

Смотрите также файлы