ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 111
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
и 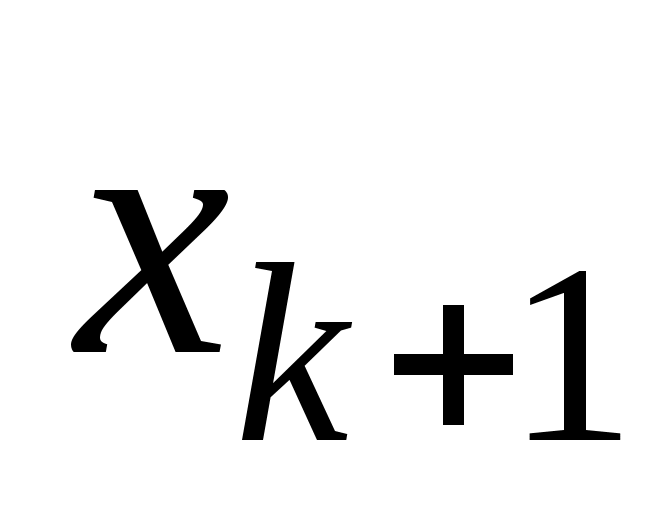 . Очевидно, что маршрут можно задать последовательностью его вершин
. Очевидно, что маршрут можно задать последовательностью его вершин 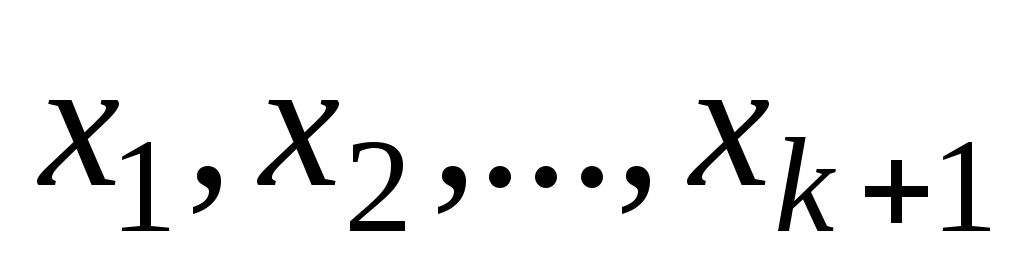 или последовательностью ребер
или последовательностью ребер 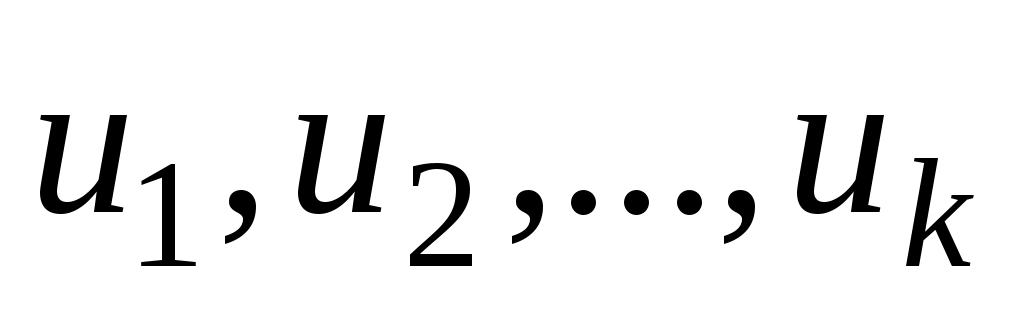 . Маршрут называется цепью, если все его ребра различны, и простой цепью, если все его вершины, кроме, возможно, крайних, различны. Гамильтоновой цепью называется простая цепь, содержащая все вершины графа.
. Маршрут называется цепью, если все его ребра различны, и простой цепью, если все его вершины, кроме, возможно, крайних, различны. Гамильтоновой цепью называется простая цепь, содержащая все вершины графа.
Маршрут называется циклическим, если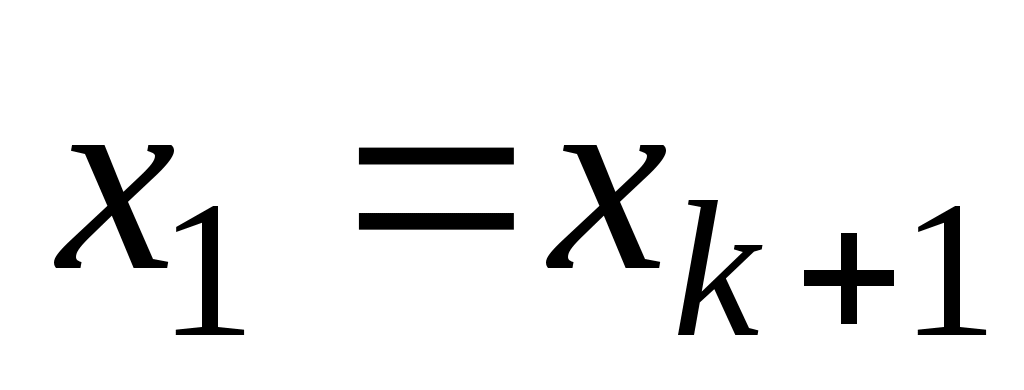 . Циклическая цепь называется циклом, а циклическая простая цепь — простым циклом. Число ребер в маршруте — длина маршрута. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа. Длина всякого цикла не менее трех в графе без петель и кратных ребер. Минимальная из длин циклов графа называется его обхватом.
. Циклическая цепь называется циклом, а циклическая простая цепь — простым циклом. Число ребер в маршруте — длина маршрута. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа. Длина всякого цикла не менее трех в графе без петель и кратных ребер. Минимальная из длин циклов графа называется его обхватом.
Важным понятием теории графов является связность. Граф называется связным, если любые две его несовпадающие вершины соединены маршрутом.
Р
ис. 1.14. Граф
В подавляющем большинстве случаев граф задается матрицей. Для расчетов на ЭВМ это единственный способ. Наиболее часто граф задают с помощью матриц смежности и инциденций.
Рассмотрим изображенный на рис. 1.14 граф. Как для орграфов, так и для неориентированных графов можно определить матрицу смежности вершин. Это квадратная матрица
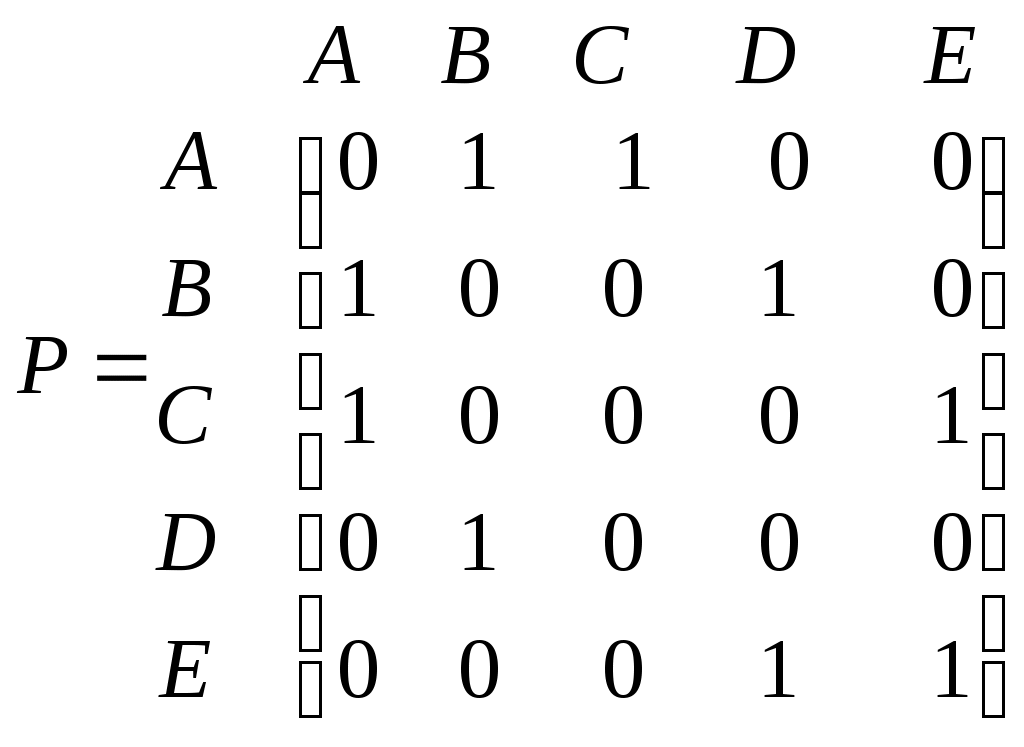
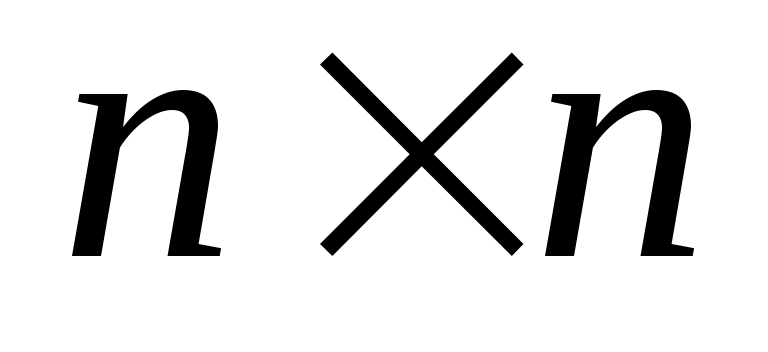 порядка, где
порядка, где  — число вершин. Ее строки и столбцы соответствуют вершинам графа. Элементы
— число вершин. Ее строки и столбцы соответствуют вершинам графа. Элементы  матрицы смежности вершин равны числу дуг, идущих из
матрицы смежности вершин равны числу дуг, идущих из  -той вершины в
-той вершины в 
-ю вершину. Если орграф не содержит параллельных дуг, то матрица является бинарной и состоит только из нулей и единиц. В случае неориентированного графа ему вместе с ребром принадлежит и ребро
принадлежит и ребро  , поэтому матрица смежности вершин будет симметрической. Матрица смежности вершин однозначно определяет структуру графа. Аналогично можно определить и матрицу смежности дуг.
, поэтому матрица смежности вершин будет симметрической. Матрица смежности вершин однозначно определяет структуру графа. Аналогично можно определить и матрицу смежности дуг.
Определим для рассматриваемого графа без ребра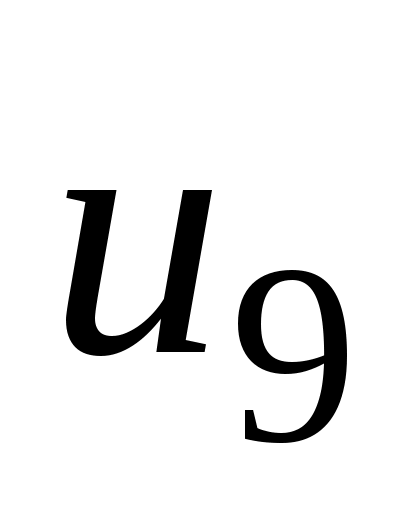 матрицу инциденций. Это прямоугольная матрица размерности
матрицу инциденций. Это прямоугольная матрица размерности  , где
, где  — число вершин, а
— число вершин, а 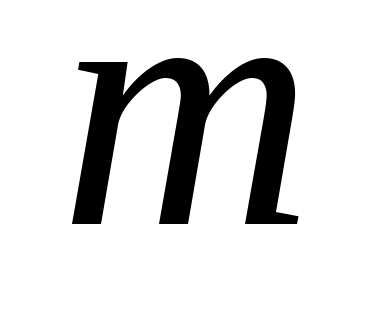 — число дуг. Элементы
— число дуг. Элементы 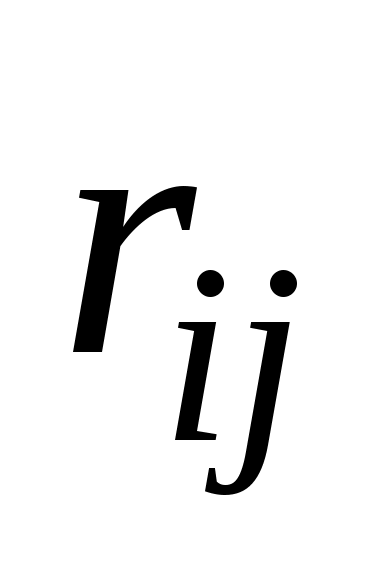 этой матрицы равны плюс единице, если дуга
этой матрицы равны плюс единице, если дуга  исходит из
исходит из  -й вершины (начальная вершина), минус единице, если дуга
-й вершины (начальная вершина), минус единице, если дуга  входит в
входит в 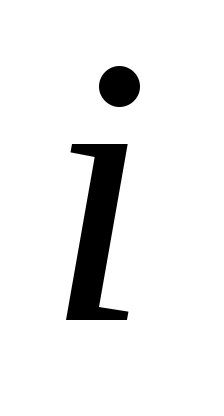 -ю вершину (конечная вершина), нулю, если дуга не инцидентна
-ю вершину (конечная вершина), нулю, если дуга не инцидентна 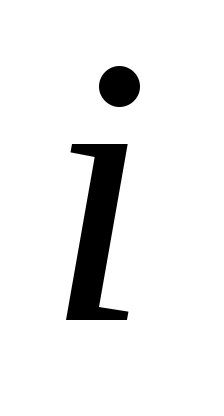 -й вершине. В случае неориентированного графа элементами матрицы будут числа единица и нуль, т. е.
-й вершине. В случае неориентированного графа элементами матрицы будут числа единица и нуль, т. е.
 .
.
Строки матрицы инциденций называют векторами инциденций графа . Матрица инциденций
. Матрица инциденций
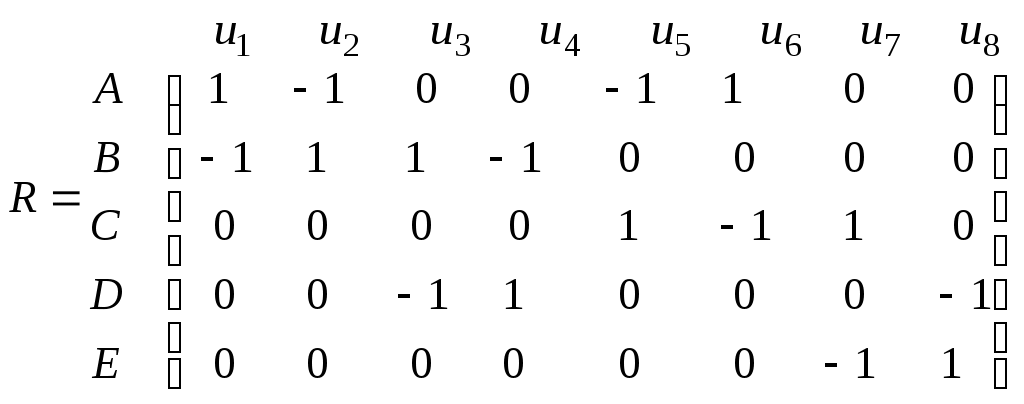
также однозначно определяет структуру графа.
Весьма важным видом графа является связный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны единственным путем.
Рассмотрим связный граф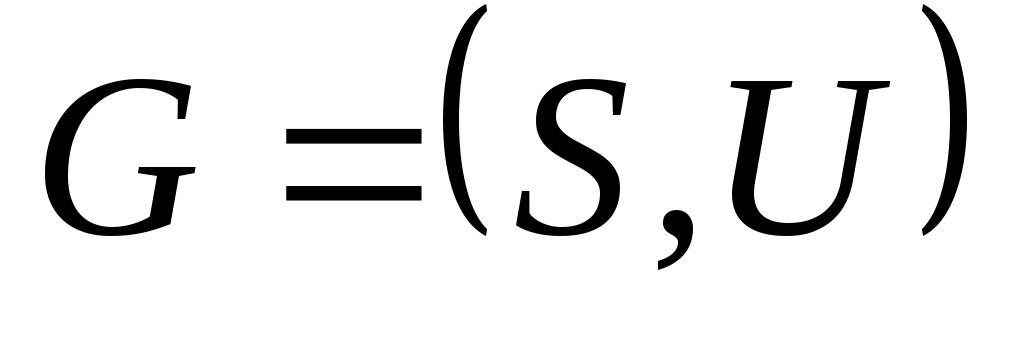
, пусть и
и  — две его вершины. Длина кратчайшего
— две его вершины. Длина кратчайшего 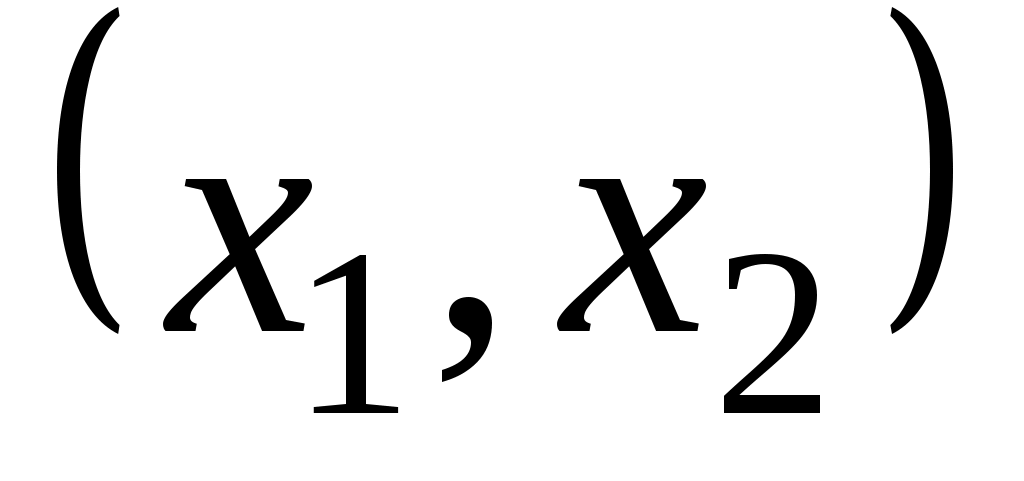 -маршрута называется расстоянием между вершинами
-маршрута называется расстоянием между вершинами  и
и  , обозначается через
, обозначается через 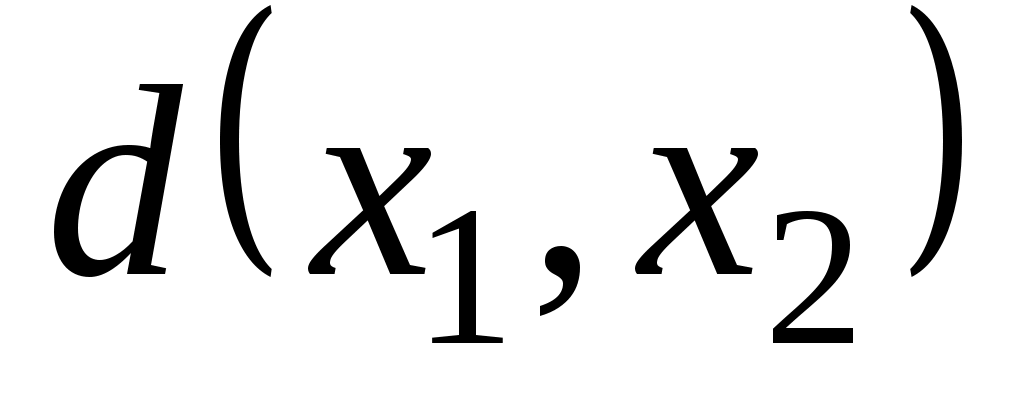 . Очевидно, что расстояние между вершинами является простой цепью и
. Очевидно, что расстояние между вершинами является простой цепью и 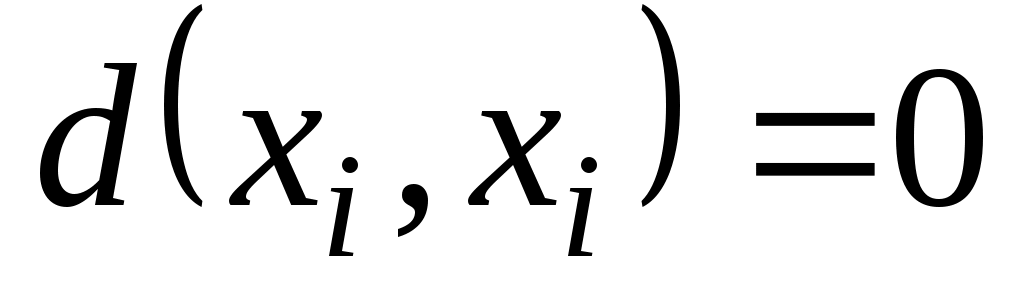 . Для любой вершины
. Для любой вершины  величина
величина
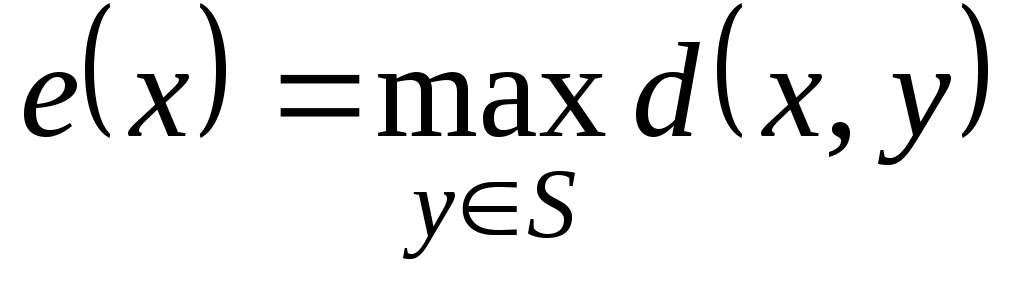 (1.13.6)
(1.13.6)
называется эксцентриситетом вершины . Максимальный из всех эксцентриситетов вершин называется диаметром графа и обозначается
. Максимальный из всех эксцентриситетов вершин называется диаметром графа и обозначается  , т. е.
, т. е.
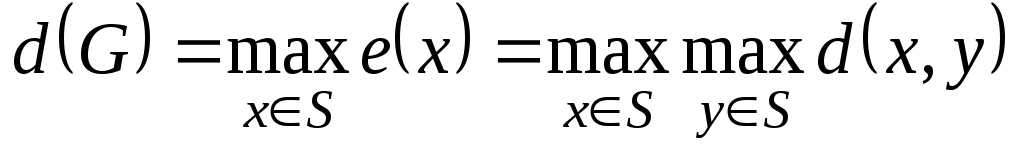 . (1.13.7)
. (1.13.7)
Минимальный из эксцентриситетов вершин графа называется его радиусом и обозначается через :
:
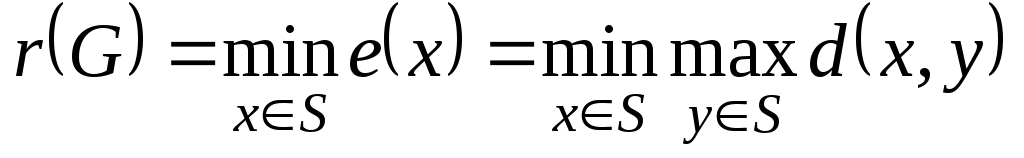 . (1.13.8)
. (1.13.8)
Вершина периферийная, если ее эксцентриситет равен диаметру графа, т. е.
периферийная, если ее эксцентриситет равен диаметру графа, т. е. 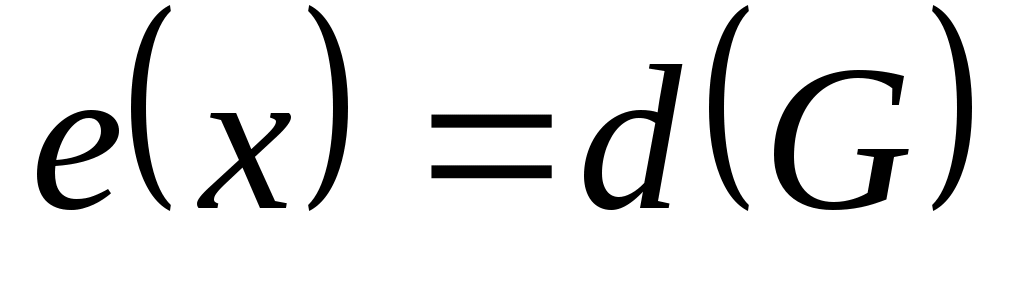 . Простая цепь, расстояние между концами которой равно
. Простая цепь, расстояние между концами которой равно  , называется диаметральной цепью.
, называется диаметральной цепью.
Рис. 1.15. Центр графа
В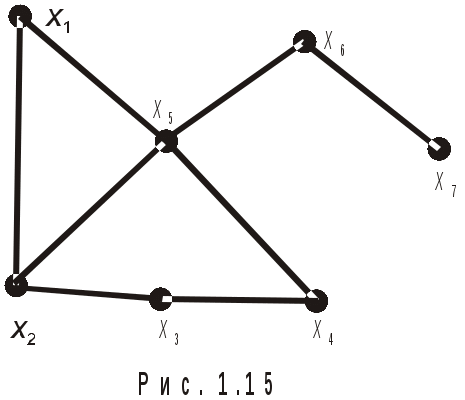
ершина центральная, если
центральная, если 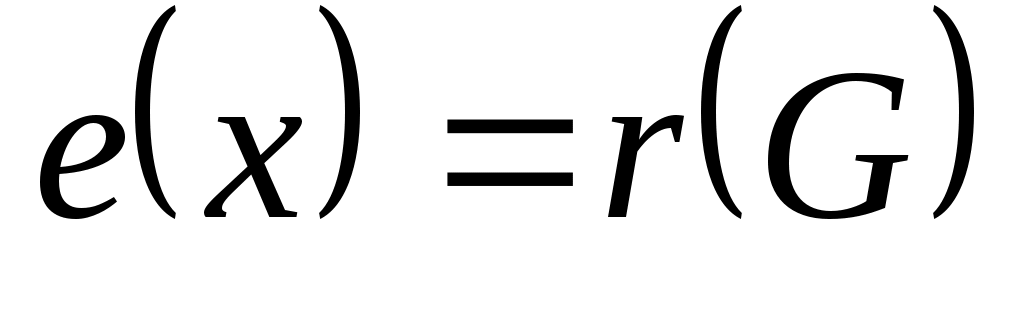 . Множество всех центральных вершин графа называется его
. Множество всех центральных вершин графа называется его
центром. Центром может быть единственная вершина графа или несколько вершин. На рис. 1.15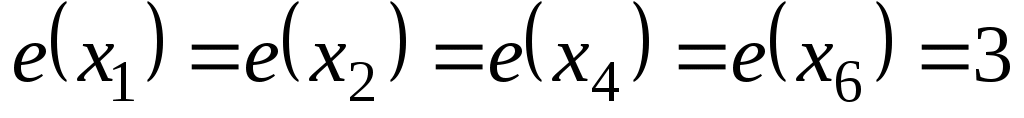 ,
, 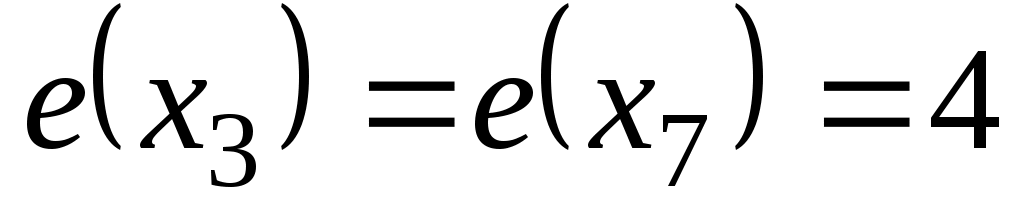 ,
, 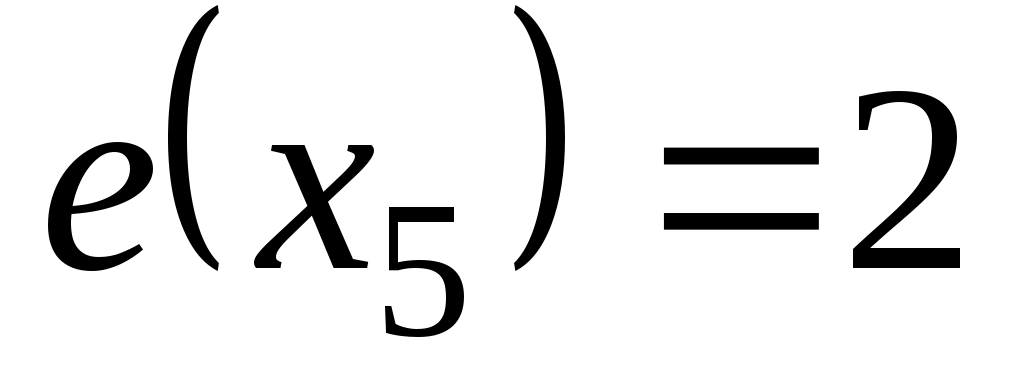 . Таким образом,
. Таким образом, 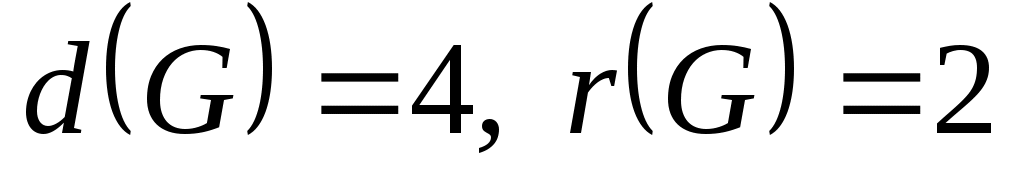 . Периферийные вершины
. Периферийные вершины 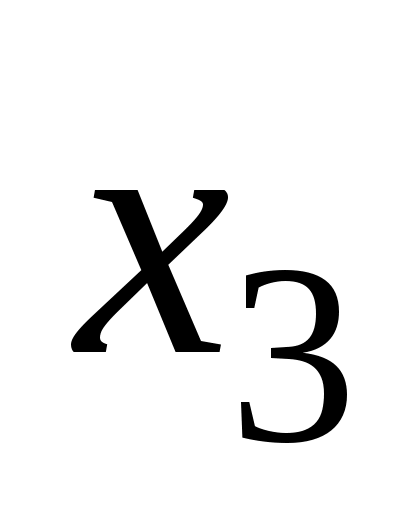 и
и 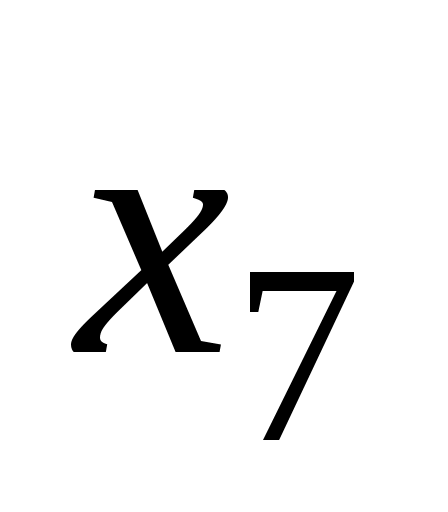 , диаметральные цепи
, диаметральные цепи 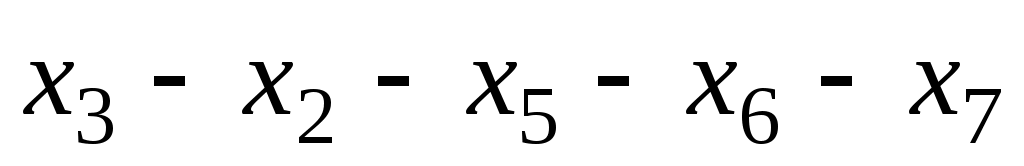 и
и 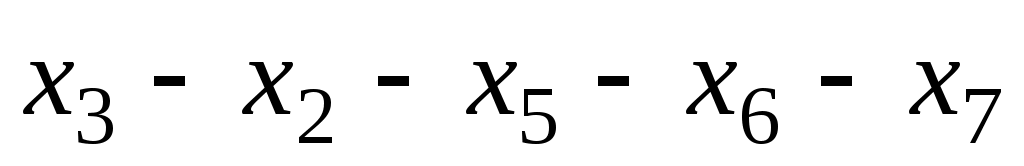 , центральная вершина
, центральная вершина 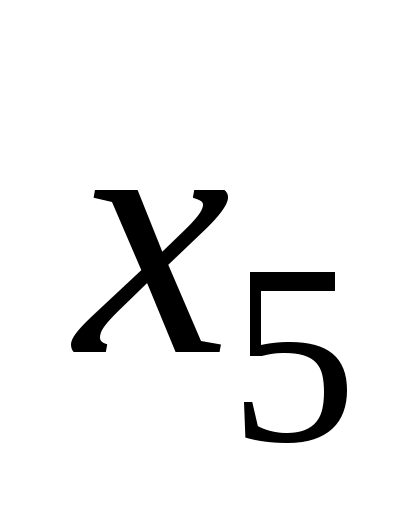 .
.
1 Клод Элвуд Шеннон (1916—2001 гг.) — американский математик.
2 Ральф Хартли (1881—1970 гг.) — американский инженер и изобретатель.
3 Джино Фано (1871—1952 гг.) — итальянский математик.
4 Огастес Морган (де Морган) (1806—1875 гг.) — шотландский математик и логик.
5 Леонард Эйлер (1707—1783 гг.) — швейцарский математик.
6 Джон Венн (1834—1923 гг.) — английский математик и логик.
Маршрут называется циклическим, если
Важным понятием теории графов является связность. Граф называется связным, если любые две его несовпадающие вершины соединены маршрутом.
Р

ис. 1.14. Граф
В подавляющем большинстве случаев граф задается матрицей. Для расчетов на ЭВМ это единственный способ. Наиболее часто граф задают с помощью матриц смежности и инциденций.
Рассмотрим изображенный на рис. 1.14 граф. Как для орграфов, так и для неориентированных графов можно определить матрицу смежности вершин. Это квадратная матрица
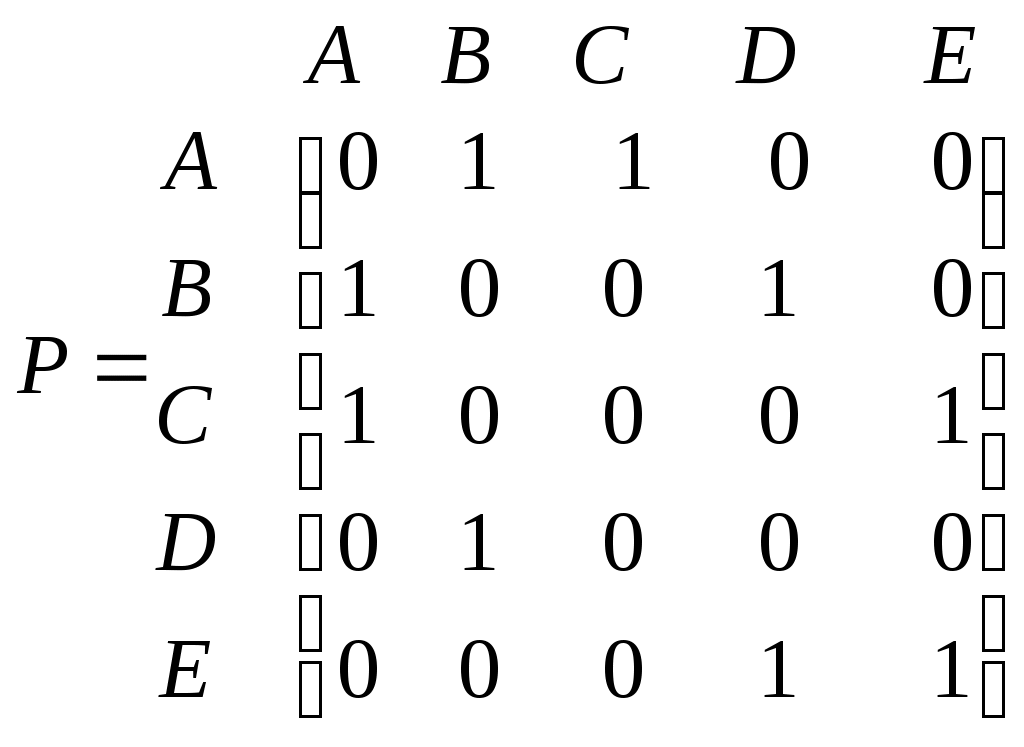
-ю вершину. Если орграф не содержит параллельных дуг, то матрица является бинарной и состоит только из нулей и единиц. В случае неориентированного графа ему вместе с ребром
Определим для рассматриваемого графа без ребра
 .
.Строки матрицы инциденций называют векторами инциденций графа
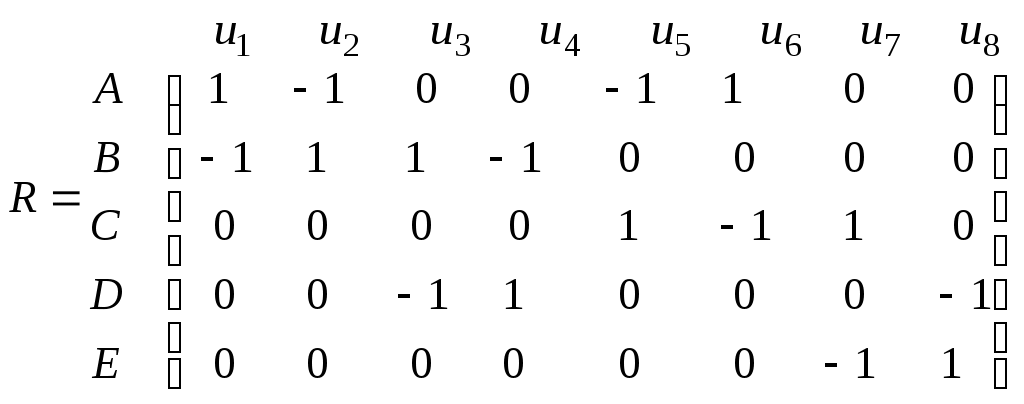
также однозначно определяет структуру графа.
Весьма важным видом графа является связный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны единственным путем.
Рассмотрим связный граф
, пусть
называется эксцентриситетом вершины
Минимальный из эксцентриситетов вершин графа называется его радиусом и обозначается через
Вершина
Рис. 1.15. Центр графа
В

ершина
центром. Центром может быть единственная вершина графа или несколько вершин. На рис. 1.15
1 Клод Элвуд Шеннон (1916—2001 гг.) — американский математик.
2 Ральф Хартли (1881—1970 гг.) — американский инженер и изобретатель.
3 Джино Фано (1871—1952 гг.) — итальянский математик.
4 Огастес Морган (де Морган) (1806—1875 гг.) — шотландский математик и логик.
5 Леонард Эйлер (1707—1783 гг.) — швейцарский математик.
6 Джон Венн (1834—1923 гг.) — английский математик и логик.