ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 117
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
называется строгим порядком и определяется таким образом:  и
и  . Это отношение не является частичным порядком, так как не удовлетворяет условию рефлексивности
. Это отношение не является частичным порядком, так как не удовлетворяет условию рефлексивности 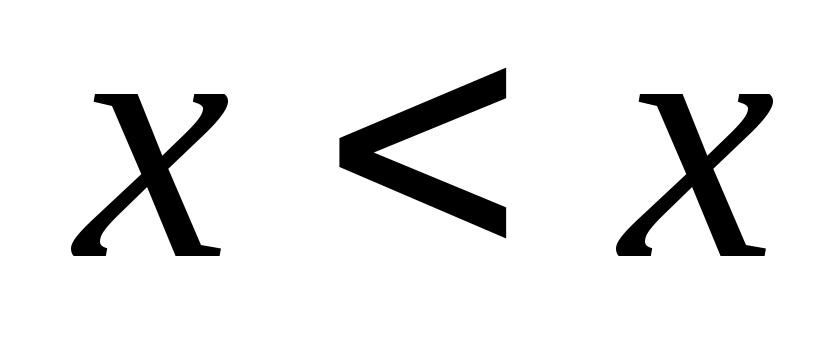 .
.
Если во множестве есть элементы
есть элементы  и
и  , о которых нельзя сказать, что
, о которых нельзя сказать, что  или
или 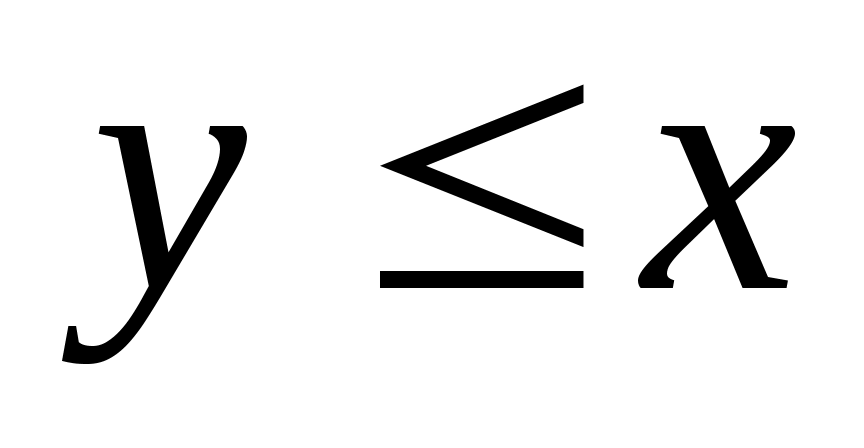 , то такие элементы называются несравнимыми. Частичный порядок называется линейным порядком, если любые два элемента
, то такие элементы называются несравнимыми. Частичный порядок называется линейным порядком, если любые два элемента  и
и  из множества
из множества  сравнимы, т. е.
сравнимы, т. е.  или
или 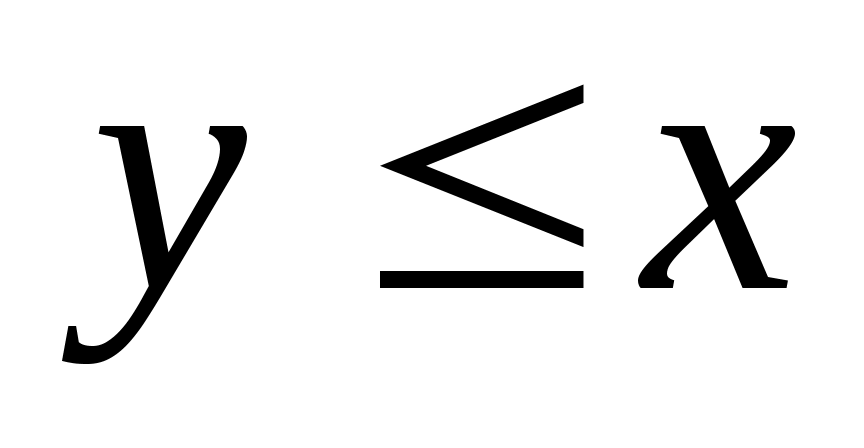 .
.
Непустое множество , на котором зафиксирован некоторый частичный (линейный) порядок, называется частично (линейно) упорядоченным множеством. Элемент
, на котором зафиксирован некоторый частичный (линейный) порядок, называется частично (линейно) упорядоченным множеством. Элемент  частично упорядоченного множества
частично упорядоченного множества  называется максимальным (минимальным), если для
называется максимальным (минимальным), если для 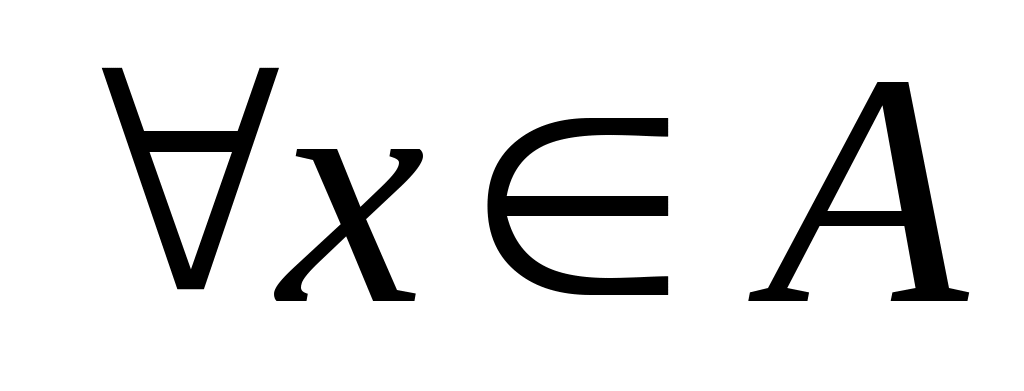 из того, что
из того, что 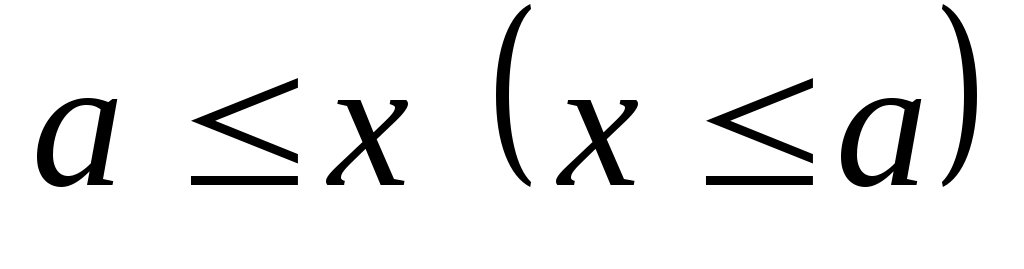 , следует
, следует 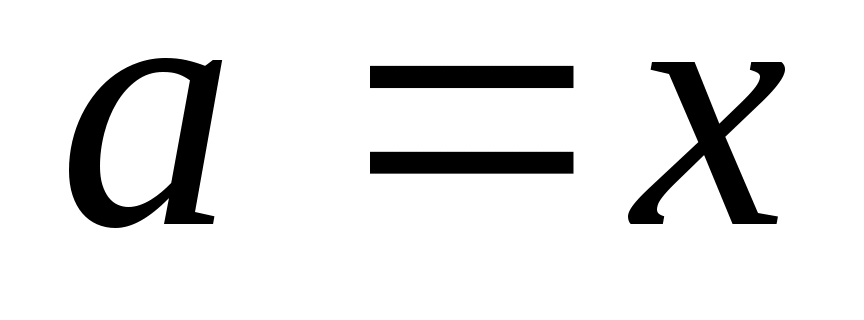 . Элемент
. Элемент  называется наибольшим (наименьшим), если
называется наибольшим (наименьшим), если 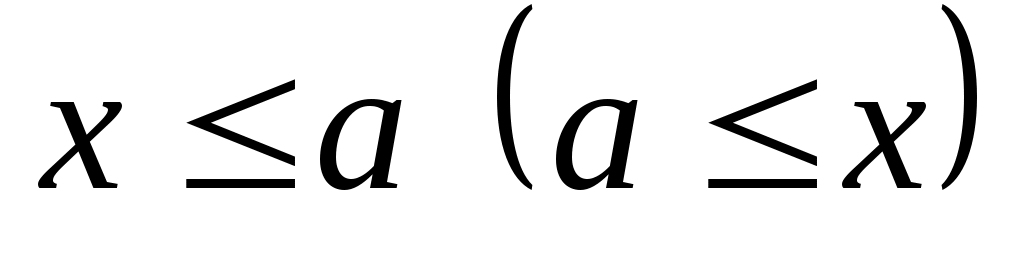
для всех . Наибольший элемент обозначается
. Наибольший элемент обозначается  , наименьший —
, наименьший — 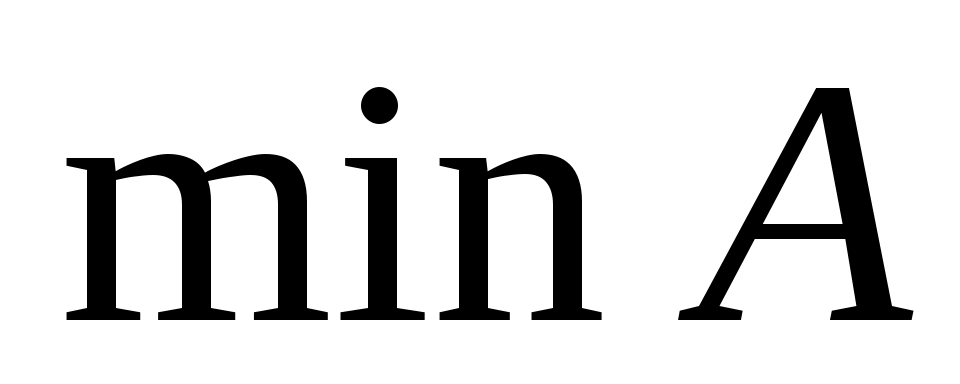 . Этих элементов у множества может и не быть, например, линейно упорядоченное множество рациональных чисел
. Этих элементов у множества может и не быть, например, линейно упорядоченное множество рациональных чисел 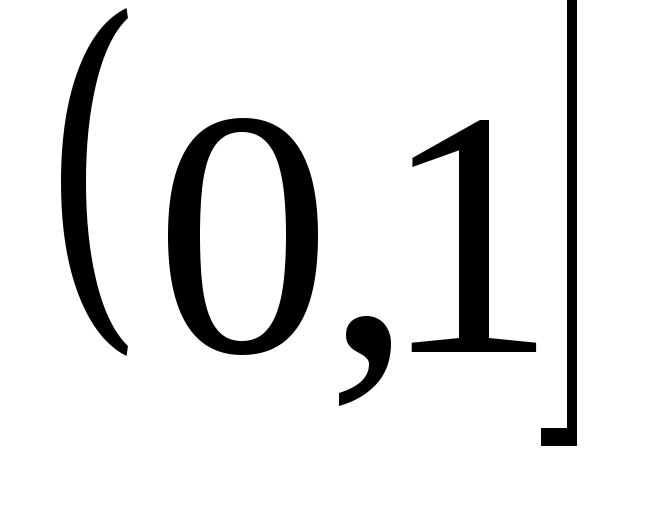 не имеет наименьшего элемента, наибольший элемент равен единице.
не имеет наименьшего элемента, наибольший элемент равен единице.
Верхней (нижней) гранью подмножества частично упорядоченного множества
частично упорядоченного множества  называется всякий элемент
называется всякий элемент  и такой, что
и такой, что 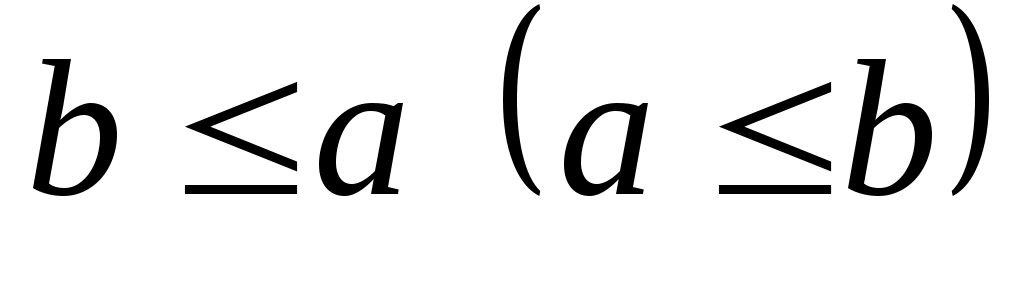 для всех
для всех 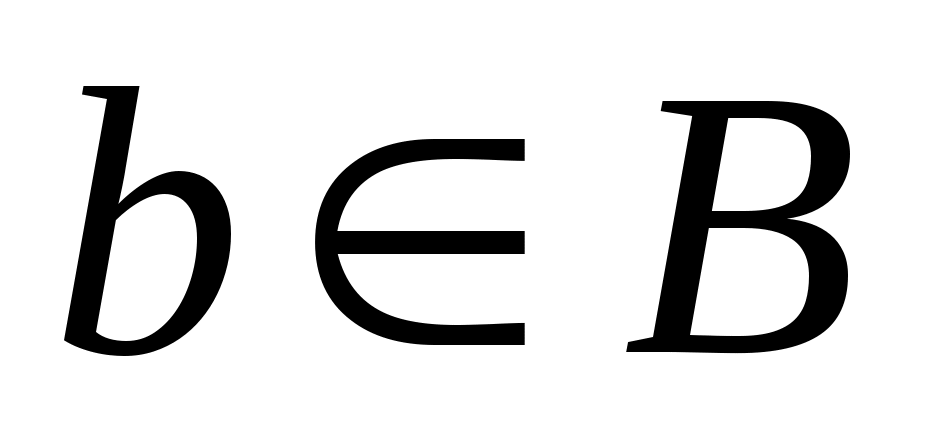 . Точной верхней (нижней) гранью подмножества
. Точной верхней (нижней) гранью подмножества 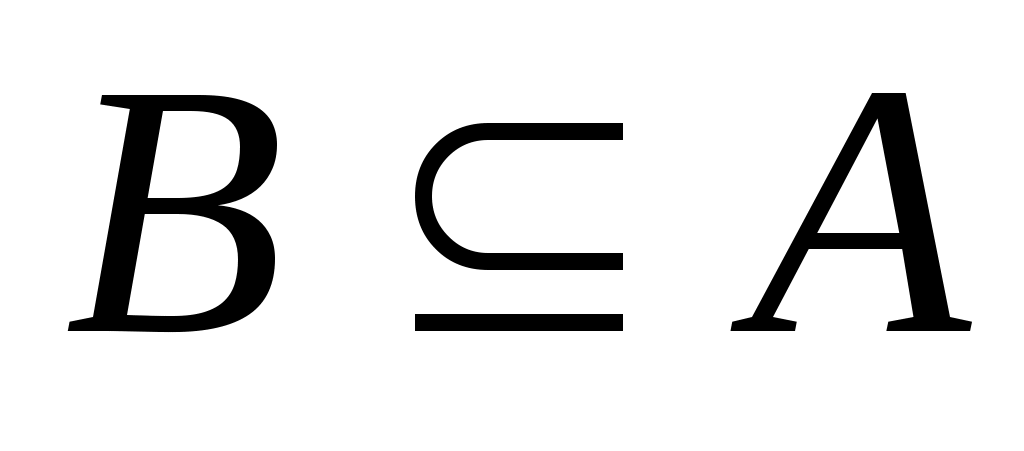 называется наименьшая верхняя (наибольшая нижняя) грань для
называется наименьшая верхняя (наибольшая нижняя) грань для  . Точная верхняя и точная нижняя грани множества
. Точная верхняя и точная нижняя грани множества 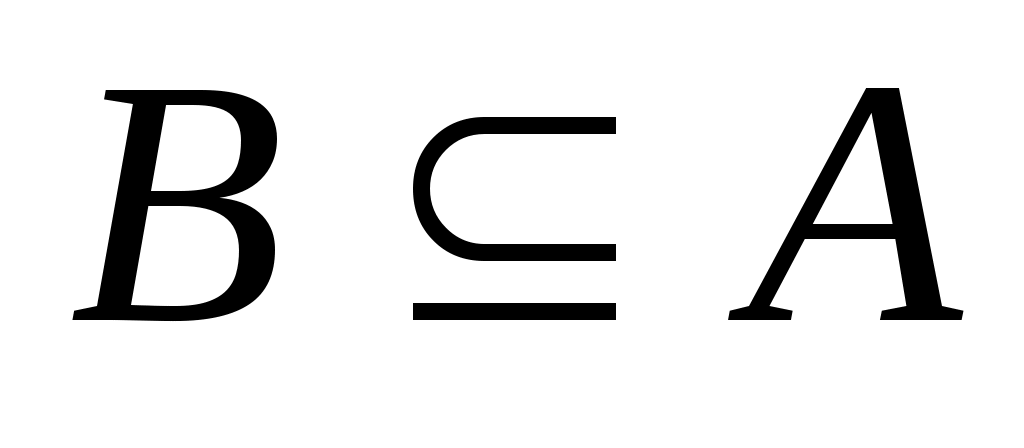 обозначаются через
обозначаются через 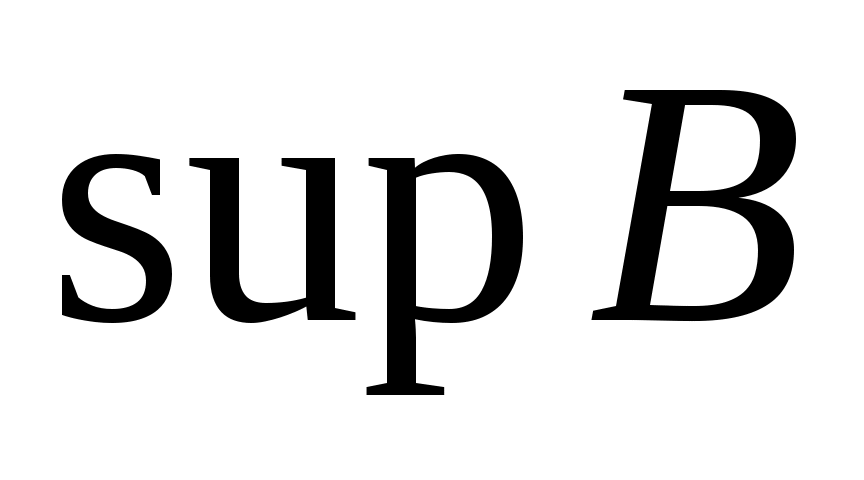 (супремум) и
(супремум) и 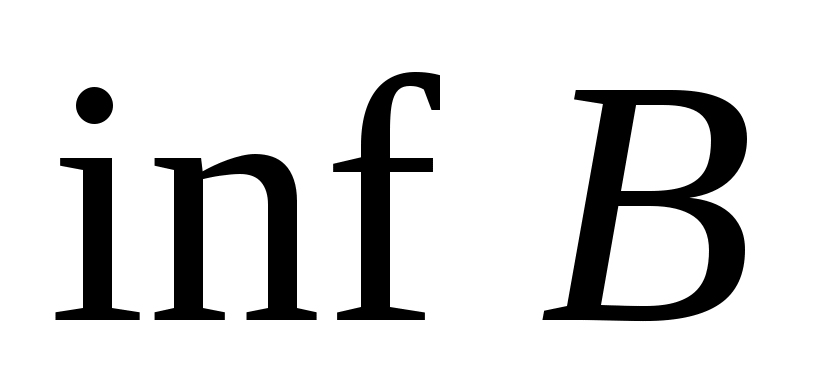 (инфимум) соответственно.
(инфимум) соответственно.
Линейный порядок на множестве
на множестве  называется полным, если каждое непустое подмножество множества
называется полным, если каждое непустое подмножество множества  имеет наименьший элемент. В этом случае множество
имеет наименьший элемент. В этом случае множество  называется вполне упорядоченным.
называется вполне упорядоченным.
Граф задается парой множеств. Пусть — непустое множество,
— непустое множество, 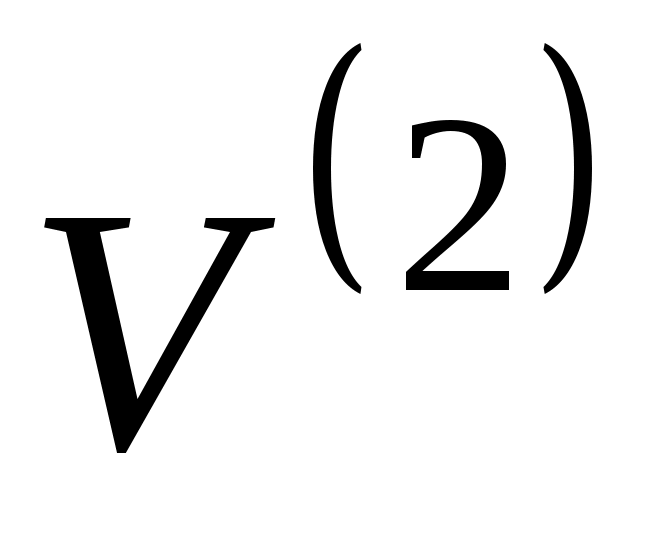 — множество всех его двухэлементных подмножеств,
— множество всех его двухэлементных подмножеств, 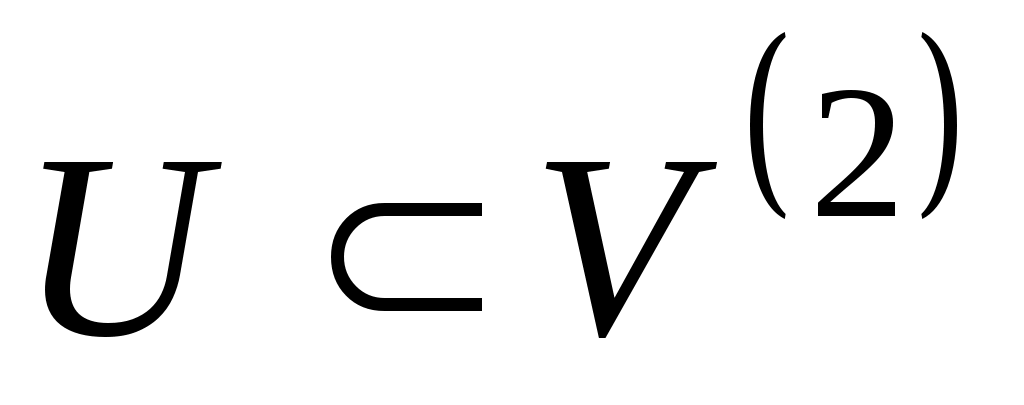 . Тогда пара
. Тогда пара  называется неориентированным графом. Элементы множества
называется неориентированным графом. Элементы множества  называются вершинами графа, а элементы множества
называются вершинами графа, а элементы множества 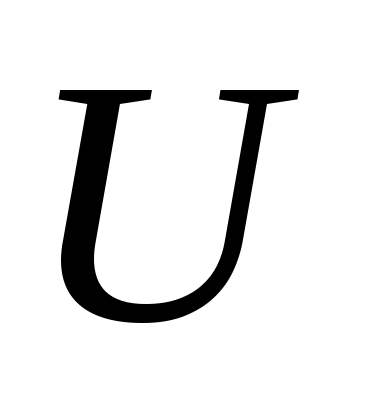 — ребрами. Итак,
— ребрами. Итак,  граф — это конечное множество вершин
граф — это конечное множество вершин  и множество ребер
и множество ребер 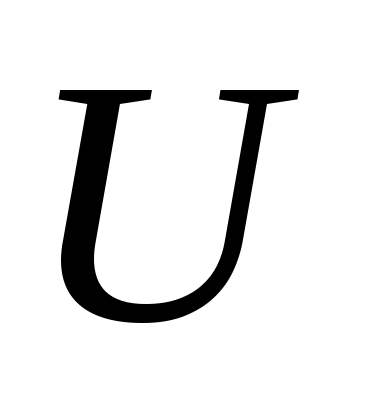 .
.
Вершины графа обозначают по-разному: или большими буквами, или малыми с индексами; для ребер наиболее употребительное обозначение с индексом, например,
с индексом, например,  . Взаимное расположение, форма и длина ребер значения не имеют. Важно лишь то, что они соединяют две данные вершины множества
. Взаимное расположение, форма и длина ребер значения не имеют. Важно лишь то, что они соединяют две данные вершины множества 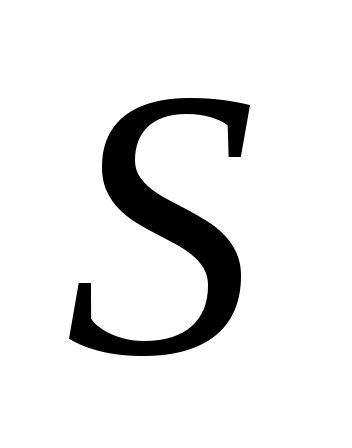 .
.
Если в паре вершин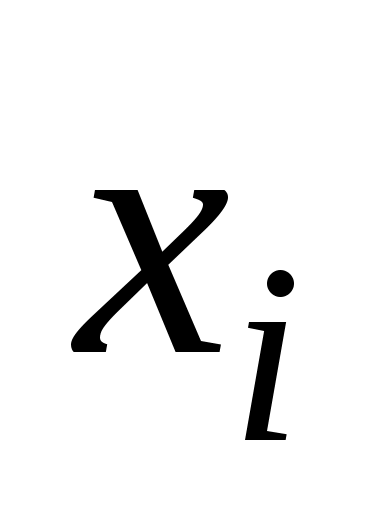 и
и  указано направление связи, т. е. какая из вершин является первой, то соединяющий их отрезок
указано направление связи, т. е. какая из вершин является первой, то соединяющий их отрезок 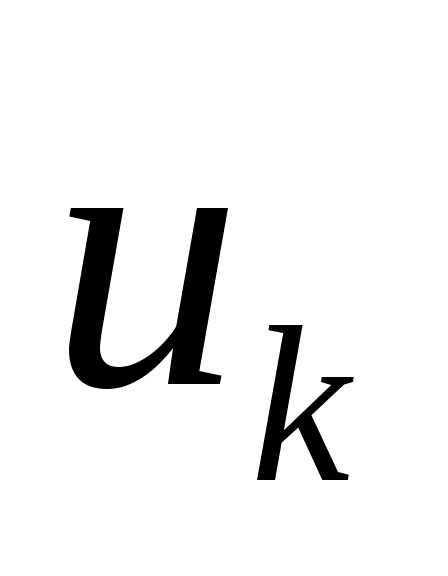 называется дугой, а вершины, определяющие дугу
называется дугой, а вершины, определяющие дугу 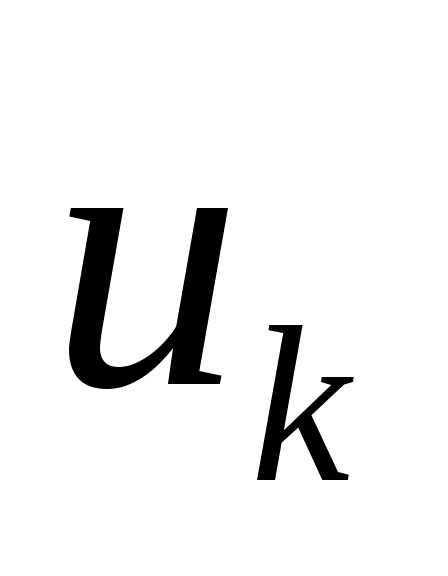
, называют концевыми вершинами. Если концевые вершины совпадают, то дугу называют петлей. В графе могут существовать дуги (ребра) с одинаковыми концевыми вершинами. Такие дуги называются параллельными.
могут существовать дуги (ребра) с одинаковыми концевыми вершинами. Такие дуги называются параллельными.
Если в графе все элементы множества
все элементы множества  изображаются дугами, то граф называется ориентированным или орграфом, если ребрами, то неориентированным. Два ребра называются смежными, если они имеют общий конец.
изображаются дугами, то граф называется ориентированным или орграфом, если ребрами, то неориентированным. Два ребра называются смежными, если они имеют общий конец.
Вершина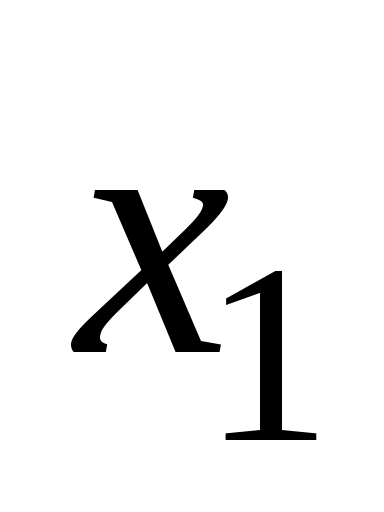 и ребро
и ребро 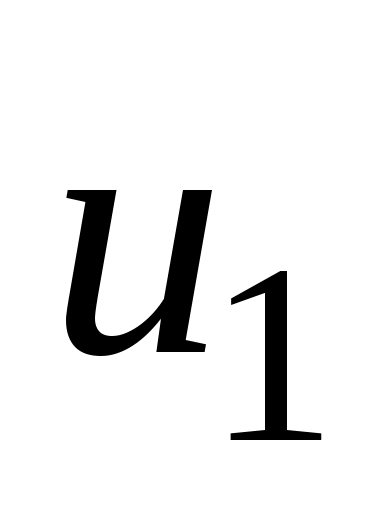 называются инцидентными, если
называются инцидентными, если 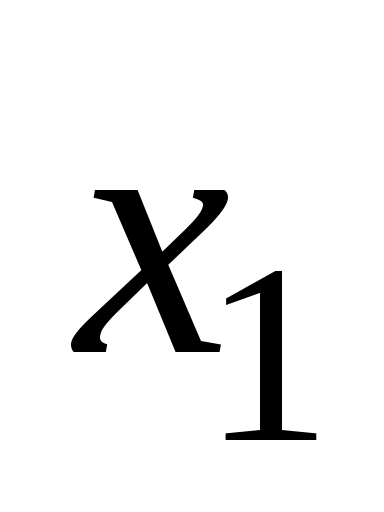 является концом ребра
является концом ребра 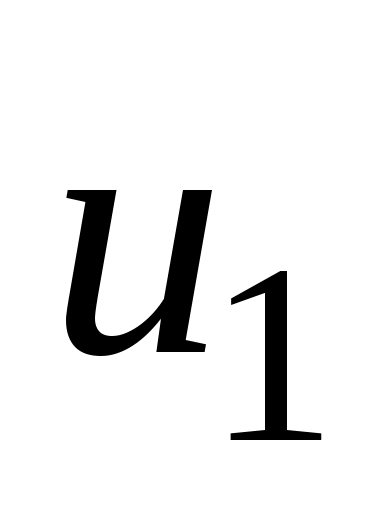 , и не инцидентными в противном случае. Таким образом, смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.
, и не инцидентными в противном случае. Таким образом, смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.
Число вершин графа называется его порядком. Степенью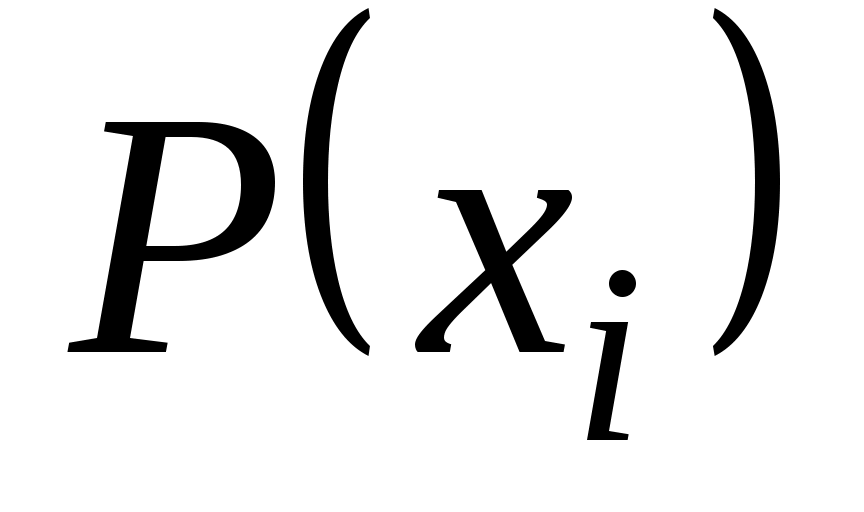 вершины
вершины 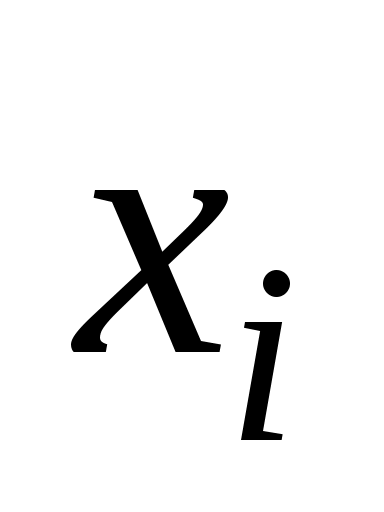 называется число дуг (ребер) графа
называется число дуг (ребер) графа  , инцидентных данной вершине. Вершина степени нуль называется изолированной, а если степень равна единице, то такая вершина называется висячей.
, инцидентных данной вершине. Вершина степени нуль называется изолированной, а если степень равна единице, то такая вершина называется висячей.
Граф простой, если он не содержит петель и параллельных дуг. Простой граф, в котором каждая пара вершин смежна, называется полным. Граф, содержащий хотя бы две параллельные дуги (ребра), — мультиграф. Граф, содержащий петли, — псевдограф.
простой, если он не содержит петель и параллельных дуг. Простой граф, в котором каждая пара вершин смежна, называется полным. Граф, содержащий хотя бы две параллельные дуги (ребра), — мультиграф. Граф, содержащий петли, — псевдограф.
Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. Два графа и
и 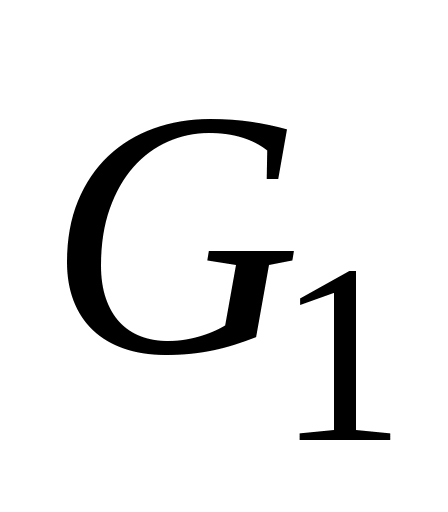 называются изоморфными
называются изоморфными
, если между множеством их вершин существует такое взаимно однозначное соответствие, при котором в одном из графов ребрами соединены вершины в том и только в том случае, если в другом графе ребрами соединены те же вершины. Для орграфов ориентация дуг должна быть также одинаковой.
Очевидно, что отношение изоморфизма графов является эквивалентностью, т. е. оно симметрично, транзитивно и рефлексивно. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны.
Способов задания графов — великое множество. Самый простой способ — задание множеств и
и  . Граф также может быть задан просто рисунком. В силу изоморфизма один и тот же граф может быть изображен разными рисунками.
. Граф также может быть задан просто рисунком. В силу изоморфизма один и тот же граф может быть изображен разными рисунками.
Р
ис. 1.13. Основной и дополнительный графы
Граф называется плоским (планарным), если он может быть изображен на плоскости так, что все пересечения ребер являются его вершинами. Для произвольного графа следующим образом определяется дополнительный граф (дополнение)
следующим образом определяется дополнительный граф (дополнение) 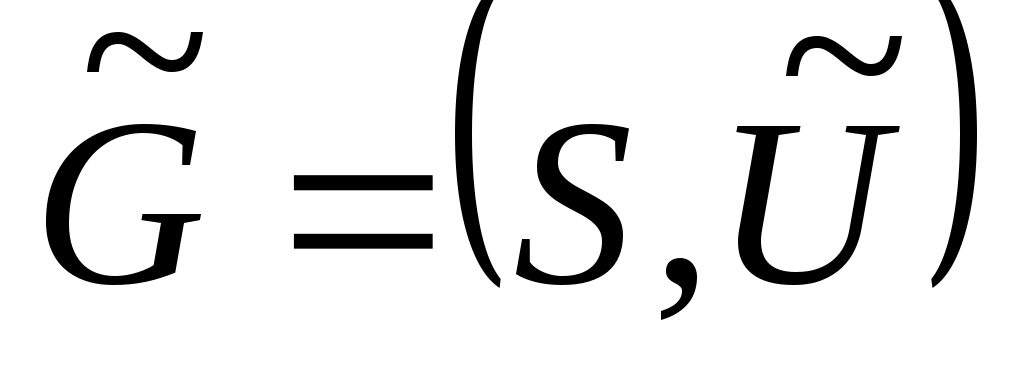 . В этом графе
. В этом графе 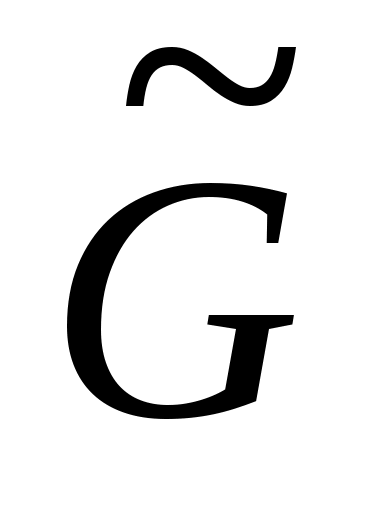 вершин столько же, сколько в графе
вершин столько же, сколько в графе  , причем любые две несовпадающие вершины смежны в
, причем любые две несовпадающие вершины смежны в 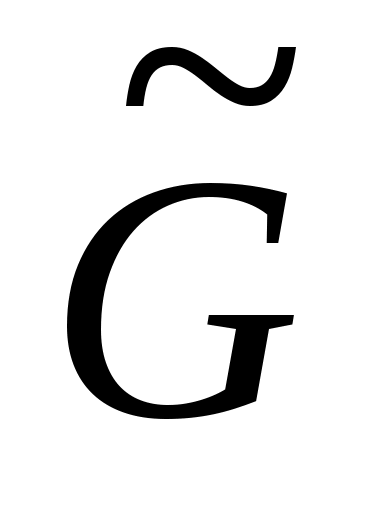 тогда и только тогда, когда они не смежны в
тогда и только тогда, когда они не смежны в  (рис. 1.13).
(рис. 1.13).
Чередующая последовательность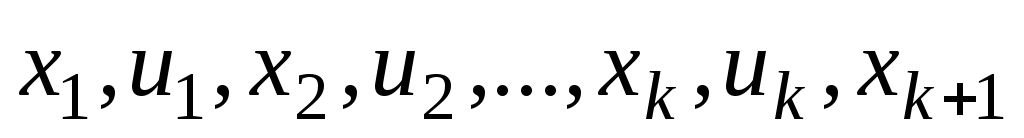 вершин и ребер графа, такая что
вершин и ребер графа, такая что 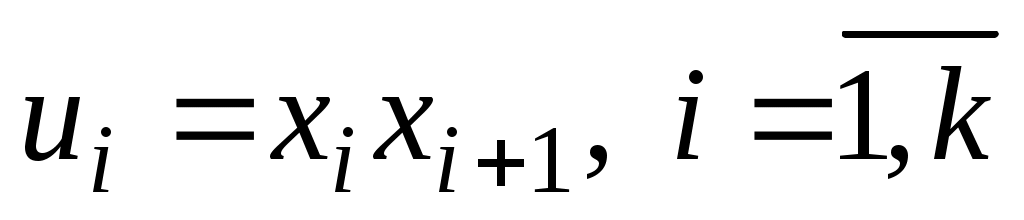 , называется маршрутом, соединяющим вершины
, называется маршрутом, соединяющим вершины 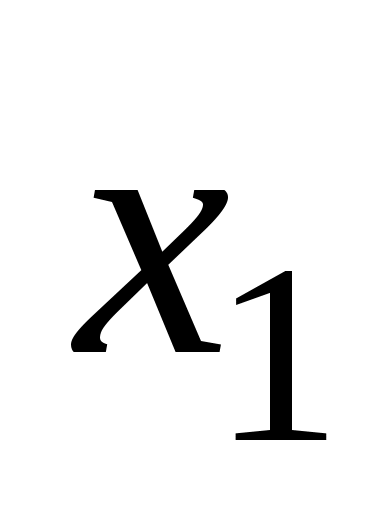
Если во множестве
Непустое множество
для всех
Верхней (нижней) гранью подмножества
Линейный порядок
1.13.3. Элементы теории графов
Граф задается парой множеств. Пусть
Вершины графа обозначают по-разному: или большими буквами, или малыми с индексами; для ребер наиболее употребительное обозначение
Если в паре вершин
, называют концевыми вершинами. Если концевые вершины совпадают, то дугу называют петлей. В графе
Если в графе
Вершина
Число вершин графа называется его порядком. Степенью
Граф
Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. Два графа
, если между множеством их вершин существует такое взаимно однозначное соответствие, при котором в одном из графов ребрами соединены вершины в том и только в том случае, если в другом графе ребрами соединены те же вершины. Для орграфов ориентация дуг должна быть также одинаковой.
Очевидно, что отношение изоморфизма графов является эквивалентностью, т. е. оно симметрично, транзитивно и рефлексивно. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны.
Способов задания графов — великое множество. Самый простой способ — задание множеств
Р

ис. 1.13. Основной и дополнительный графы
Граф называется плоским (планарным), если он может быть изображен на плоскости так, что все пересечения ребер являются его вершинами. Для произвольного графа
Чередующая последовательность