ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 114
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, пересечения и дополнения иногда называются законами алгебры множеств. Эти законы аналогичны правилам для равносильностей в булевой алгебре (1.13.1)—(1.13.3).
Часто элементы разных множеств связаны различными соотношениями, например, соотношениями порядка. -местным отношением или
-местным отношением или  -местным предикатом
-местным предикатом 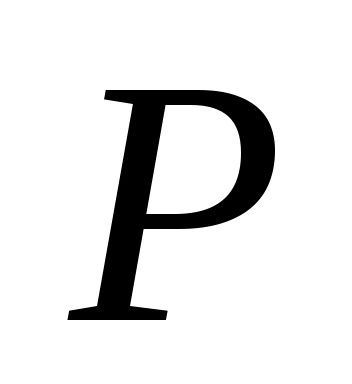 на множествах
на множествах  называется любое подмножество декартова произведения
называется любое подмножество декартова произведения 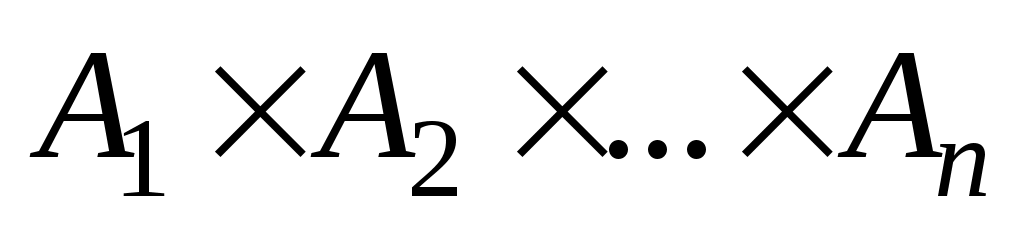 . Обозначение
. Обозначение  -местного отношения
-местного отношения 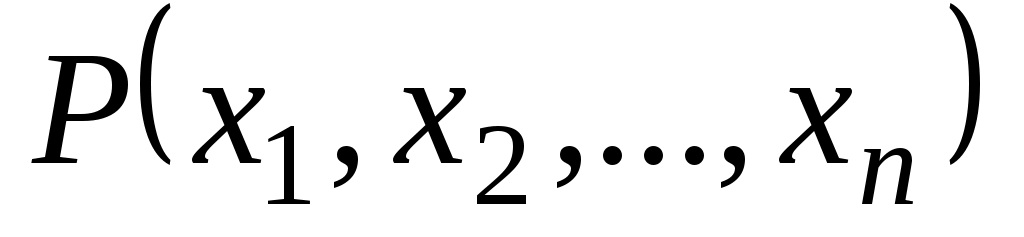 . При
. При  отношение
отношение 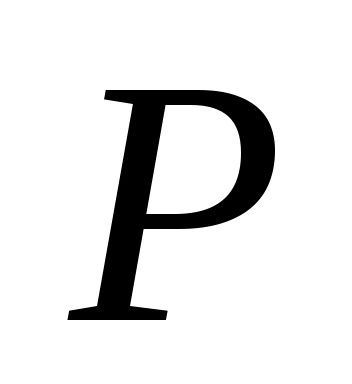 называется унарным и является подмножеством множества
называется унарным и является подмножеством множества  . Бинарным (или двуместным при
. Бинарным (или двуместным при 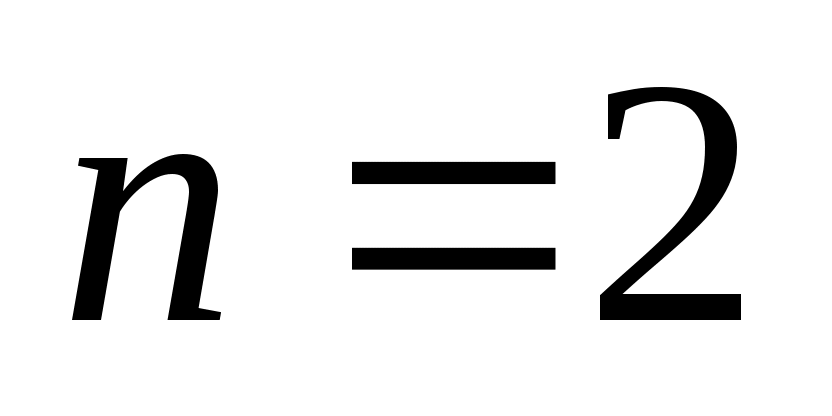 ) отношением называется множество упорядоченных пар. Элементы
) отношением называется множество упорядоченных пар. Элементы 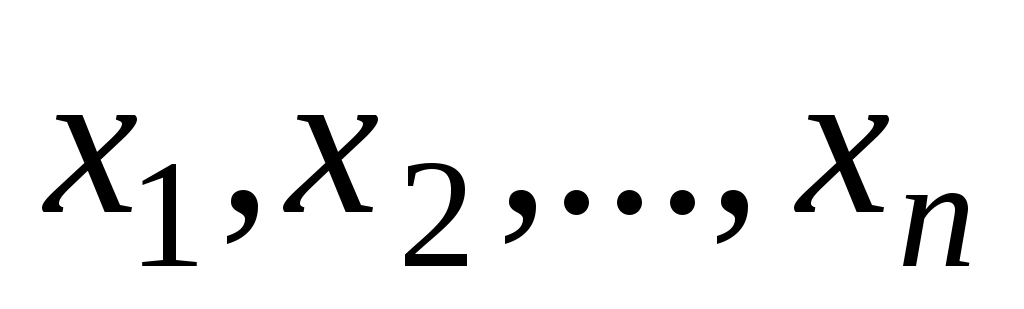 называются координатами или компонентами отношения
называются координатами или компонентами отношения 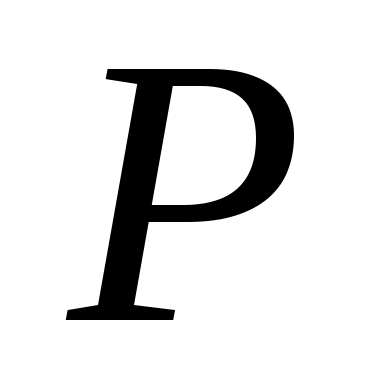 .
.
В теории множеств важную роль играют два вида специальных бинарных отношений: отношения эквивалентности и отношения порядка. Прообразами этих отношений служат интуитивные понятия равенства, предшествования и предпочтения.
Рассмотрим два конечных множества ,
, 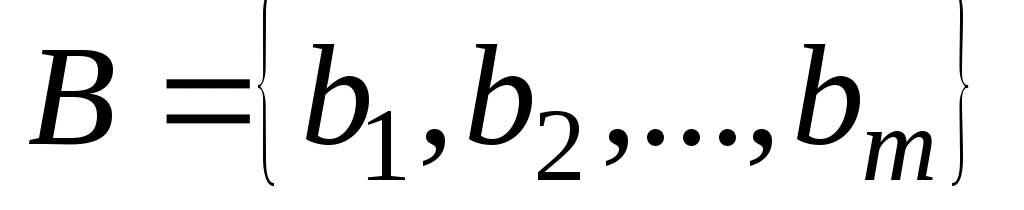 и бинарное отношение
и бинарное отношение 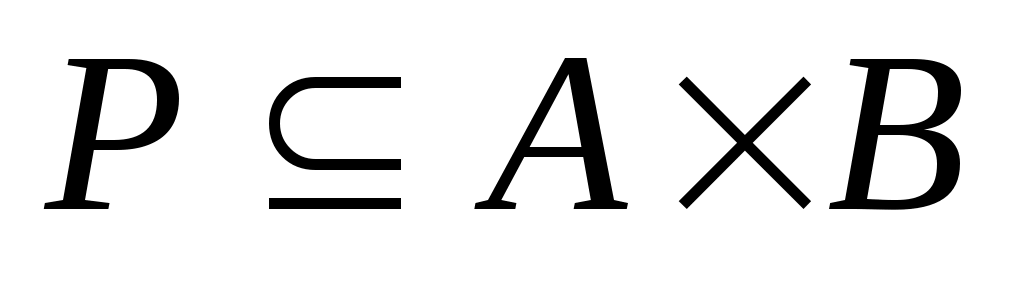 . Введем матрицу
. Введем матрицу  бинарного отношения
бинарного отношения 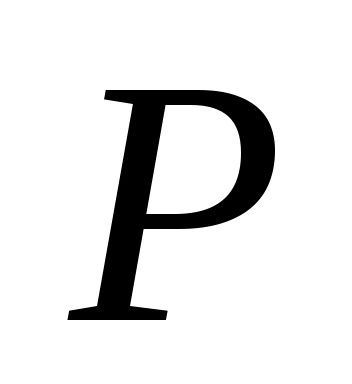
следующим образом:
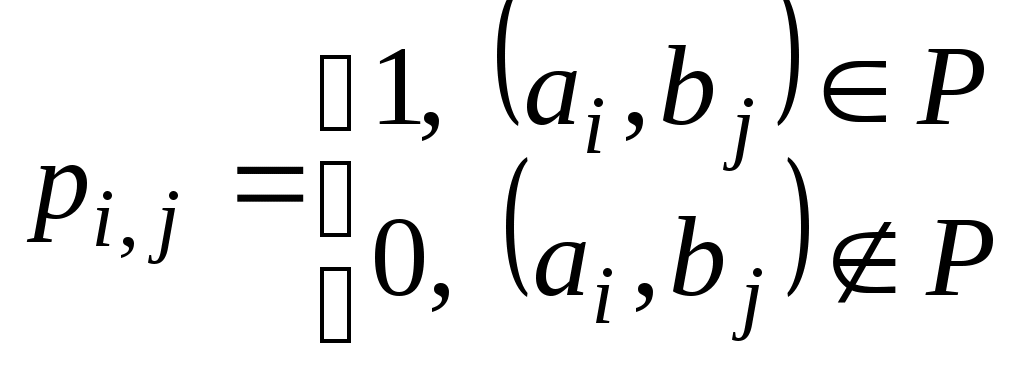 .
.
Эта матрица содержит полную информацию о связях между элементами множеств и
и  и позволяет представить эту информацию в графическом виде.
и позволяет представить эту информацию в графическом виде.
Матрица любого бинарного отношения обладает следующими свойствами:
Пример 1. Бинарное отношение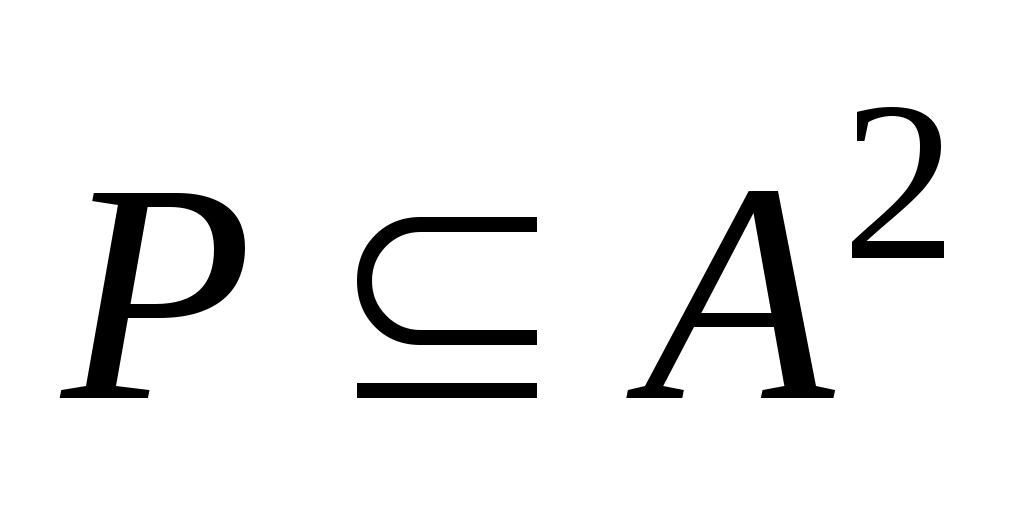 ,
, 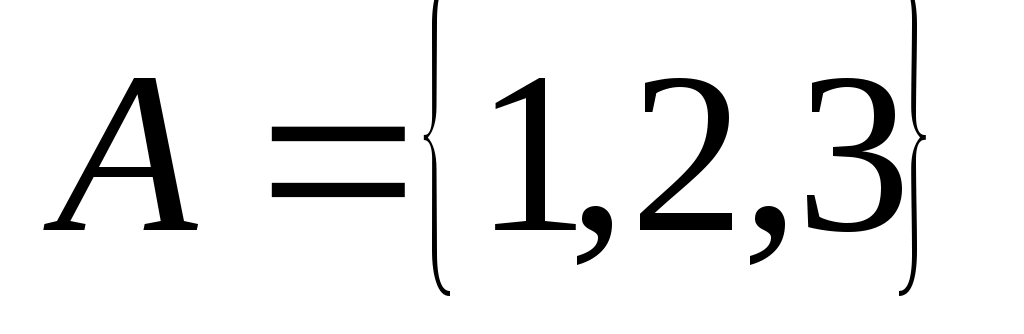 изображено на рис. 1.12. Его матрица имеет вид:
изображено на рис. 1.12. Его матрица имеет вид:
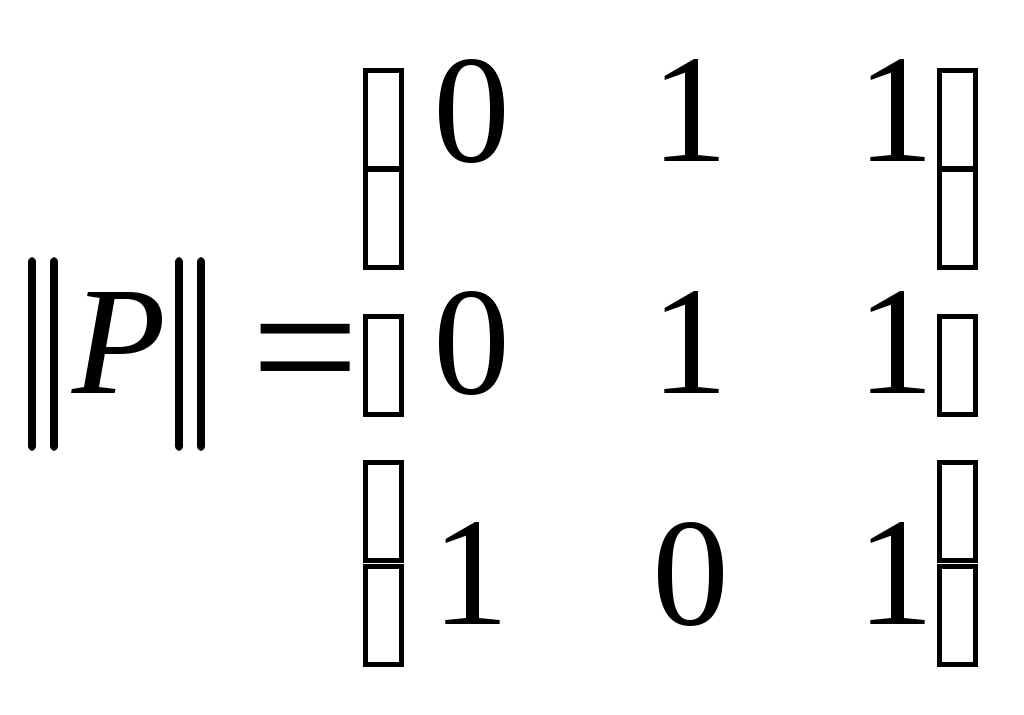 .
.
Пусть
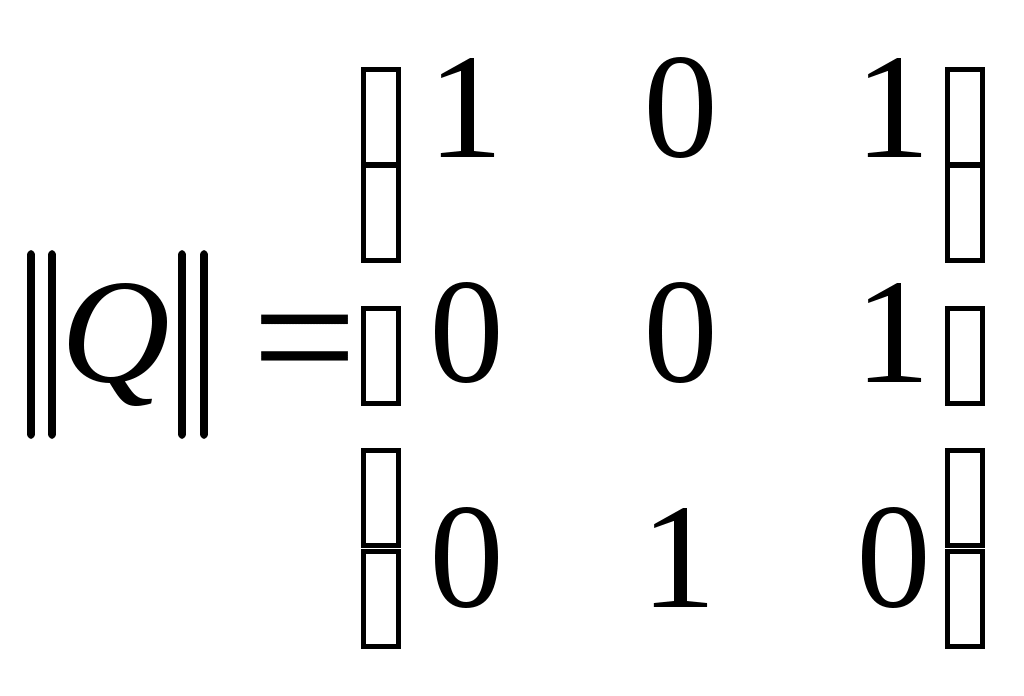 ,
,
тогда
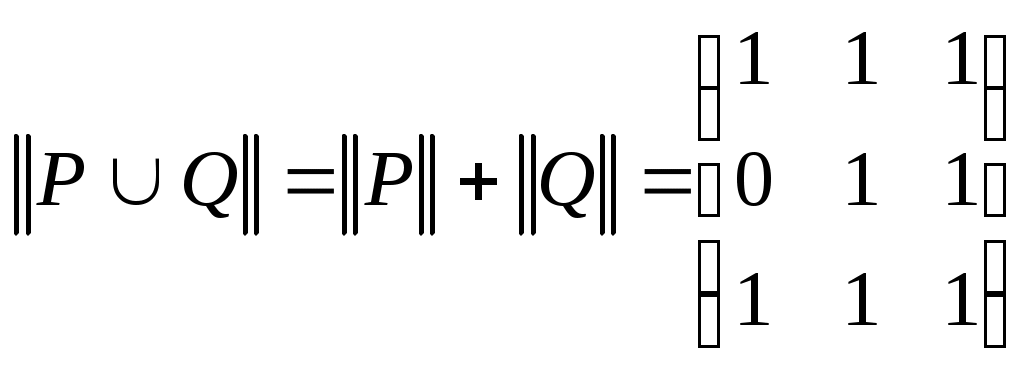 ,
, 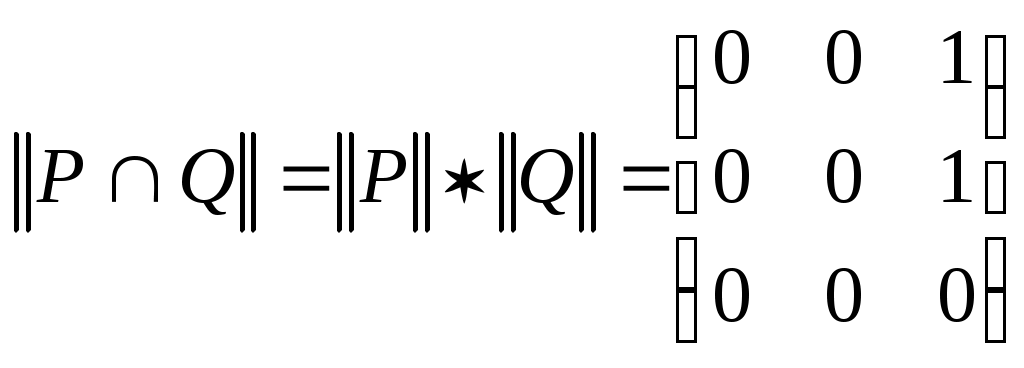 .
.
Р
ис. 1.12.
Бинарное отношение ,
, 
Пусть — бинарное отношение на множестве
— бинарное отношение на множестве  ,
, 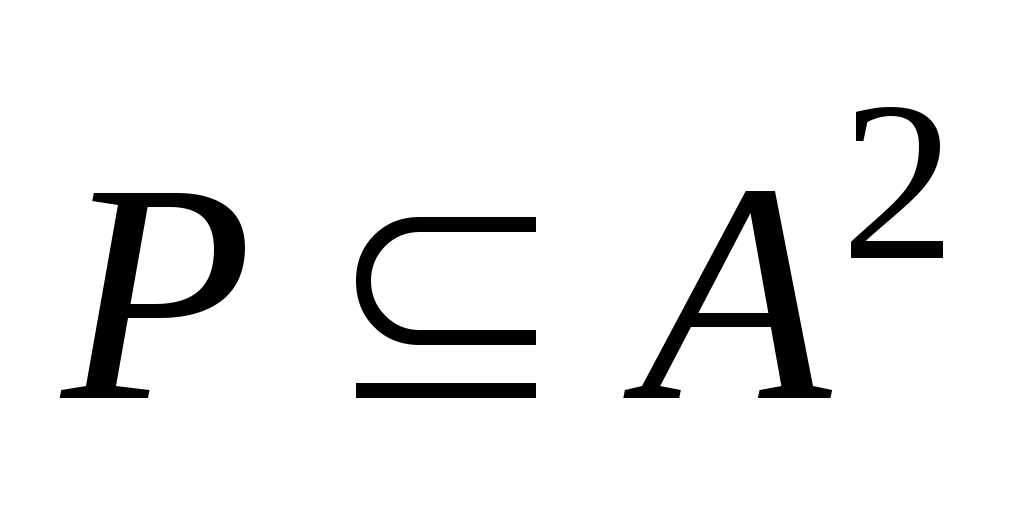 . Отношение
. Отношение  на множестве
на множестве  называется рефлексивным, если
называется рефлексивным, если 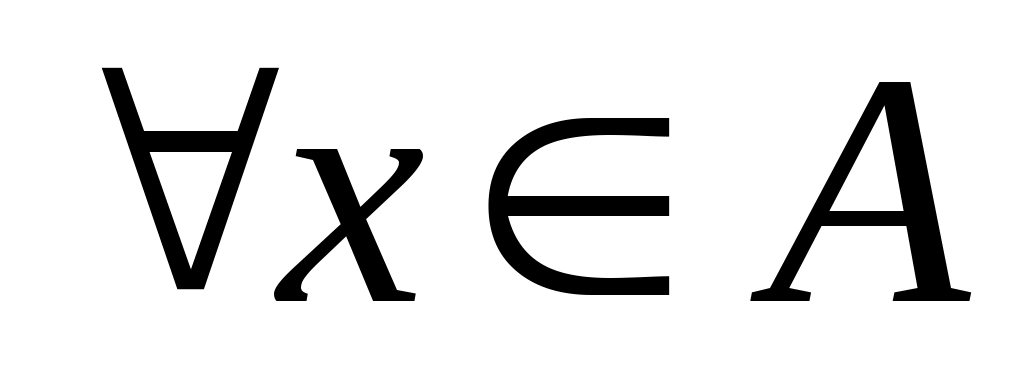 ,
,  , т. е.
, т. е.
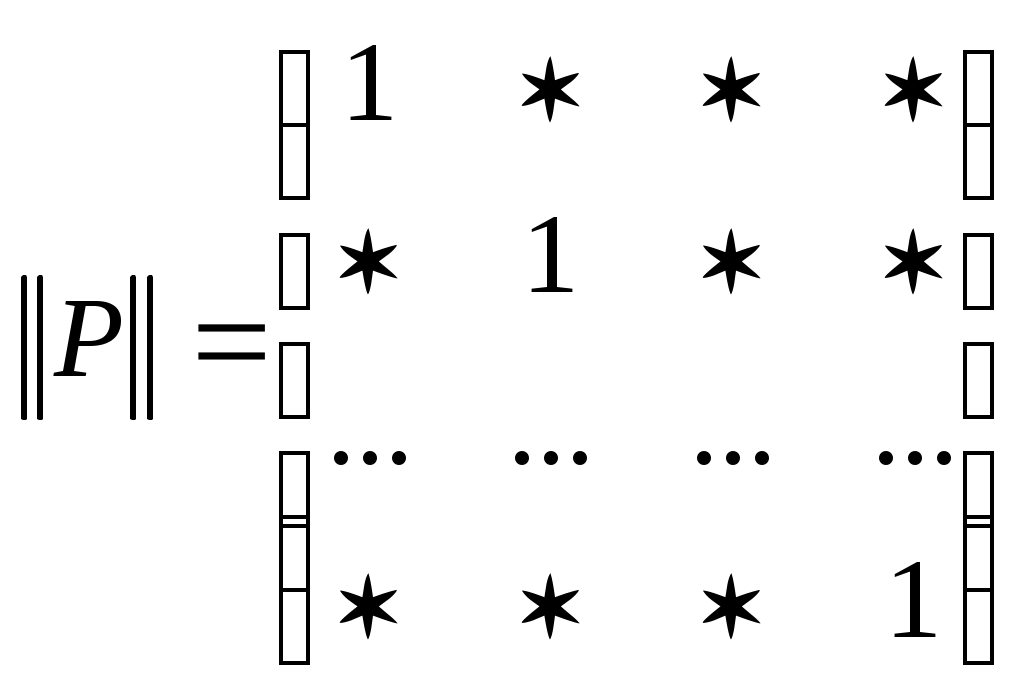 ,
,
где звездочкой обозначены нули или единицы. Отношение называется иррефлексивным, если
называется иррефлексивным, если 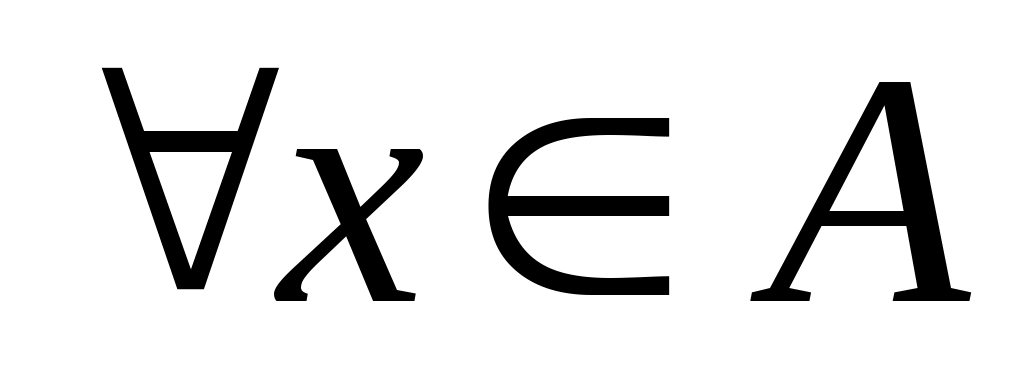 ,
, 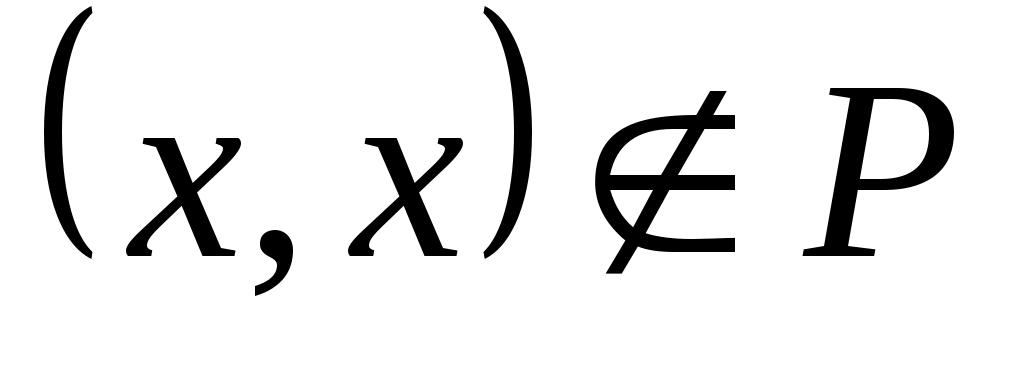 . Отношение
. Отношение  на множестве
на множестве  называется симметричным, если
называется симметричным, если 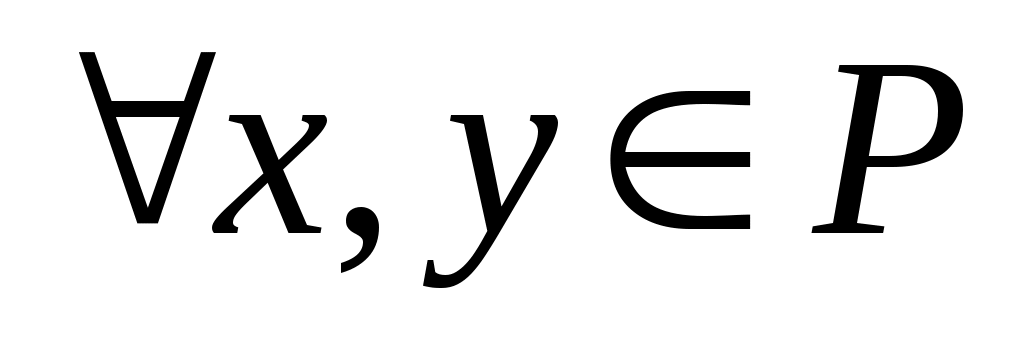 и из условия
и из условия  следует, что
следует, что  . Это значит, что
. Это значит, что  . Отношение
. Отношение  называется антисимметричным, если из условий
называется антисимметричным, если из условий  и
и  следует, что
следует, что 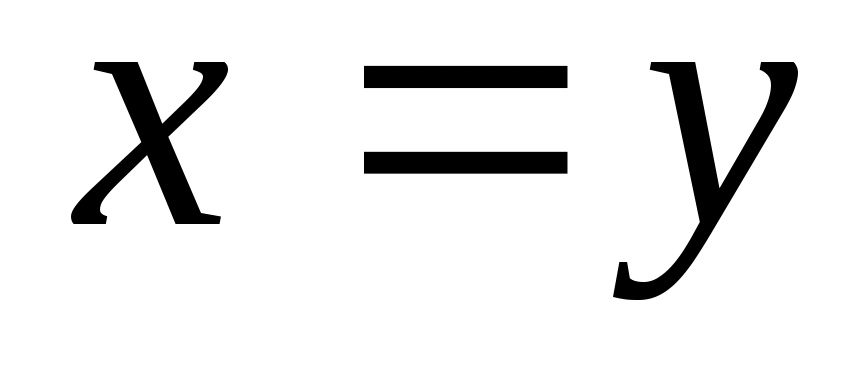 , или
, или 
. Это свойство приводит к тому, что у матрицы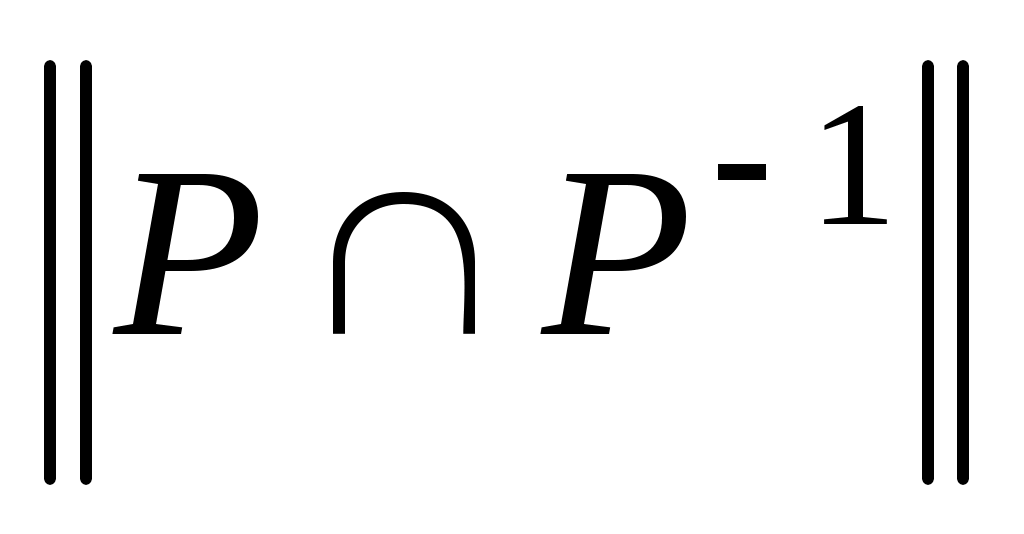 все элементы вне главной диагонали будут нулевыми (на главной диагонали тоже могут быть нули). Отношение
все элементы вне главной диагонали будут нулевыми (на главной диагонали тоже могут быть нули). Отношение  называется транзитивным, если из
называется транзитивным, если из  и
и 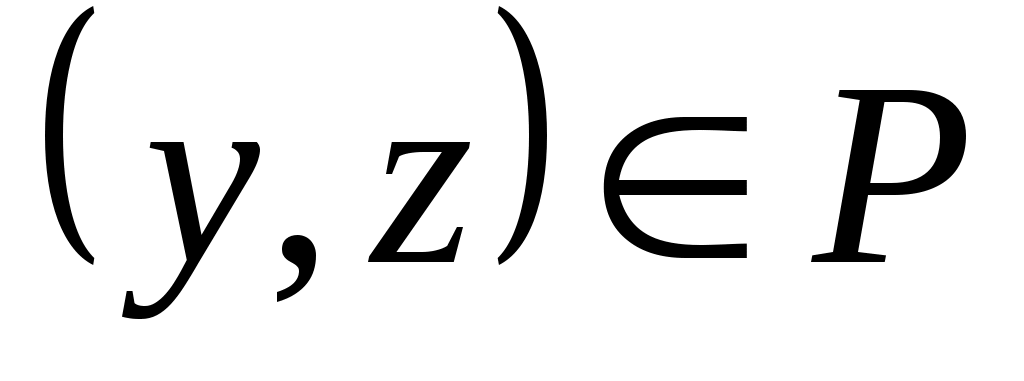 следует, что
следует, что 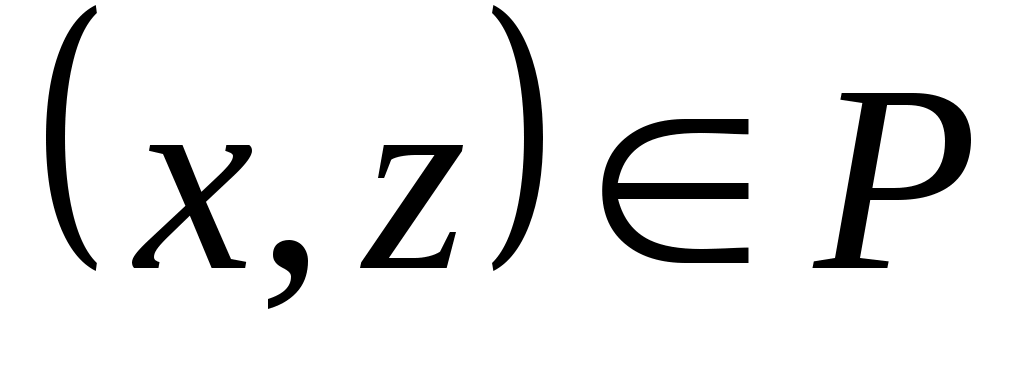 .
.
Рефлексивное, транзитивное и симметричное отношение на множестве называется эквивалентностью на
называется эквивалентностью на  . Эквивалентность обозначается символами
. Эквивалентность обозначается символами  или , например,
или , например, 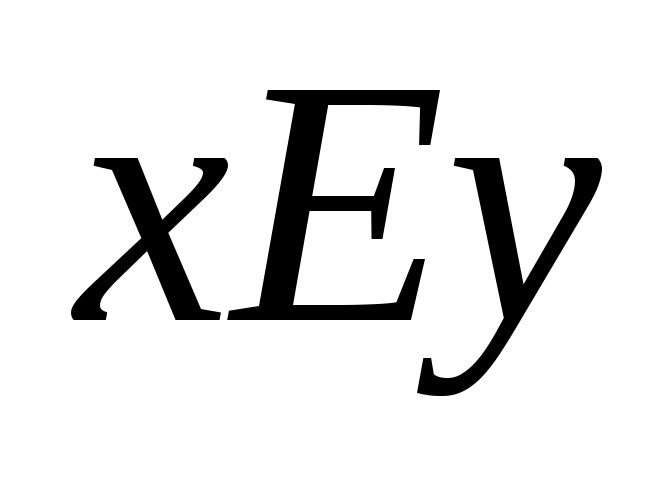 ,
,  .
.
Пример 2. Докажем, что на множестве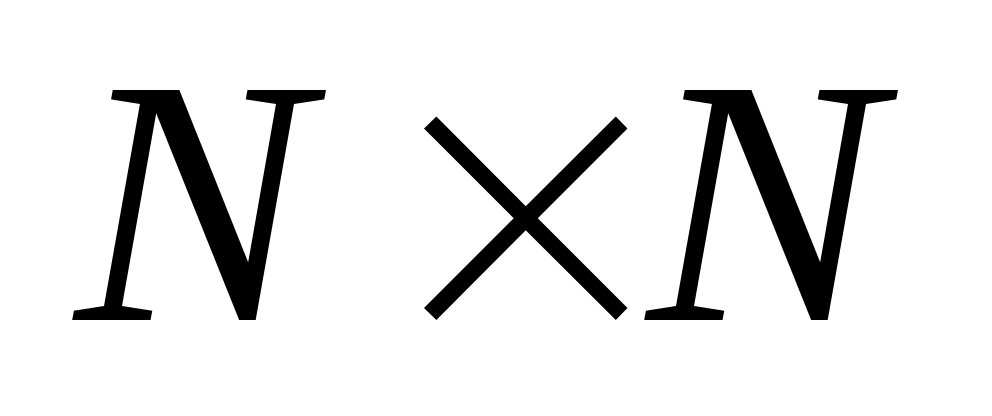 отношение
отношение  является отношением эквивалентности, если
является отношением эквивалентности, если 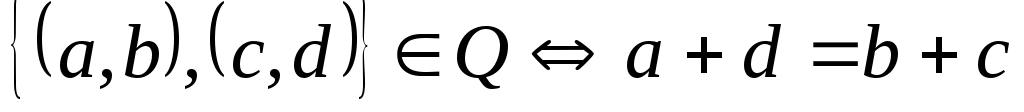 .
.
Если отношение рефлексивно на
рефлексивно на  , то
, то 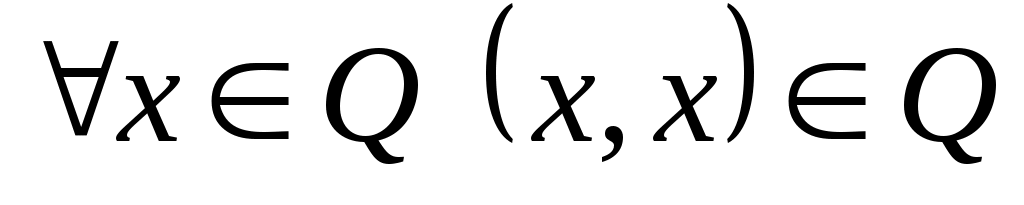 . В нашем случае роль
. В нашем случае роль  играет множество
играет множество 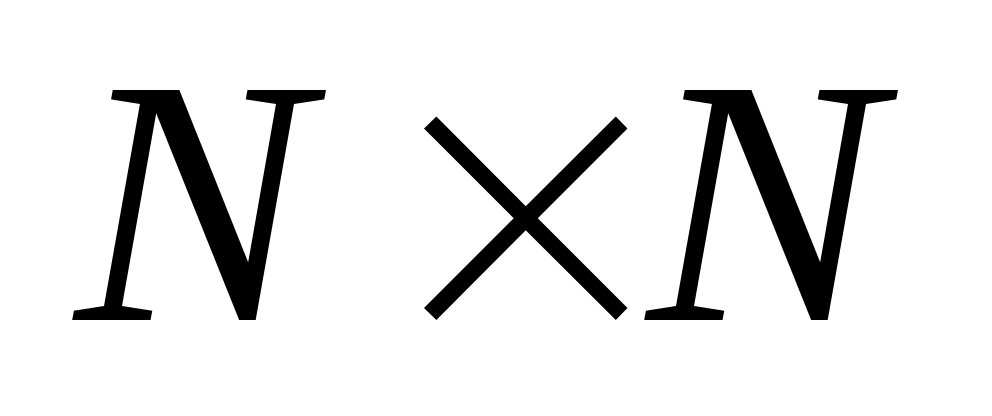 , а роль элемента
, а роль элемента  играет пара
играет пара 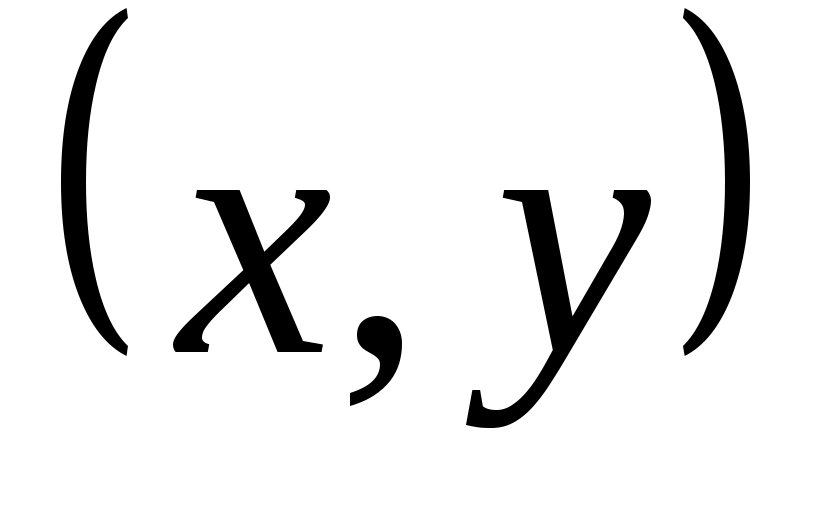 . Тогда отношение
. Тогда отношение  рефлексивно на
рефлексивно на 
, если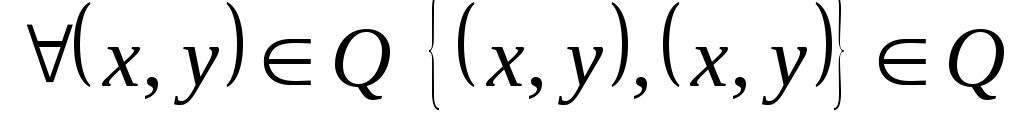 . По определению
. По определению 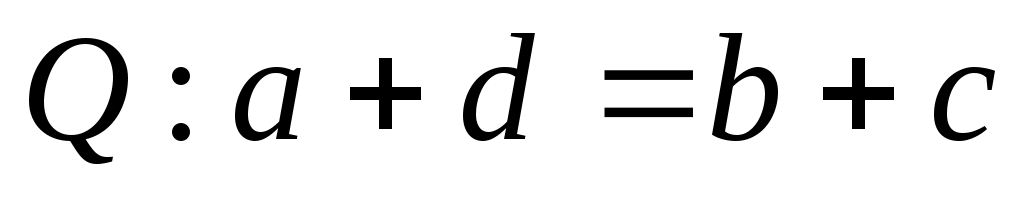 , но
, но 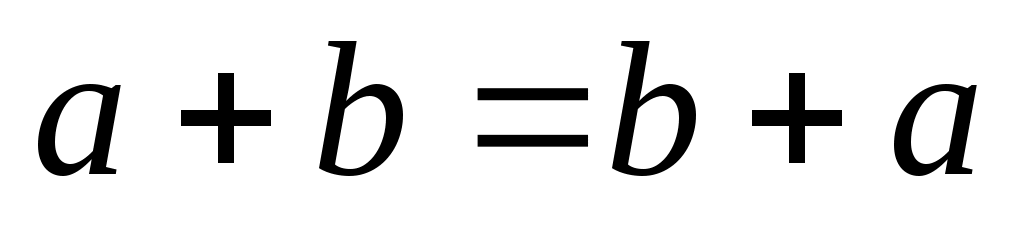 , следовательно,
, следовательно,  рефлексивно.
рефлексивно.
Аналогично, если , то и
, то и 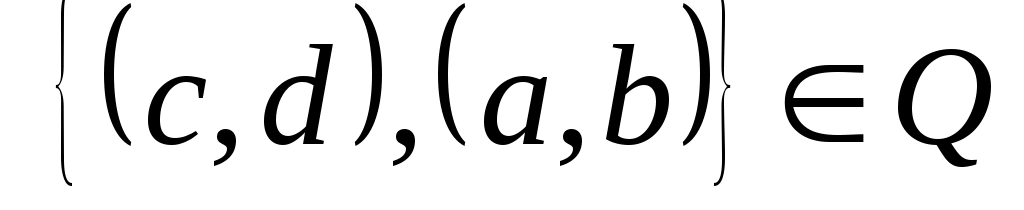 , так как из
, так как из 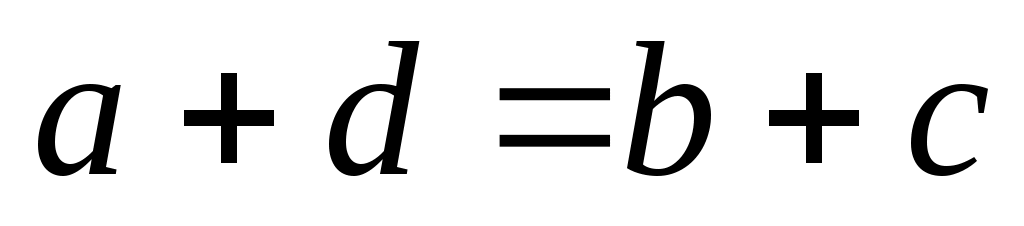 следует, что
следует, что 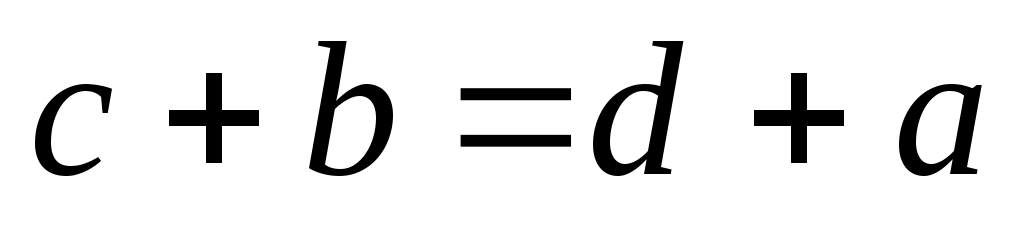 . Таким образом,
. Таким образом,  симметрично.
симметрично.
Наконец, если ,
,  , то
, то 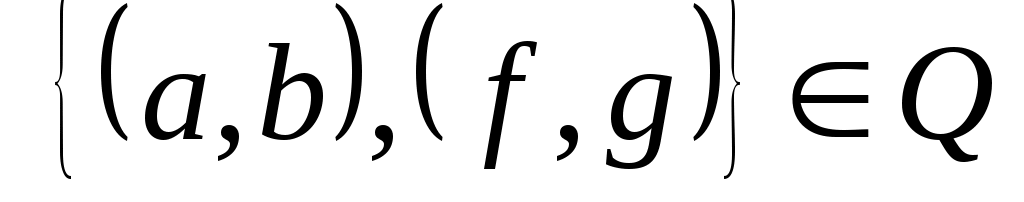 , так как
, так как 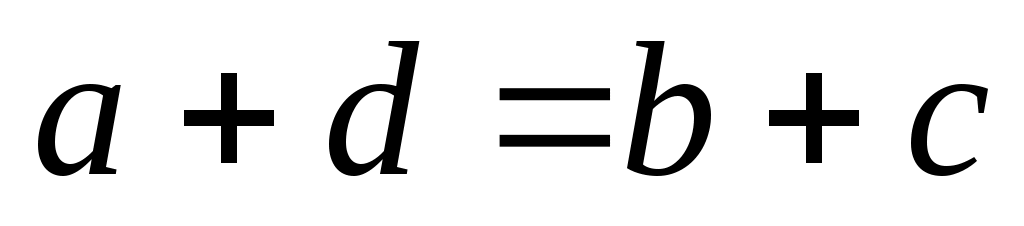 и
и 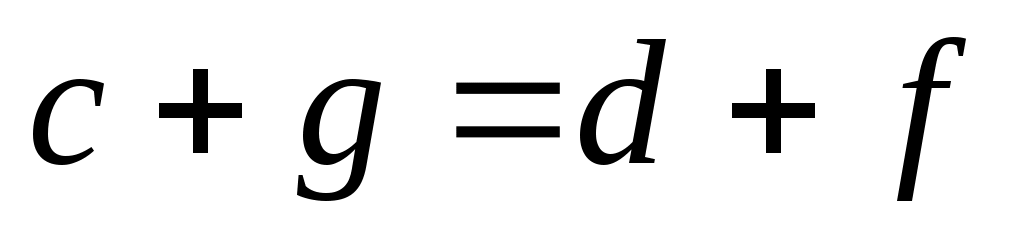 . Тогда
. Тогда 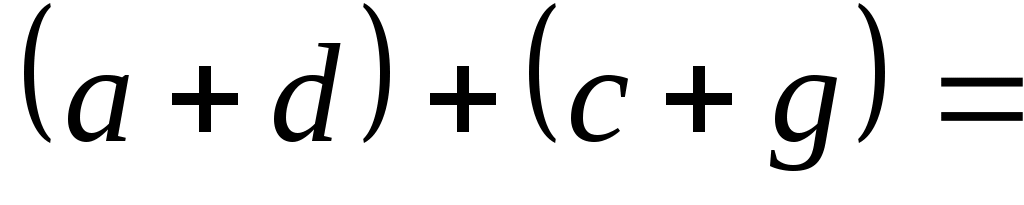
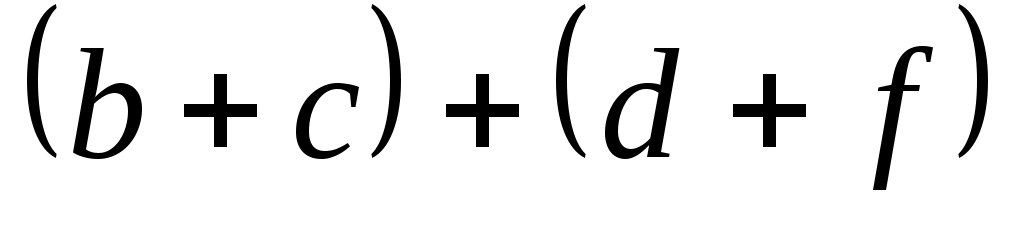
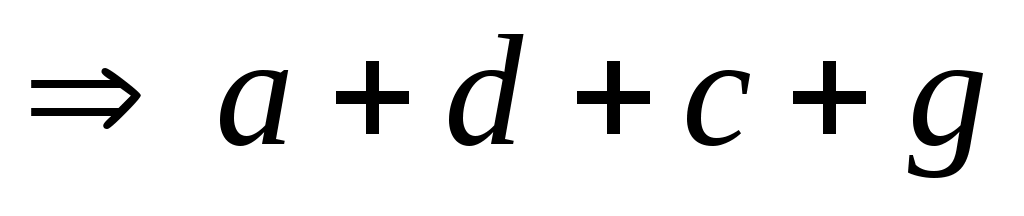
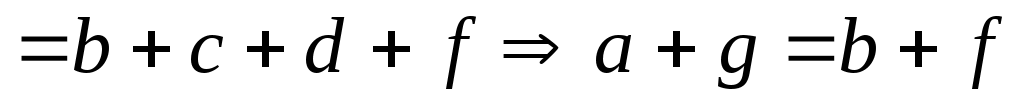 , т. е.
, т. е.  транзитивно.
транзитивно.
Рефлексивное, транзитивное и антисимметричное отношение на множестве называется частичным порядком на
называется частичным порядком на  . Частичный порядок обозначается символом
. Частичный порядок обозначается символом 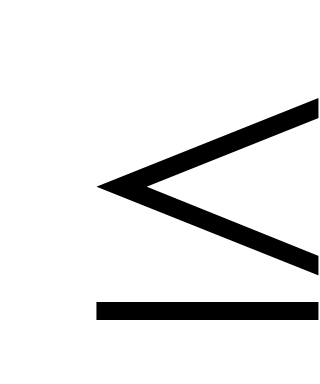 , а обратное ему отношение
, а обратное ему отношение 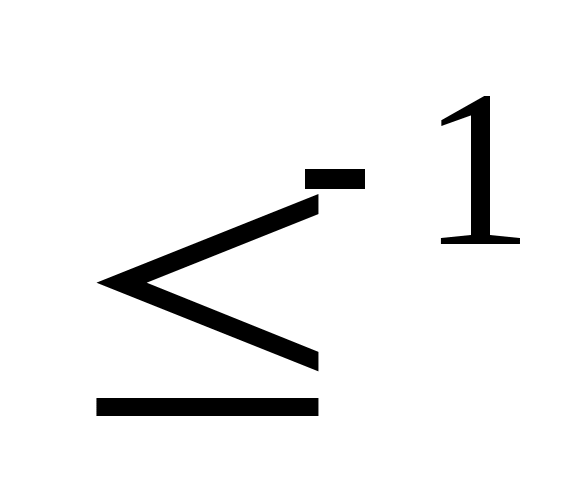 символом
символом 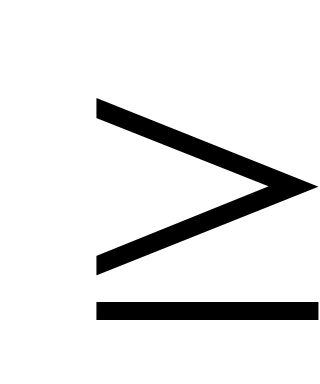 . Отношение
. Отношение 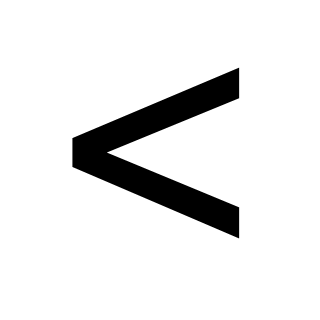
Часто элементы разных множеств связаны различными соотношениями, например, соотношениями порядка.
В теории множеств важную роль играют два вида специальных бинарных отношений: отношения эквивалентности и отношения порядка. Прообразами этих отношений служат интуитивные понятия равенства, предшествования и предпочтения.
Рассмотрим два конечных множества
следующим образом:
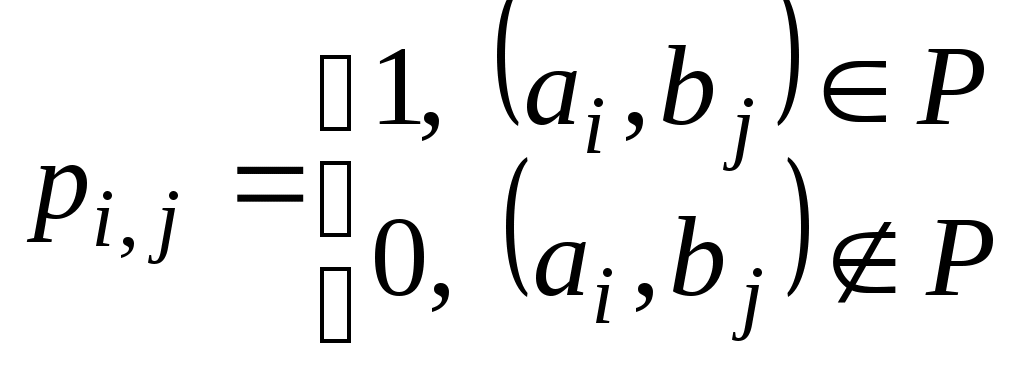 .
.Эта матрица содержит полную информацию о связях между элементами множеств
Матрица любого бинарного отношения обладает следующими свойствами:
-
если и
и 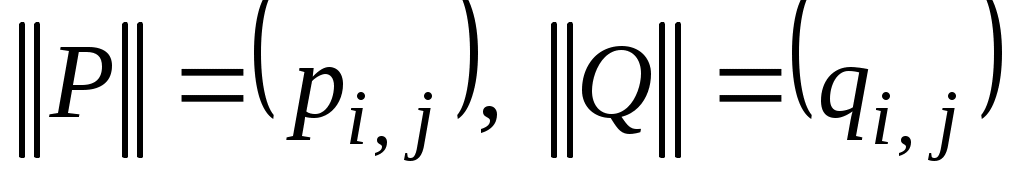 , то
, то  ;
; 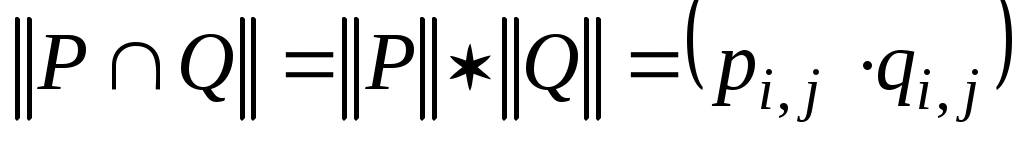 , причем сложение элементов матрицы осуществляется по правилам 0 + 0 = 0, 1 + 1 = 1, 1 + 0 = 0 + 1 = 1, а умножение осуществляется почленно обычным образом, т. е. по правилам
, причем сложение элементов матрицы осуществляется по правилам 0 + 0 = 0, 1 + 1 = 1, 1 + 0 = 0 + 1 = 1, а умножение осуществляется почленно обычным образом, т. е. по правилам 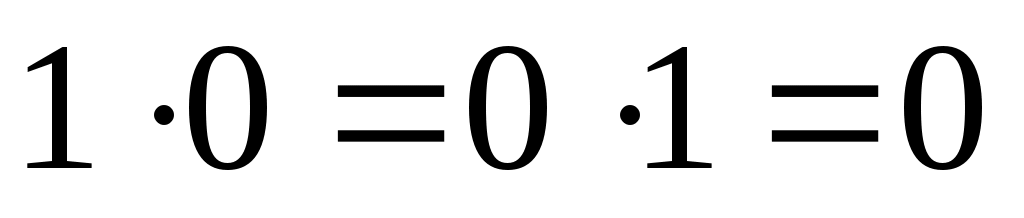 ,
, 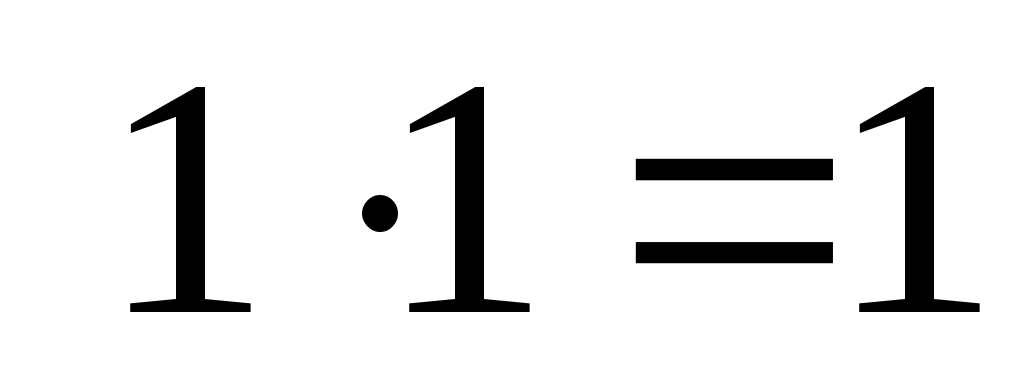 ;
; -
 , где
, где 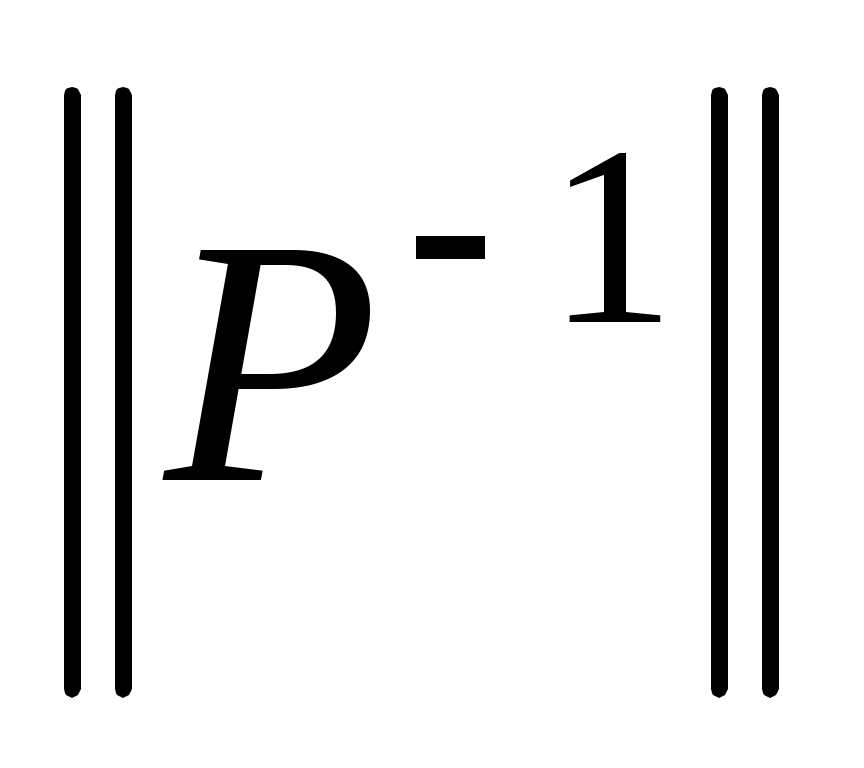 — матрица обратного отношения
— матрица обратного отношения 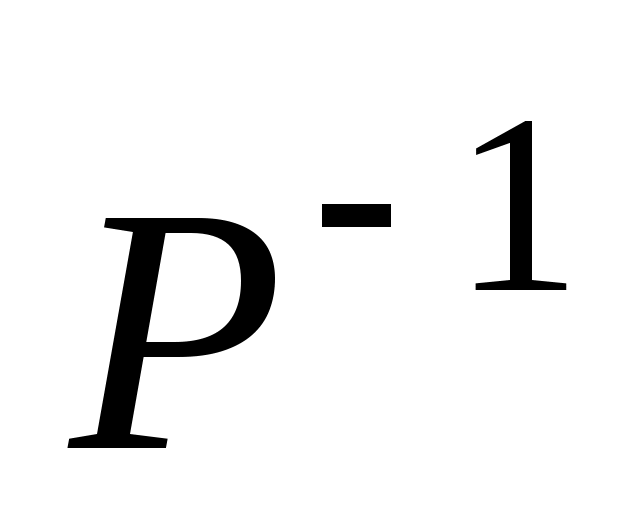 ;
; -
если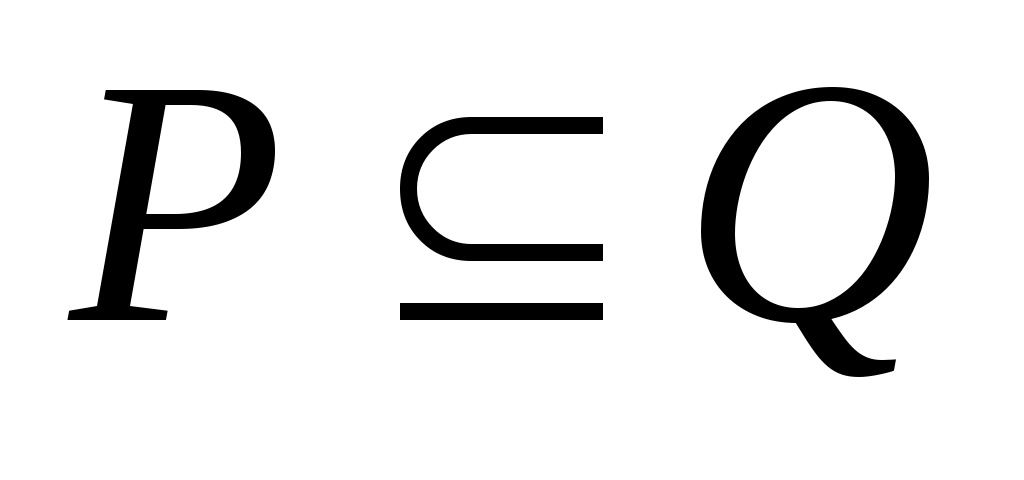 , то
, то 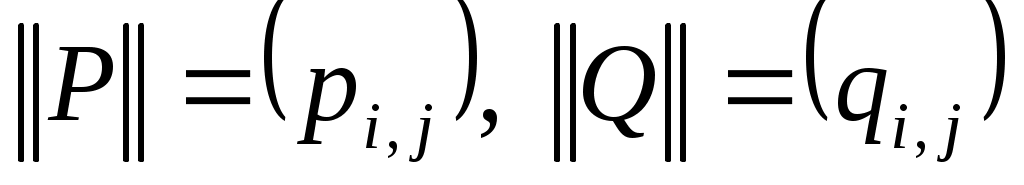 и
и  .
.
Пример 1. Бинарное отношение
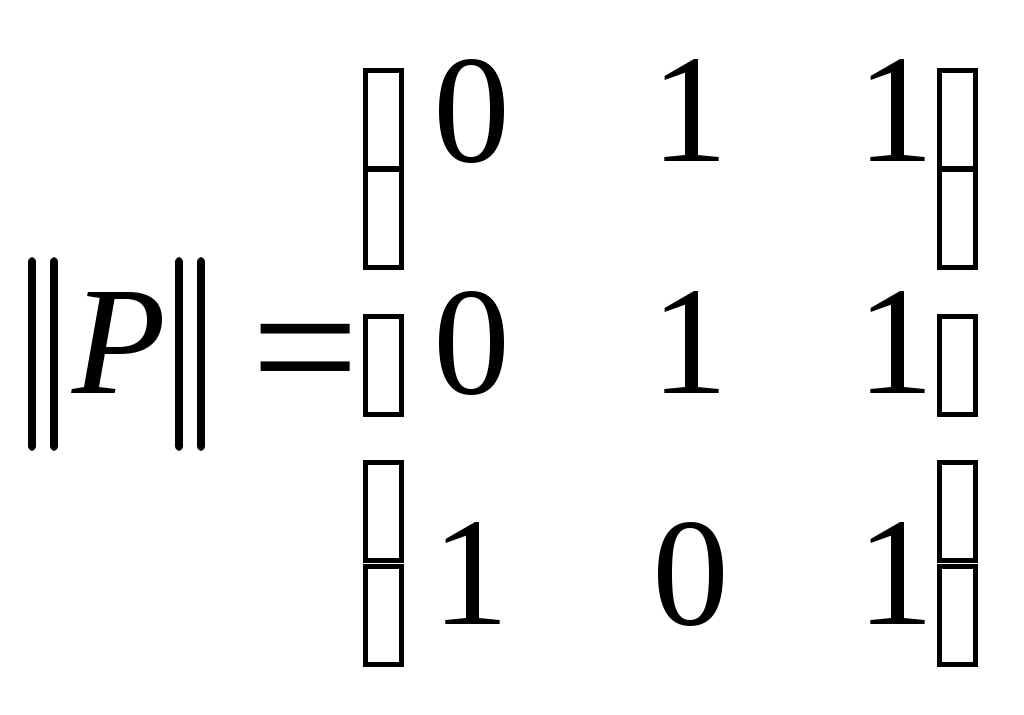 .
. Пусть
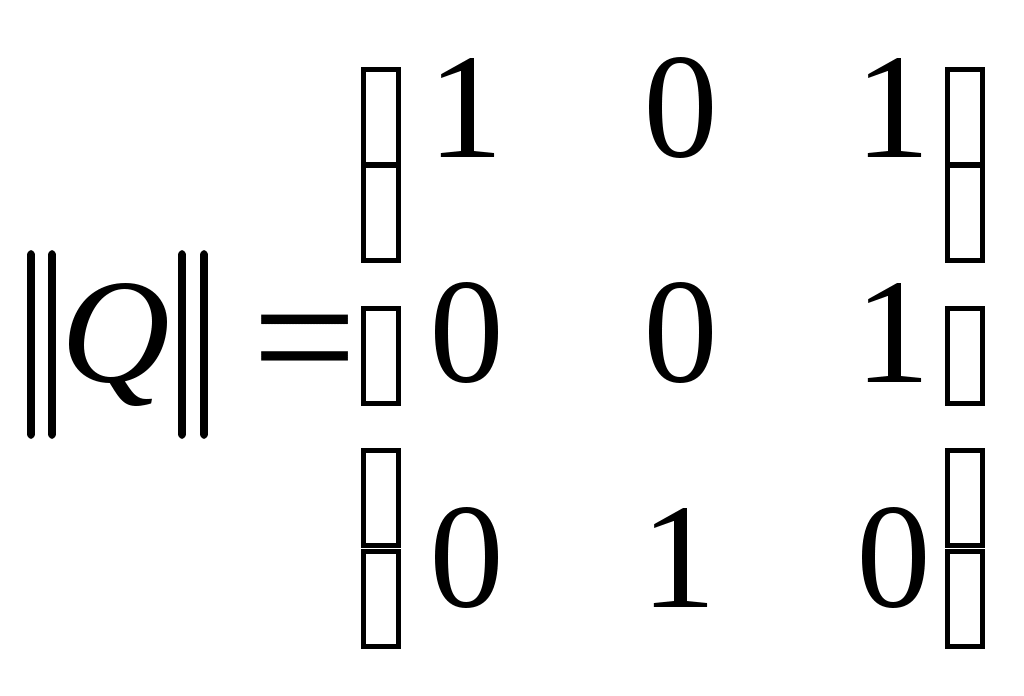 ,
,тогда
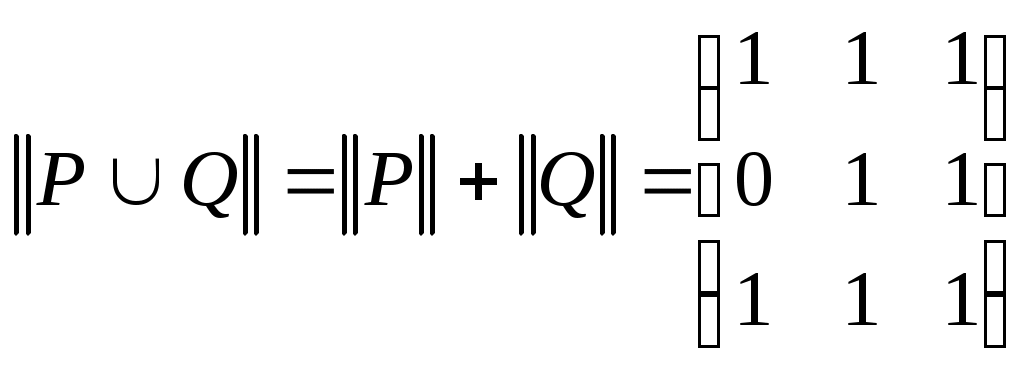 ,
, 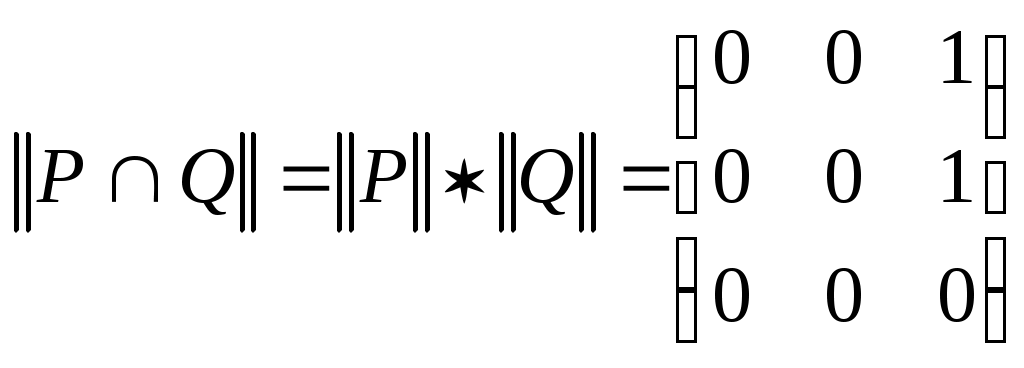 .
.Р

ис. 1.12.
Бинарное отношение
Пусть
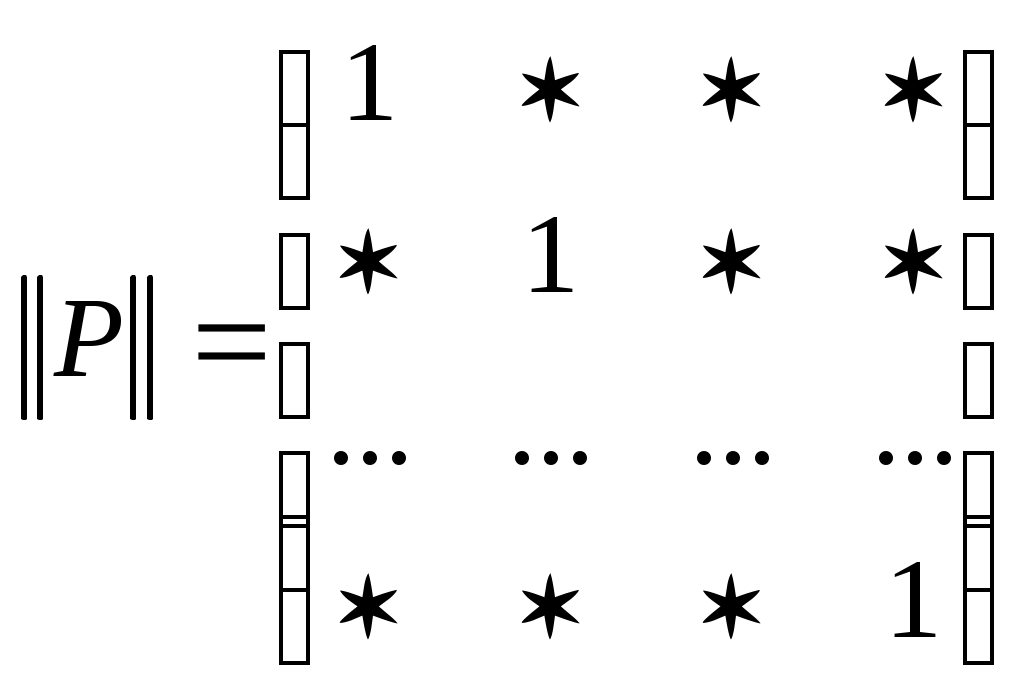 ,
,где звездочкой обозначены нули или единицы. Отношение
. Это свойство приводит к тому, что у матрицы
Рефлексивное, транзитивное и симметричное отношение на множестве
Пример 2. Докажем, что на множестве
Если отношение
, если
Аналогично, если
Наконец, если
Рефлексивное, транзитивное и антисимметричное отношение на множестве