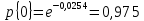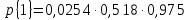Файл: Контрольная работа 1, 2 по дисциплине Организация управления в системе мчс Номер зачётной книжки 13134.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 90
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, вычисляемое по формуле (1.32), по данным для города оказалось следующим
D = (121,5)2 / (17,5∙937) = 0,854.
Таким образом, с помощью построенной по данным для города линейной функции тренда удается «объяснить» около 85,4 % общей вариации уровней динамического ряда числа пожаров за последние шесть лет. В последнем столбце табл. 1.9 представлены расчетные (сглаженные) значения уровней ряда, соответствующие построенной функции тренда.
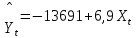(t = 1, 2, …, M) (1.33)
Производится построение графика динамики числа пожаров в городе за последние шесть лет. На график наносятся точки, соответствующие фактическим уровням динамического ряда, а также прямая линия, отображающая функцию тренда (1.33). Пример графика, построенного по данным для города Н., представлен на рис. 1.9. На графике просматривается тенденция роста числа пожаров в городе со временем.
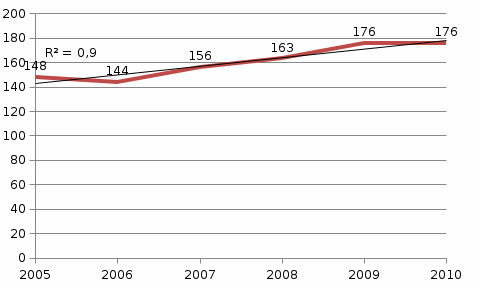
Рис. 1.9 . Динамика числа пожаров в городе за шесть лет и линия тренда, описывающая тенденцию ее развития
К задаче оценки тренда временного ряда примыкает задача прогнозирования, то есть продления в будущее (экстраполяция) тенденции развития временного ряда, наблюдавшейся в прошлом. При этом необходимо быть уверенным, что общие условия, определяющие тенденцию развития в прошлом, не претерпят существенных изменений в будущем.
Подставляя в модель (1.33) значение интервала времени (года) Xt, для которого производится прогноз (t = M+1, M+2,…) получают соответствующее ему прогнозируемое значение числа пожаров. Например, произведем прогноз для города Н. на 2011 г. (t = 7) и 2012 г. (t = 8):
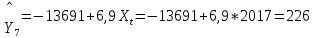
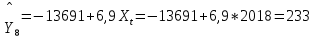
Таким образом, в городе в 2017 году следует ориентировочно ожидать 226 пожара, а в 2018 г. – 233 пожаров.
2. КОНТРОЛЬНАЯ РАБОТА 2
ТЕМА: ОЦЕНКА ВОЗМОЖНОСТЕЙ ОБСЛУЖИВАНИЯ ВЫЗОВОВ ПОЖАРНЫМИ ПОДРАЗДЕЛЕНИЯМИ В ГОРОДЕ НА ОСНОВЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Задание
По данным, полученным в результате выполнения контрольной работы 1, с применением метода математического моделирования обосновать количество оперативных отделений на основных пожарных автомобилях для надежной противопожарной защиты города по следующему плану:
1. Математическое моделирование процесса возникновения ситуаций одновременной занятости того или иного числа оперативных отделений на основных пожарных автомобилях обслуживанием вызовов в городе
2. Оценка возможностей обслуживания вызовов при том или ином заданном числе оперативных отделений на основных пожарных автомобилях в городе 3. Обоснование количества оперативных отделений на основных пожарных автомобилях, обеспечивающих надежную противопожарную защиту города
Методические указания к выполнению
Функционирование пожарных подразделений (ПП) в городе направлено на обслуживание возникающих вызовов. По каждому поступающему вызову производится высылка требуемого числа оперативных отделений на основных и на специальных пожарных автомобилях (ПА) к месту вызова (в дальнейшем рассматриваются оперативные отделения только на основных ПА). После выполнения боевой работы оперативные отделения возвращаются в свои депо.
Регистрация сведений о всех выездах ПП по вызовам осуществляется в диспетчерском журнале, который является основным источником первичных данных для изучения деятельности пожарной охраны по обслуживанию вызовов.
Поступающие вызовы имеют случайный характер по месту и времени их возникновения, по объему сил и средств пожарной охраны (числу оперативных отделений) и затратам времени, требуемым для их обслуживания. Вследствие этого в процессе функционирования ПП в городе могут возникать чрезвычайно напряженные ситуации, связанные с потребностью одновременного обслуживания нескольких вызовов и необходимостью привлечения для этих целей большого количества оперативных отделений.
Введем в рассмотрение возникающую в процессе функционирования ПП ситуацию {k}, в которой обслуживанием вызовов в городе одновременно занято некоторое число k ПА (k = 0, 1, 2,...). В качестве примера возникновения различных ситуаций рассмотрим представленный на рис. 2.1 фрагмент процесса поступления и обслуживания вызовов в городе
Н., которые соответствуют строкам 5, 6, 7 учебного диспетчерского журнала (табл.X.1).
По вызовам 5, 6 и 7 выезжает соответственно 1, 2 и 1 ПА. С 3 ч 47 м и до 4 ч 25 м происходит обслуживание вызова 5 силами 1 ПА, т.е. имеет место ситуация {1}. После 4 ч 25 м устанавливается ситуация {0}. В 4 ч 29 м приходит вызов 6, по которому выезжают 2 ПА. Таким образом, в этот момент возникает ситуация {2}. Однако вызов 7 поступает в 4 ч 38 м, когда обслуживание вызова 2 еще не закончено, и таким образом с этого момента одновременно обслуживаются два вызова, на которых оказываются занятыми в сумме 3 ПА (т.е. имеет место ситуация {3}). Ситуация {3} длится до 4 ч 54 м, когда обслуживание вызова 6 заканчивается.
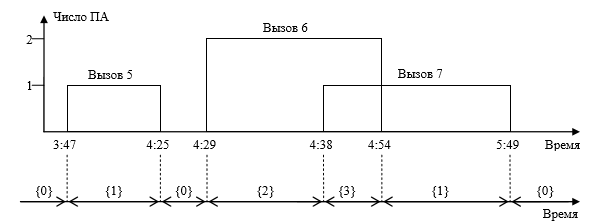
Рис. 2.1. Схематическое изображение фрагмента процесса одновременной занятости пожарных подразделений обслуживанием вызовов в городе
Изучение возможностей возникновения различных ситуаций {k} одновременной занятости того или иного числа k ПА (k = 0, 1, 2,...) обслуживанием вызовов в городе удобно производить путем математического моделирования процесса функционирования ПП в городе.
На процесс функционирования ПП оказывает влияние огромное количество факторов, случайных по своей природе, поэтому присущие этому процессу закономерности имеют вероятностный характер. Эти закономерности достаточно хорошо изучены и для их количественного описания построены математические модели, описывающие различные аспекты функционирования ПП в городе. С точки зрения поставленной задачи, интерес представляет вероятностная модель, описывающая процесс возникновения ситуаций одновременной занятости того или иного числа оперативных отделений обслуживанием вызовов в городе. Оценка параметров модели производится по статистическим данным о вызовах ПП для конкретного города. Моделирование сводится к расчетам вероятностных, временных и частотных характеристик процесса возникновения различных ситуаций {k} одновременной занятости того или иного числа k ПА (k = 0, 1, 2,...) обслуживанием вызовов в городе.
Полученные результаты моделирования служат исходной базой для дальнейших расчетов по оценке возможностей обслуживания вызовов в городе при наличии в нем того или иного числа N ПА. Оценка осуществляется с точки зрения безотказности обслуживания вызовов.
Отказ понимается как событие, которое состоит в том, что по очередному вызову не может выехать требуемое число ПА вследствие их занятости обслуживанием ранее поступивших вызовов (недостающее число ПА приходится дополнительно привлекать извне города или из резерва, что нежелательно, так как связано с организационными трудностями и большими затратами времени). Отказ называется полным, если по вызову не может выехать ни один ПА. Отказ называется частичным, если по вызову может выехать число ПА меньшее, чем требуется для его обслуживания.
Отказы связаны с возникновением в процессе функционирования ПП в городе ситуации {>N}, в которой заданного числа N ПА недостаточно для обслуживания вызовов (т.е. требуемое для одновременного обслуживания вызовов число ПА превышает заданное число N).
Математическое моделирование дает возможность рассчитать частотные, вероятностные и временные характеристики процесса возникновения различных ситуаций {>N} при том или ином заданном числе N ПА (N = 0, 1, 2,...) в городе. Результаты моделирования находят полезное применение для обоснования требуемого количества ПА, обеспечивающих надежную противопожарную защиту города.
В контрольной работе 2 требуется, исходя из формализованной в виде модельных соотношений информации об известных закономерностях случайных процессов поступления и обслуживания вызовов, а также из доступной информации, используемой для оценки параметров модели, расчетным путем получить информацию о возможностях того или иного заданного числа ПА обслуживать вызовы в городе. По результатам расчетов следует осуществить обоснованный выбор количества оперативных отделений на основных ПА для надежной защиты города.
1. Математическое моделирование процесса возникновения ситуаций одновременной занятости того или иного числа оперативных отделений на основных пожарных автомобилях обслуживанием вызовов в городе
Для построения вероятностной модели, описывающей процесс возникновения ситуаций одновременной занятости того или иного числа оперативных отделений обслуживанием вызовов в городе, необходимо определить параметры этой модели:
– интенсивность потока вызовов ПП в городе (λ) вычислена в контрольной работе 1 (пункт 3) по формуле (1.8), исходя из общего числа n вызовов ПП в городе за период времени наблюдения Tнабл = 1 год = 8760 ч;
– значение средней продолжительности времени обслуживания вызова ПП в городе (τобс
) представлено в табл. X.9 исходных данных;
– значения долей (относительных частот) ωl (l = 1, 2,..., L), которые в общем числе вызовов составляют вызовы с привлечением для их обслуживания того или иного числаl ПА, вычислены в контрольной работе 1 (пункт 1) по формуле (1.2) и представлены в табл. 1.1.
Например, перечисленные параметры модели по данным для города оказались следующими: λ = 328 (вызовов/год) = 0,899 (вызовов/сут) = 0,0374 (вызовов/ч);
= 40,8 (мин/вызов) = 0,68 (ч/вызов);
ω1 = 0,518; ω2 = 0,287; ω3 = 0,149; ω4 = 0,046.
Исходя из λ значений и =, оценивается параметр ɑ, называемый приведенной интенсивностью потока вызовов ПП в городе:
ɑ = λ · (2.1)
Приведенная интенсивность потока вызовов ПП показывает, сколько вызовов в среднем возникает на интервале времени, равном средней продолжительности времени обслуживания одного вызова.
Например, приведенная интенсивность потока вызовов ПП по данным для города оценивается следующим образом:
ɑ = 0,0374 · 0,68 = 0,0254
Исходя из оценок параметров модели, осуществляется математическое моделирование процесса возникновения различных ситуаций {k} одновременной занятости того или иного числа kПА (k = 0, 1, 2,...) обслуживанием вызовов в городе. Моделирование сводится к расчетам вероятностных, временных и частотных характеристик изучаемого процесса.
Вычисляется вероятность p{0} того, что в произвольный момент времени обслуживанием вызовов в городе не занято ни одного ПА (т.е. имеет место ситуация {0}):
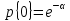(2.2)
где e = 2,71828 – основание натурального логарифма.
Вероятность p{k} того, что в произвольный момент времени обслуживанием вызовов в городе будут одновременно заняты k ПА (т.е. имеет место ситуация {k}), вычисляется последовательно для k = 1, 2, 3, 4,... c помощью рекуррентной формулы
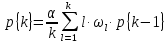(k = 1, 2, 3,4) (2.3)
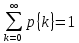(2.4)
Производя вычисления по формулам (2.2) и (2.3) для города, получаем:
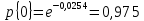
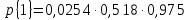
D = (121,5)2 / (17,5∙937) = 0,854.
Таким образом, с помощью построенной по данным для города линейной функции тренда удается «объяснить» около 85,4 % общей вариации уровней динамического ряда числа пожаров за последние шесть лет. В последнем столбце табл. 1.9 представлены расчетные (сглаженные) значения уровней ряда, соответствующие построенной функции тренда.
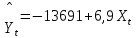(t = 1, 2, …, M) (1.33)Производится построение графика динамики числа пожаров в городе за последние шесть лет. На график наносятся точки, соответствующие фактическим уровням динамического ряда, а также прямая линия, отображающая функцию тренда (1.33). Пример графика, построенного по данным для города Н., представлен на рис. 1.9. На графике просматривается тенденция роста числа пожаров в городе со временем.
Рис. 1.9 . Динамика числа пожаров в городе за шесть лет и линия тренда, описывающая тенденцию ее развития
К задаче оценки тренда временного ряда примыкает задача прогнозирования, то есть продления в будущее (экстраполяция) тенденции развития временного ряда, наблюдавшейся в прошлом. При этом необходимо быть уверенным, что общие условия, определяющие тенденцию развития в прошлом, не претерпят существенных изменений в будущем.
Подставляя в модель (1.33) значение интервала времени (года) Xt, для которого производится прогноз (t = M+1, M+2,…) получают соответствующее ему прогнозируемое значение числа пожаров. Например, произведем прогноз для города Н. на 2011 г. (t = 7) и 2012 г. (t = 8):
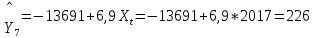
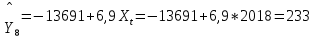
Таким образом, в городе в 2017 году следует ориентировочно ожидать 226 пожара, а в 2018 г. – 233 пожаров.
2. КОНТРОЛЬНАЯ РАБОТА 2
ТЕМА: ОЦЕНКА ВОЗМОЖНОСТЕЙ ОБСЛУЖИВАНИЯ ВЫЗОВОВ ПОЖАРНЫМИ ПОДРАЗДЕЛЕНИЯМИ В ГОРОДЕ НА ОСНОВЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Задание
По данным, полученным в результате выполнения контрольной работы 1, с применением метода математического моделирования обосновать количество оперативных отделений на основных пожарных автомобилях для надежной противопожарной защиты города по следующему плану:
1. Математическое моделирование процесса возникновения ситуаций одновременной занятости того или иного числа оперативных отделений на основных пожарных автомобилях обслуживанием вызовов в городе
2. Оценка возможностей обслуживания вызовов при том или ином заданном числе оперативных отделений на основных пожарных автомобилях в городе 3. Обоснование количества оперативных отделений на основных пожарных автомобилях, обеспечивающих надежную противопожарную защиту города
Методические указания к выполнению
Функционирование пожарных подразделений (ПП) в городе направлено на обслуживание возникающих вызовов. По каждому поступающему вызову производится высылка требуемого числа оперативных отделений на основных и на специальных пожарных автомобилях (ПА) к месту вызова (в дальнейшем рассматриваются оперативные отделения только на основных ПА). После выполнения боевой работы оперативные отделения возвращаются в свои депо.
Регистрация сведений о всех выездах ПП по вызовам осуществляется в диспетчерском журнале, который является основным источником первичных данных для изучения деятельности пожарной охраны по обслуживанию вызовов.
Поступающие вызовы имеют случайный характер по месту и времени их возникновения, по объему сил и средств пожарной охраны (числу оперативных отделений) и затратам времени, требуемым для их обслуживания. Вследствие этого в процессе функционирования ПП в городе могут возникать чрезвычайно напряженные ситуации, связанные с потребностью одновременного обслуживания нескольких вызовов и необходимостью привлечения для этих целей большого количества оперативных отделений.
Введем в рассмотрение возникающую в процессе функционирования ПП ситуацию {k}, в которой обслуживанием вызовов в городе одновременно занято некоторое число k ПА (k = 0, 1, 2,...). В качестве примера возникновения различных ситуаций рассмотрим представленный на рис. 2.1 фрагмент процесса поступления и обслуживания вызовов в городе
Н., которые соответствуют строкам 5, 6, 7 учебного диспетчерского журнала (табл.X.1).
По вызовам 5, 6 и 7 выезжает соответственно 1, 2 и 1 ПА. С 3 ч 47 м и до 4 ч 25 м происходит обслуживание вызова 5 силами 1 ПА, т.е. имеет место ситуация {1}. После 4 ч 25 м устанавливается ситуация {0}. В 4 ч 29 м приходит вызов 6, по которому выезжают 2 ПА. Таким образом, в этот момент возникает ситуация {2}. Однако вызов 7 поступает в 4 ч 38 м, когда обслуживание вызова 2 еще не закончено, и таким образом с этого момента одновременно обслуживаются два вызова, на которых оказываются занятыми в сумме 3 ПА (т.е. имеет место ситуация {3}). Ситуация {3} длится до 4 ч 54 м, когда обслуживание вызова 6 заканчивается.
Рис. 2.1. Схематическое изображение фрагмента процесса одновременной занятости пожарных подразделений обслуживанием вызовов в городе
Изучение возможностей возникновения различных ситуаций {k} одновременной занятости того или иного числа k ПА (k = 0, 1, 2,...) обслуживанием вызовов в городе удобно производить путем математического моделирования процесса функционирования ПП в городе.
На процесс функционирования ПП оказывает влияние огромное количество факторов, случайных по своей природе, поэтому присущие этому процессу закономерности имеют вероятностный характер. Эти закономерности достаточно хорошо изучены и для их количественного описания построены математические модели, описывающие различные аспекты функционирования ПП в городе. С точки зрения поставленной задачи, интерес представляет вероятностная модель, описывающая процесс возникновения ситуаций одновременной занятости того или иного числа оперативных отделений обслуживанием вызовов в городе. Оценка параметров модели производится по статистическим данным о вызовах ПП для конкретного города. Моделирование сводится к расчетам вероятностных, временных и частотных характеристик процесса возникновения различных ситуаций {k} одновременной занятости того или иного числа k ПА (k = 0, 1, 2,...) обслуживанием вызовов в городе.
Полученные результаты моделирования служат исходной базой для дальнейших расчетов по оценке возможностей обслуживания вызовов в городе при наличии в нем того или иного числа N ПА. Оценка осуществляется с точки зрения безотказности обслуживания вызовов.
Отказ понимается как событие, которое состоит в том, что по очередному вызову не может выехать требуемое число ПА вследствие их занятости обслуживанием ранее поступивших вызовов (недостающее число ПА приходится дополнительно привлекать извне города или из резерва, что нежелательно, так как связано с организационными трудностями и большими затратами времени). Отказ называется полным, если по вызову не может выехать ни один ПА. Отказ называется частичным, если по вызову может выехать число ПА меньшее, чем требуется для его обслуживания.
Отказы связаны с возникновением в процессе функционирования ПП в городе ситуации {>N}, в которой заданного числа N ПА недостаточно для обслуживания вызовов (т.е. требуемое для одновременного обслуживания вызовов число ПА превышает заданное число N).
Математическое моделирование дает возможность рассчитать частотные, вероятностные и временные характеристики процесса возникновения различных ситуаций {>N} при том или ином заданном числе N ПА (N = 0, 1, 2,...) в городе. Результаты моделирования находят полезное применение для обоснования требуемого количества ПА, обеспечивающих надежную противопожарную защиту города.
В контрольной работе 2 требуется, исходя из формализованной в виде модельных соотношений информации об известных закономерностях случайных процессов поступления и обслуживания вызовов, а также из доступной информации, используемой для оценки параметров модели, расчетным путем получить информацию о возможностях того или иного заданного числа ПА обслуживать вызовы в городе. По результатам расчетов следует осуществить обоснованный выбор количества оперативных отделений на основных ПА для надежной защиты города.
1. Математическое моделирование процесса возникновения ситуаций одновременной занятости того или иного числа оперативных отделений на основных пожарных автомобилях обслуживанием вызовов в городе
Для построения вероятностной модели, описывающей процесс возникновения ситуаций одновременной занятости того или иного числа оперативных отделений обслуживанием вызовов в городе, необходимо определить параметры этой модели:
– интенсивность потока вызовов ПП в городе (λ) вычислена в контрольной работе 1 (пункт 3) по формуле (1.8), исходя из общего числа n вызовов ПП в городе за период времени наблюдения Tнабл = 1 год = 8760 ч;
– значение средней продолжительности времени обслуживания вызова ПП в городе (τобс
) представлено в табл. X.9 исходных данных;
– значения долей (относительных частот) ωl (l = 1, 2,..., L), которые в общем числе вызовов составляют вызовы с привлечением для их обслуживания того или иного числаl ПА, вычислены в контрольной работе 1 (пункт 1) по формуле (1.2) и представлены в табл. 1.1.
Например, перечисленные параметры модели по данным для города оказались следующими: λ = 328 (вызовов/год) = 0,899 (вызовов/сут) = 0,0374 (вызовов/ч);
= 40,8 (мин/вызов) = 0,68 (ч/вызов); ω1 = 0,518; ω2 = 0,287; ω3 = 0,149; ω4 = 0,046.
Исходя из λ значений и
=, оценивается параметр ɑ, называемый приведенной интенсивностью потока вызовов ПП в городе:ɑ = λ ·
(2.1)Приведенная интенсивность потока вызовов ПП показывает, сколько вызовов в среднем возникает на интервале времени, равном средней продолжительности времени обслуживания одного вызова.
Например, приведенная интенсивность потока вызовов ПП по данным для города оценивается следующим образом:
ɑ = 0,0374 · 0,68 = 0,0254
Исходя из оценок параметров модели, осуществляется математическое моделирование процесса возникновения различных ситуаций {k} одновременной занятости того или иного числа kПА (k = 0, 1, 2,...) обслуживанием вызовов в городе. Моделирование сводится к расчетам вероятностных, временных и частотных характеристик изучаемого процесса.
Вычисляется вероятность p{0} того, что в произвольный момент времени обслуживанием вызовов в городе не занято ни одного ПА (т.е. имеет место ситуация {0}):
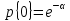(2.2)где e = 2,71828 – основание натурального логарифма.
Вероятность p{k} того, что в произвольный момент времени обслуживанием вызовов в городе будут одновременно заняты k ПА (т.е. имеет место ситуация {k}), вычисляется последовательно для k = 1, 2, 3, 4,... c помощью рекуррентной формулы
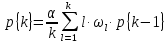(k = 1, 2, 3,4) (2.3) 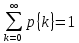(2.4)Производя вычисления по формулам (2.2) и (2.3) для города, получаем: