Файл: Контрольная работа 1, 2 по дисциплине Организация управления в системе мчс Номер зачётной книжки 13134.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 92
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1.4. Анализ изменчивости уровней динамического ряда числа пожаров в городе за последние годы и выявление тенденции развития ряда
В качестве исходных данных для анализа используется представленный в табл. X.10 динамический ряд числа пожаров, произошедших в городе за последние шесть лет. Из табл. Х.10 следует выписать в соответствующие строки табл. 1.8 последовательность номеров уровней ряда t = 1, 2, ..., М (где М = 6 – общее число уровней), а также соответствующий каждому t–му уровню временной интервал Xt (год) и значение изучаемой характеристики Yt (число пожаров за год).
Производится расчет показателей, характеризующих изменчивость уровней динамического ряда Y1, Y2, Y3, ..., Yм. Предварительно необходимо зафиксировать так называемый базовый уровень ряда (Yбаз), который принимается в качестве базы для сравнения с текущим уровнем ряда (Yt). Обычно в качестве базового уровня принимают предшествующий уровень (Yt -1), либо начальный уровень (Y1), либо средний уровень ряда (Y).
К показателям, характеризующим изменчивость уровней динамического ряда относится абсолютный прирост, коэффициент (или темп) роста, коэффициент (или темп) прироста. Расчет этих показателей производится последовательно для каждого t-го уровня ряда (t = 1, 2, ...,М).
Абсолютный прирост (At) определяется как разность между рассматриваемым уровнем ряда (Yt) и некоторым уровнем, принятым за базу для сравнения (Yбаз):
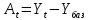(1.18)Значения абсолютного прироста At могут быть положительными (при Yt > Yбаз), отрицательными (при Yt < Yбаз), либо равными нулю (при Yt = Yбаз).
Коэффициент роста (Ht) определяется как отношение рассматриваемого уровня ряда (Yt) к уровню, принятому за базу для сравнения (Yбаз):
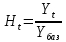(1.19)В зависимости от соотношений значений рассматриваемого и базового уровней значение коэффициента роста
Ht может оказаться меньше единицы (при Yt< Yбаз), равным единице (при Yt= Yбаз) или больше единицы (при Yt > Yбаз).
Коэффициент роста, выраженный в процентах, называется темпом роста. Коэффициент прироста (Bt) определяется как отношение абсолютного прироста (At) к уровню, принятому за базу для сравнения (Yбаз):
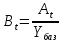(1.20)Значения Bt могут быть положительными, отрицательными, либо равными нулю в зависимости от значений абсолютного прироста. Коэффициент прироста, выраженный в процентах, называется темпом прироста. В качестве примера в табл. 1.8 представлены результаты расчета рассмотренных показателей изменчивости для интервального ряда динамики числа пожаров (Y) в городе за шесть лет (М = 6).
Таблица 1.8
Показатели изменчивости уровней ряда динамики числа пожаров в городе за шесть лет
| Показатели изменчивости уровней ряда динамики (цепные) | Значения показателей за год Xt | |||||
| 2005 г (t = 1) | 2006 г (t = 2) | 2007 г (t = 3) | 2008 г (t = 4) | 2009 г (t = 5) | 2010 г (t = 6) | |
| Число пожаров Yt за год Xt | 148 | 144 | 156 | 163 | 176 | 176 |
| Абсолютный прирост At = Yt - Yt-1 | - | -4 | +12 | +7 | +13 | 0 |
| Коэффициент роста Ht = Yt / Yt -1 | - | 0,973 | 1,083 | 1,045 | 1,080 | 1,000 |
| Темп роста (%) | - | 97,3 | 108,3 | 104,5 | 108,0 | 100,0 |
| Коэффициент прироста Bt = At / Yt -1 | - | -0,027 | 0,087 | 0,045 | 0,080 | 0 |
| Темп прироста (%) | - | -2,7 | 8,7 | 4,5 | 8,0 | 0 |
За базу для сравнения с текущим уровнем ряда Yt принимался предшествующий уровень ряда (Yбаз = Yt-1). Вычисляемые при таком условии показатели At, Ht и Bt (t = 1, 2, ..., М) называются цепными. Следует отметить, что при вычислении цепных показателей изменчивости, их значения, соответствующие уровню с номером t = 1, не подлежат расчету (в табл. 1.8 в соответствующем столбце проставлены прочерки), так как предшествующий ему уровень ряда (база для сравнения) отсутствует.
Для выявления тенденции развития временного ряда значение уровня временного ряда Yt, соответствующее интервалу времени (году) Xt (t =1, 2, 3,…, M) представляется в виде двух слагаемых
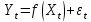(1.21)где f(Xt) – тренд, то есть функция, отражающая основную тенденцию развития динамического ряда; εt - случайная компонента динамического ряда, изменяющаяся со временем («шум»).
Произведем аналитическое выравнивание временного ряда, которое позволяет получить количественную модель, отражающую общую тенденцию развития ряда в виде функции времени
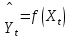(1.22)где
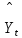– сглаженное значение уровня временного ряда, вычисленное с помощью модели для промежутка времени Xt (года) (t = 1, 2,…, M).Выбор вида функции (модели), приближенно описывающей тренд, является важным, но неформализованным этапом. На практике для этих целей используют имеющуюся априорную информацию, а также прибегают к анализу графического изображения уровней динамического ряда.
В качестве математической модели тренда выбираем как наиболее простую линейную функцию времени
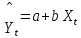(1.23)Неизвестные параметры a и b модели (1.23) оценивают по исходным значениям уровней динамического ряда Y1, Y2, Yз, ..., Yм и временных интервалов X1, X2, Xз, ..., Xм, руководствуясь стремлением обеспечить прохождение искомой линии тренда на графике как можно "ближе к точкам", отображающим уровни динамического ряда. Для этой цели используется метод наименьших квадратов (м.н.к.), в
основе которого лежит требование, чтобы сумма квадратов отклонений всех фактических значений Yt, от соответствующих расчетных значений
(i = 1, 2, ..., M) была минимальной, т.е.:
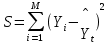
min (1.24)Для того, чтобы найти оценки параметров a и b линейной модели (1.23) с помощью м.н.к., заменим в выражении (1.24) значения
на соответствующую расчетную формулу (1.23) и получим: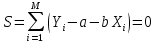
(1.25)Найдем выражения для частных производных величины S по a и по b, и приравняем их нулю, чтобы выполнялось требование (1.25):
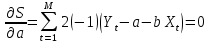(1.26)
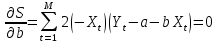(1.27)Подставляя в систему двух линейных уравнений (1.26) и (1.27) численные значения Yt и Xt (t = 1, 2,…, M), находим ее решение в виде оценок параметров a и b. Для этих целей путем преобразований получены формулы
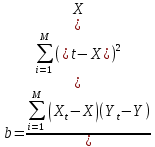(1.28)
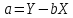(1.29)где Xи Y - средние арифметические значения для величин Xt и Yt (t = 1, 2, 3,…, M), которые вычисляются по формулам
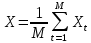(1.30)
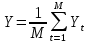(1.31)О качестве построенной модели можно ориентировочно судить по величине коэффициента детерминации D, показывающего, какую долю в общей вариации уровней динамического ряда удается объяснить с помощью модели тренда (величина D может находиться в пределах от 0 до 1). Для линейной модели (1.23) значение коэффициента детерминации D, вычисляется по формуле
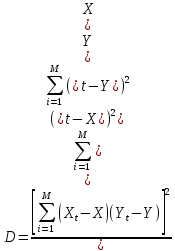(1.32)Для проведения расчетов по формулам (1.28) - (1.32) составляется табл. 1.9, в которой представлен пример вычислений по данным для города Н. В последней строке таблицы подсчитываются суммы данных по каждому столбцу, которые подставляются в расчетные формулы.
Таблица 1.9
Расчет статистических характеристик для оценки параметров линейной модели тренда для города
| t | Xt | Yt | Xt -X | Yt - Y | (Xt –X)2 | (Yt – Y)2 | (Xt –X)· (Yt – Y) | |
| 1 | 2005 | 148 | -2,5 | -12 | 6,25 | 144 | 30 | 143 |
| 2 | 2006 | 144 | -1,5 | -16 | 2,25 | 256 | 24 | 150 |
| 3 | 2007 | 156 | -0,5 | -4 | 0,25 | 16 | 2 | 157 |
| 4 | 2008 | 163 | 0,5 | 3 | 0,25 | 9 | 1,5 | 164 |
| 5 | 2009 | 176 | 1,5 | 16 | 2,25 | 256 | 24 | 171 |
| 6 | 2010 | 176 | 2,5 | 16 | 6,25 | 256 | 40 | 178 |
| Сумма | 12045 | 963 | 0 | 0 | 17,5 | 937 | 121,5 | 963 |
Средние арифметические значения X и Y , вычисляемые по формулам (1.30) и (1.31), по данным для города оказались следующими:
X = 12045 / 6 = 2007,5; Y = 963 / 6 = 161.
Оценки параметров a и b функции тренда (1.23), вычисляемые по формулам (1.28) и (1.29), по данным для города оказались следующими:
b = 121,5 / 17,5 = 6,9; a = 161 – 6,9 ∙ 2007,5 = – 13691.
Значение коэффициента детерминации D