ВУЗ: Казахский национальный медицинский университет им. С.Д. Асфендиярова
Категория: Учебное пособие
Дисциплина: Медицина
Добавлен: 04.02.2019
Просмотров: 1592
Скачиваний: 8
Медициналық-биологиялық зерттеулерде бір топты екінші топпен салыстыру тәсілдерімен қатар бір мезгілде бірнеше таңдамаларды салыстыруды қажет ететін есептер жиі кездеседі. Бұл жағдайда топтардың орта мәндерін жұп-жұбымен (әр топты әрқайсысымен) салыстыру тиімсіз болуы мүмкін, себебі салыстыру санының көптігінің салдарынан туатын I текті қателіктің жоғары мәні нәтижелер қорытындысының дұрыс жасалмауына әкеліп соғар еді. Сондықтан, салыстырылып отырған барлық топтардың арасында айырмашылықтың бар-жоғын бірден анықтау үшін бір ортақ статистикалық критерий қолданамыз.
Дисперсиялық талдау(Analysis Of Variance - ANOVA)
Дисперсиялық талдауды ағылшын ғалымы, математик және генетик Рональд Фишер XX ғасырдың 20-жылдарында жасап ұсынған.
Дисперсиялық талдау – бұл екіден артық топтардың орта мәндерін салыстыру үшін, яғни бірнеше тәуелсіз топтардың бір бас жиынтыққа жататындығын немесе жатпайтындығын анықтау үшін қолданылатын талдау әдісі. Орта мәндердің арасындағы айырмашылықтарды анықтау үшін дисперсиялар қолданылады.
Дисперсиялық талдау бірнеше деңгейлермен сипатталатын факторлардың ықпалын оқып үйрену үшін қолданылады.
Дисперсиялық талдау негізіне зерттеліп отырған жиынтықтыңбарлық элементтерінің орта мәннен ауытқуын талдау жатады. Ауытқу өлшемі ретіндеауытқулардың орта квадраты – дисперсия алынады.
Айталық, бізде бірнеше қалыпты таралған және дисперсиялары бірдей К бас жиынтықтары бар және берілген α мәнділік деңгейі бойынша олардыңорта мәндерініңтеңдігі жөніндегі нөлдік жорамалды тексеру қажет болсын. Ол үшін әрбір бас жиынтықтан таңдама ала отырып, алынған К таңдама орта мәндер арасындағы айырмашылықтың мәнді немесе мәнді еместігін анықтау қажет.
Барлық К бас жиынтықтары бір – бірімен ұқсас, яғни олардың дисперсиялары ғана емес, орта мәндері де бірдей деп ойлауға болады. Алайда бас жиынтықтардың әрқайсысы тәжірибеге енетін бір немесе бірнеше сапалы факторлардың ықпалына ұшырайды және соның нәтижесінде орта мәндер өзгеруі мүмкін.
Мысалы, гипертониямен ауыратын аурулардың бірнешеуікездейсоқтүрде К топқа бөлінген және әр топқа дәрінің белгілі бір түрін қабылдау белгіленген. Нәтижесінде артериялық қысымның өзгеруі көрсеткішінің орта мәні бақылауға алынады. Бұлмысалда дәрі – бақыланатын көрсеткіштің шамасына ықпал ететін фактор, артериялық қысымның өзгеруініңкөрсеткіші – фактордың ықпалына «жауап». Көп жағдайда «жауапты» нәтижелік белгі деп те атайды. Дәрінің түрлері – фактордың деңгейлері.
Факторлық белгілер (фактор) – зерттелетін құбылысқа ықпал ететін белгілер.
Нәтижелікбелгілер (факторға жауап) – факторлық белгілердің ықпалы нәтижесінде өзгеретін белгілер.
Бір фактордың ықпалы тексерілетін дисперсиялық талдау бірфакторлы деп аталады (ANOVA). Екі немесе одан да көп факторлардың ықпалын зерттеу үшін көпфакторлы дисперсиялық талдау (MANOVA – Multivariate ANOVA)қолданылады.
Бірфакторлы дисперсиялық талдау
Топтар бір фактордың деңгейлері арқылы анықталады. Бас жиынтықтағы айнымалы әр топта қалыпты таралған және барлық топтардың дисперсиялары бірдей.
Айырмашылықтын шамасын бағалау үшін таңдама орта мәндердің шашылуын топ ішіндегі мәндердің шашылуымен салыстыру қажет.
Салыстырылатын топтар саны фактордың (тәуелсіз айнымалы)деңгейлеріне сәйкес анықталады. Мысалы:фактор - жыл мезгілі болса, онда оның деңгейлері – қыс, көктем, жаз, күз. Салыстыралатын топ саны – 4. Фактор – емдеу тәсілдерінің түрі болса, онда оның деңгейлері: стандартты әдіспен емдеу, жаңа емдеу түріжәне плацебо (бақылау тобы) болуы мүмкін.Салыстырылатын топ саны – 3.
Дисперсиялық талдау жүргізу үшін сапалық белгілер (жыныс, профессия) де, сандық белгілер де (иньекция саны,аурулар саны) қолданылады.
Таңдама деректерді әдетте кесте түрінде бейнелейді, К деңгейдентұратын А факторы үшін кестенің түрі төмендегідей болады:
11-кесте
|
Сынау нөмірі |
А факторының деңгейлері |
||||
|
А1 |
А2 |
... |
Ак |
||
|
1 2 ... nj |
x11 x21 ...
|
x12 x22 ...
|
... ... ... ... |
x1k x2k ...
|
|
|
Топтық
орта мән |
|
|
... |
|
|
Келтірілген кестеде таңдамалар (бақылау топтары) фактор деңгейлеріне сәйкес және баған түрінде орналасқан. Таңдаманың әрбір элементіндегі бірінші индекс –таңдамадағы элементтің нөмірін, ал екінші индекс – топ нөмірін көрсетеді.
Топтық орта мән – әр топтағы элементтердің орта арифметикалық мәні:
![]()
nj саны j – ші таңдаманың көлемі, бақылаудың жалпы саны n = n1+n2+…+nk.
Жалпы алғанда, njсаны әртүрлі, алайда біз барлық таңдамалар көлемі тең болған жағдайды қарастырумен шектелеміз.
Дисперсиялық талдаудың негізгі идеясы таңдама дисперсияны екі компонентке (құрамдас бөлікке) бөлуге негізделген, олардың біреуі орта мәндердің өзгергіштігінефактордың ықпал етуіне сәйкес келеді (факторлық дисперсия), ал екіншісі кездейсоқ себептерден туған және ортамәндердің өзгергіштігінеықпал етпейтін дисперсия (қалдық дисперсия).
Топаралық дисперсия - фактордың таңдама орта мәндердің өзгергіштігіне ықпал етуінен туған дисперсия, оны факторлық дисперсия деп атайды және MSфактор (Mean Sqare) арқылы белгілейді.
Топішілік дисперсия – кездейсоқсебептерден туған және орта мәндердің өзгергіштігіне ықпал етпейтін дисперсия, оны қалдық дисперсия деп атайды және MSқалдық арқылы белгілейді.
Топтық орта мәндердің теңдігі жөніндегі нөлдік жорамалда топаралықдисперсия топішілік дисперсияға ұқсас. Егер салыстырылып отырған топтар арасында айырмашылық бар болса, онда топаралық дисперсия топішілік дисперсиядан үлкен болады. Фишер критерийі осы екі дисперсияның қатынасына негізделген.
ANOVA үшін Фишер критерийініңF статистикасы топаралық дисперсияның топішілік дисперсияға қатынасы арқылы анықталады.
![]()
F статистикасы (к- 1) және (n-к) еркіндік дәрежелеріне сәйкес келетін Фишер таралуына бағынады.
Факторлық дисперсия:
![]()
формуласы арқылы есептеледі.
Мұндағы
![]() – k орта мәндерден тұратын таңдаманың
(
– k орта мәндерден тұратын таңдаманың
(![]() таңдама
дисперсиясы.
таңдама
дисперсиясы.
![]()
![]()
Қалдық дисперсияны есептеу формуласы
![]()
мұндағы
![]() -
i-ші таңдаманың дисперсиясы
-
i-ші таңдаманың дисперсиясы
![]()
![]() үшін еркіндік дәржесінің саны (к
– 1),
мұндағы к-топтар
саны.
үшін еркіндік дәржесінің саны (к
– 1),
мұндағы к-топтар
саны.
![]() үшін еркіндік дәрежесінің саны к·(r-
1),
мұндағы r-әр
топтағы мәндер саны, к
- топтар саны,
үшін еркіндік дәрежесінің саны к·(r-
1),
мұндағы r-әр
топтағы мәндер саны, к
- топтар саны,
Факторлық дисперсия- топтық орта мәндердің шашырауын сипаттайды
Қалдық дисперсия– топтардың ішіндегі шашырауды сипаттайды.
Дисперсиялық талдауды жүргізу әдісі
К
тәуелсіз таңдамалар бар болсын және
олардың әрқайсысы жеке топты анықтайды.
Таңдамалар көлемдері - nі,
орта мәндер ![]() және орта квадраттық ауытқулар. Si
(i= 1,2,…,k) болсын.
және орта квадраттық ауытқулар. Si
(i= 1,2,…,k) болсын.
Таңдамалардың жалпы көлемі:n = n1+n2+…+nk
-
Нөлдік және балама жорамалдарды анықтаймыз:
Н0:
Бас жиынтықтың барлық топтық орта
мәндерітең:![]()
Н1: Бас жиынтықтың барлық топтық орта мәндері тең емес (ең болмағанда бір топтық ортаныңбасқалардан айырмашылығы бар).
-
Қажетті деректерді K таңдамалардан алу.
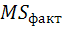 мен
мен 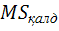 есептеу,
егер
есептеу,
егер 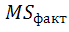 <
<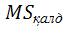 болса,онда
Н0
қабылданады,егер
болса,онда
Н0
қабылданады,егер 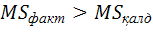 болса, онда Fкритерийін
есептейміз.
болса, онда Fкритерийін
есептейміз. -
Критерий статистикасын есептеу:Fбақ
-
α мәнділік деңгейіне сәйкес (α = 0,05 немесе α= 0,01) Фишер таралуының сыни мәнін арнайы кестеден табу.
-
F критерийінің статистикасын сыни нүктемен салыстыру
-
Н0 жорамалға қатысты шешім қабылдау: Егер Fбақ< Fсыни болса, онда берілген мәнділік деңгейінде нөлдік жорамал қабылданады.
Егер Fбақ> Fсыни болса, онда нөлдік жорамал жоққа шығарылады
және фактордыңықпалы маңызды болып табылады.
Дисперсиялық талдауды қолдануға қойылатын шарттар:
-
Әрбір таңдама басқа таңдамалардан тәуелсіз.
-
Әрбір таңдама зерттелетінбас жиынтықтан кездейсоқ түрде алынған.
-
Бас жиынтық қалыпты таралған.
-
Топтардың бас дисперсиялары бірдей.
Ескерту:Бұл талаптарды орындау аса маңызды. Сондықтандисперсиялықталдауды жүргізбес бұрын алдымен барлық салыстырылатын топтардың таралуын қалыптылыққа тексеру және осы топтардағыдисперсиялардың теңдігін тексеру қажет.
Бұл шарттардың ең болмағанда біреуі бұзылған жағдайда дисперсиялық талдауды қолдануға болмайды. Мұндай жағдайда бір факторлы ANOVA-ның параметрлік емес аналогы Крускал – Уоллис критерийін қолдану қажет.
Кочреннің қалыпты таралған бірнеше бас жиынтықтардың дисперсияларын салыстыру критерийі
Қалыпты таралған бірнеше бас жиынтықтардың дисперсияларының теңдігі (немесе дисперсиялардың біртектілігі) жөніндегі нөлдік жорамалды тексеру үшін Кочрен критерийі қолданылады:
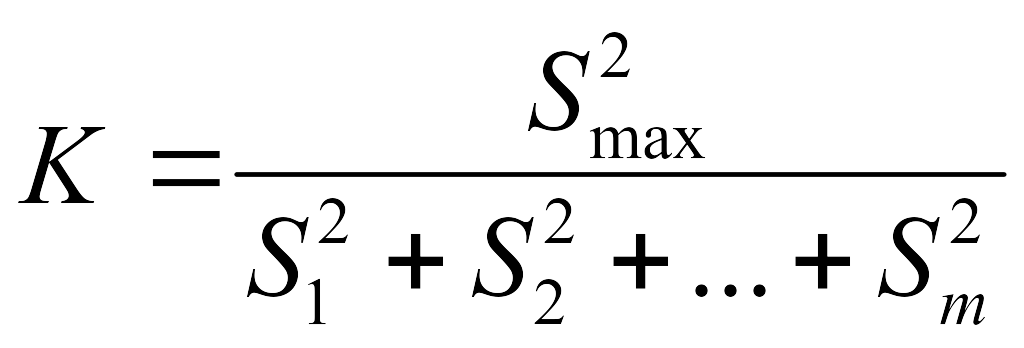
Мұндағы:
![]() –таңдама
дисперсиялардың ішіндегі мәні ең үлкен
дисперсия;
–таңдама
дисперсиялардың ішіндегі мәні ең үлкен
дисперсия;
![]() –m-ші
таңдаманың дисперсиясы;
–m-ші
таңдаманың дисперсиясы;
m–таңдамалар
саны (![]() ).
).
Алынған деректер бойынша Кбақ есептейміз және α (α=0,05 және α=0,01) мәнділік деңгейіне, df=n–1 еркіндік дәрежесінің санына, мұндағы n – таңдама көлемі, m-ге сәйкес Кочрен критерийінің сыни нүктелері кестесінен сыни нүктені табамыз (3-қосымша,3.8 -кесте).
Егер Кбақ<Ксыни болса, онда нөлдік жорамал қабылданады.
ЕгерКбақ>Ксыни болса, онда қарастырылып отырған бас жиынтықтардың дисперсиялары әртүрлі деген қорытынды жасалынады.
Мысал.Шылым шегудің тыныс алу жолдары ауруларына ықпалы.
Ересек тұрғындар арасында белгілі бір жас мөлшерлері бойынша тыныс алу жолдары ауруларымен ауырғандар саны екі жыл бойы бақыланды. Зерттеу мақсаты – шылым шегудің тыныс алу жолдары ауруларына ықпалын статистикалық дәлелдеу (тексеру). Әрқайсысы 4 адамнан тұратын 3 топ кездейсоқ түрде таңдалынып алынды, олардың: 1-тобына – шылым шекпейтіндер; 2-тобына - шылым шегу өтілдері5 жылға дейінгілер; 3-тобына – шылым шегу өтілдері 5 жылдан жоғарғылар жатқызылды.
Сонымен, зерттелетін фактор А – шылым шегу, фактор деңгейлері А1,А2,А3- шылым шегу өтілдері. Шылым шегу факторына жауап – тыныс алу жолдары ауруларының саны. Бақылау нәтижесінде аурулар санының 12 мәні алынды.
А1 тобында:
1-ші адам – 1 рет,
2-ші адам – 0 рет(ауырған жоқ),
3-ші адам – 1 рет,
4-ші адам – 2 рет ауырған.
А2 тобында:
1-ші адам – 3 рет,
2-ші адам – 2рет,
3-ші адам – 2 рет,
4-ші адам – 1рет ауырған, сол сияқты
А3 тобында:
1-ші адам – 3 рет,
2-ші адам – 4 рет,
3-ші адам – 5 рет,
4-ші адам –3 рет ауырған.
Таңдама қалыпты таралған бас жиынтықтан алынды деп ұйғарайық.
Дисперсиялық талдауды қолданбас бұрын Кочрен критерийі бойынша топтардағы таңдама дисперсиялардың теңдігіне көз жеткіземіз.
Кочрен критерийін қолданып дисперсиялардың теңдігін тексереміз.
-
Нөлдік және балама жорамаларды анықтау:
Н0:
![]()
Н1:
![]()
-
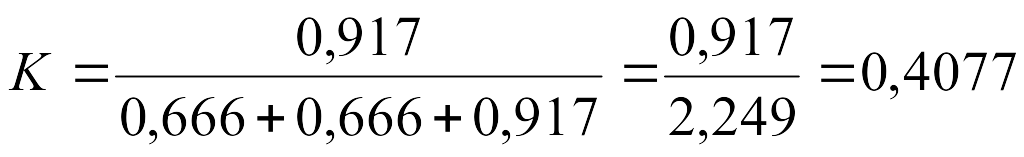 (13-кестеге
қараңыз)
(13-кестеге
қараңыз) -
α=0,05 болғанда сыни нүктені табамыз (3-қосымша, 3.8- кесте)Ксыни =Kα,df.m=K0,05;3;3=0,7977
Кбақ<Ксыниболғандықтан (0,4077<0,7977) α=0,05 деңгейінде дисперсиялардың теңдігі жөніндегі нөлдік жорамал қабылданады.
Демек, салыстырылып отырған бас жиынтықтардың дисперсиялары біртекті болғандықтан Фишердің критерийін қолданамыз.
Деректерді дисперсиялық талдау кестесіне енгіземіз:
12-кесте
|
Сынаулар нөмірі |
А |
||
|
А1 |
А2 |
А3 |
|
|
1 2 3 4 |
1 0 1 2 |
3 2 2 1 |
3 4 5 3 |
-
Нөлдік және балама жорамалдарды анықтаймыз:
Н0:
бас жиынтықтың үш тобындағы аурулар
санының орта мәндерінде айырмашылықтар
жоқ: ![]() ,
яғни шылым шегу тыныс алу жолдары
ауруларына маңызды ықпал етпейді.
,
яғни шылым шегу тыныс алу жолдары
ауруларына маңызды ықпал етпейді.
Н1:бас
жиынтықтың үш тобындағы аурулар санының
орта мәндерінде айырмашылықтар бар:
![]() ,
яғни шылым шегу тыныс алу жолдары
ауруларына маңызды ықпал етеді.
,
яғни шылым шегу тыныс алу жолдары
ауруларына маңызды ықпал етеді.
-
MS есептеу үшін таңдама деректерін дисперсиялық талдау кестесіне енгіземіз:
13-кесте
|
Сынаулар нөмірі |
Фактордың деңгейі |
||
|
А1 |
А2 |
А3 |
|
|
1 2 3 4 |
1 0 1 2 |
3 2 2 1 |
3 4 5 3 |
|
Сынаулар нөмірі |
Фактордың деңгейі |
||
|
А1 |
А2 |
А3 |
|
|
S2j |
-1,25 1,5625 S21=0,666 |
-0,25 0,0625 S22= 0,666 |
1,5 2,25 S23 =0,917 |
![]()
S21=![]()
S22=![]()
S23=![]()
Кестеде F-критерийін есептеу үшін қажетті барлық деректер бар.Алдымен факторлық және қалдық дисперсияларды табамыз.
![]() =r*
S2
=r*
S2![]() =
=![]()
![]() =4*
=4*![]()
![]() S21+S22+S23)=
S21+S22+S23)=![]()
![]()
![]()
![]() болғандықтан
F-критерийін есептейміз.
болғандықтан
F-критерийін есептейміз.
3.Fбақ=
![]()
4.Fсыни(0,05;2;9)=4,26 (3-қосымша, 3.7- кесте)
Fсыни(0,01;2;9)=8,02
5.α=0,05
және α=0,01
болғанда да Fбақ![]() Fсыни,яғнибақылау
мәні сыни аймаққа түсті.
Fсыни,яғнибақылау
мәні сыни аймаққа түсті.
6.Топтық орта мәндердің теңдігі жөніндегі H0 жорамалын жоққа шығарамыз.
7. Есептеу нәтижелерін дисперсиялық талдау кестесіне енгіземіз.
14-кесте
|
Дисперсиялар |
Еркіндік дәрежеле-рінің саны |
Орта квадрат MS |
|
|
|
Топаралық (фактор А) |
k-1=2 |
MSфакт=7,75 |
= |
|
|
Топішілік (қалдық) |
k(r-1)=9 |
MSкалд=0,75 |
|
|
|
Жалпы |
k· r -1=11 |
MSжалпы |
|
|