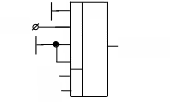
Приведем условные графические обозначения (УГО) некоторых мультиплексоров:


2x


2x1

4x1


Как выглядят УГО мультиплексоров 8x1 и 16x1?

Любую булеву функцию можно реализовать с помощью мультиплексора. Для этого аргументы функции подают на адресные входы мультиплексора, а значения функции на соответствующие селектируемые входы.

Пример. Реализовать на мультиплексоре функцию:

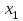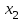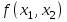0	0	0
0	1	1
1	0	0
1	1	0

Не следует думать, что число аргументов реализуемой функции должно быть обязательно равно числу адресных входов мультиплексора. Число аргументов может быть большим, но логика формирования селектируемых сигналов обычно усложняется.

Пример: Реализовать на мультиплексоре 4x1 функцию:

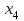	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
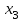	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
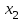	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
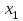	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
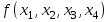	0	0	0	1	0	1	1	1	0	1	0	1	0	0	0	0

---

Подключим к адресным входам мультиплексора 4x1 два аргумента, например и . При таком подключении сигнал на адресном входе совпадает с , а на входе с . Поскольку на первых четырех наборах 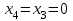, то сигнал на выходе мультиплексора совпадает с сигналом на шине . Нижняя строчка таблицы на наборах 0, 1, 2, 3 показывает какой сигнал должен формироваться на шине . Эти сигнал не постоянен, следовательно он зависит от еще не учтенных аргументов и : 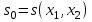. Легко увидеть, что логика формирования сигнала .

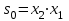Рассуждая аналогично можно найти логику формирования сигналов на остальных селектируемых шинах: , , .

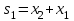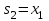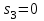№ набора	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
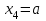	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
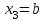	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
	0	0	0	1	0	1	1	1	0	1	0	1	0	0	0	0

---

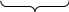
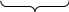
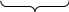
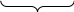
Сигнал на Сигнал на Сигнал на Сигнал на





Сложность логики, формирующей сигналы на селектируемых входах, зависит от того, какие аргументы подключены к адресным входам. Оптимальную схему можно получить, выполнив синтез для всех возможных комбинаций адресных сигналов.

Если брать мультиплексор с числом адресных входов на единицу меньше, чем число аргументов функции, то для реализации функции потребуется мультиплексор и, возможно, один инвертор.

Пример: Реализовать функцию заданную таблично

№ набора	0	1	2	3	4	5	6	7
	0	0	0	0	1	1	1	1
	0	0	1	1	0	0	1	1
	0	1	0	1	0	1	0	1
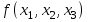	1	0	0	1	1	1	0	0

---

Заметим, что если бы на нулевом наборе функция была бы равна нулю, а на первом наборе – равна единице, инвертор не понадобился бы.

---

Функциональная полнота систем булевых функций.
Одно из основных требований к системе логических элементов, состоит в том, чтобы из элементов этой системы можно было построить любую логическую схему. Техническая задача отыскания такой системы элементов сводится к математической задаче определения набора функций, из которых методом суперпозиции можно получить любую функцию.
Система булевых функций называется функционально полной, если произвольную булеву функцию можно представить суперпозицией функций этой системы.

Для решения задачи были выделены пять классов булевых функций:

- сохраняющие нуль – это функции равные нулю на нулевом наборе аргументов: ;

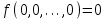- сохраняющие единицу – это функции равные единице на единичном наборе:

;

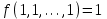- самодвойственные булевы функции на каждой паре противоположных наборов принимают противоположные значения: ;

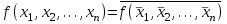- линейные булевы функции - это функции, которые можно представить линейным полиномом: ,

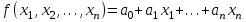где .

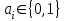Если значения каждого аргумента одного набора больше или равно значению того же аргумента второго набора, то говорят, что первый набор не меньше второго. Следует заметить, что не все наборы являются сравнимыми, например (1,0,1) и (0,1,0) не сравнимы.

- монотонной булевой функцией называют функцию, у которой при любом возрастании набора аргументов значения функции не убывают.

Известна теорема о функциональной полноте: для того чтобы система булевых функций была функционально полной, необходимо и достаточно, чтобы эта система включала:

- хотя бы одну функцию, не сохраняющую нуль;

- хотя бы одну функцию, не сохраняющую единицу;

- хотя бы одну нелинейную функцию;

-хотя бы одну немонотонную функцию;

-хотя бы одну несамодвойственную функцию.

В таблице показано, к каким классам относятся функции двух аргументов:

Функция	Сохраняет нуль	Сохраняет единицу	Самодвойст-венная	Монотонная	Линейная
0	x			x	x
	x	x		x
	x
	x	x	x	x	x
	x
	x	x	x	x	x
	x				x
	x	x		x
		x			x
			x		x
		x
			x		x
		x
1		x		x	x

---

Смотрите также файлы

• Реконструкция средней школы 18 в г. Белгороде.docx

• Вестник пнипу. Аэрокосмическая техника. 2014. 39 50.pdf

• Расчет параметров бвр.docx

• При проектировании фрагмента занятия следуйте логике методической разработки.docx

• Гормоны гипофиза у плода.docx