ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 90
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Итак, если на вход дешифратора подать аргументы булевой функции, то на
выходах дешифратора можно получить все конституенты единицы. Число входов дешифратора
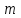связано с числом выходов 
соотношением 
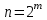. Дешифраторы с двумя, тремя, четырьмя и т.д. входами можно рассматривать как генераторы конституент единицы для функций 2, 3, 4, и т.д. аргументов. Суммируя конституенты единицы для наборов, где функция равна 1, мы получаем реализацию этой функции. Приведем условные графические обозначения ( УГО) дешифраторов с 2 и 3 входами:
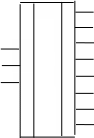
Пример: реализовать систему булевых функций на дешифраторе с прямыми выходами.
 |  |  |  |  | | | | | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | * |
| 0 | 1 | 0 | * | 0 | 1 | 1 | 0 | 1 | * |
| 0 | 1 | 1 | * | 0 | 1 | 1 | 1 | 0 | 0 |
Функции
и зависят от трех аргументов, следовательно, необходим дешифратор с тремя входами. Особенностью этих функций является то, что они заданы не на всех наборах. Такие функции называют не полностью определенными булевыми функциями. Наборы, на которых функция не определена, помечены символом *. Эти функции необходимо доопределить, т. е. приписать функциям нам этих наборах значения 0 или 1.Доопределение проводят таким образом, чтобы получить наиболее простую схему. Для данного примера выгодно доопределить эти наборы нулями.
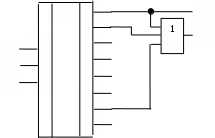
Существуют дешифраторы с инверсными выходами. Схема такого дешифратора имеет вид:
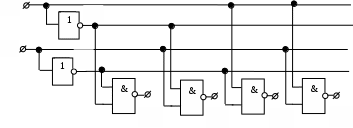
Запишем уравнения для этого дешифратора:
, 
, 
, 
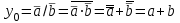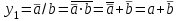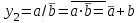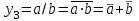. Построим таблицы истинности для этих уравнений:
| | |  |  |  |  Видно, что такой дешифратор формирует на своих выходах все конституенты нуля булевых функций двух аргументов:  ,  ,  ,  , ,.  |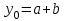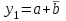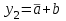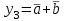
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
Условные графические обозначения дешифраторов с инверсными выходами отличаются от дешифраторов с прямыми выходами наличием значков инверсии на выходах:
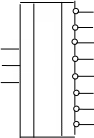входами: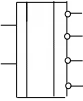
Такие дешифраторы являются генераторами конституент нуля и позволяют реализовывать булевы функции путем перемножения конституент нуля. Если реализовать функции из предыдущего примера на таких дешифраторах, то получим схему:
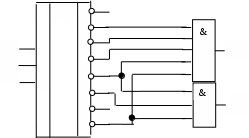
Мультиплексоры.
Проведем анализ еще одной простейшей схемы, которую называют
мультиплексором:
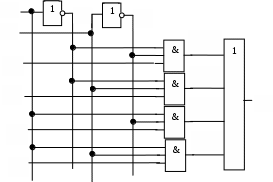
Запишем уравнение для выходного сигнала мультиплексора:
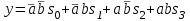. Функция зависит от шести аргументов, поэтому таблица истинности будет слишком громоздкой. Вычислим значения функции 
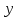задавая только значения и :| | |  |
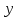| 0 | 0 |  |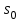
| 0 | 1 |  |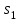
| 1 | 0 |  |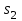
| 1 | 1 |  |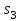
Входы
и мультиплексора называют адресными, а входы 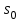, , 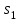, 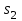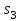-селектируемыми. Из таблицы видно, что мультиплексор подключает к своему выходу один из селектируемых входов
, номер которого определяется кодом на адресных шинах.
Число селектируемых входов равно
, где - число адресных входов.В литературе тип мультиплексора часто задают обозначением
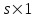, здесь 
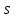- число селектируемых входов мультиплексора, которые коммутируются на 1 выход. Существуют мультиплексоры 2x1, 4x1, 8x1, 16x1, 32x1 и т.д. Мы рассмотрели мультиплексор 4x1. Принцип работы других мультиплексоров подобен работе мультиплексора 4x1. Например функционирование мультиплексора 8x1 можно пояснить аналогичной таблицей:| | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
 |  |  |  |  |  |  |  |  |
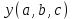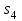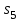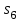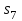Постройте самостоятельно подобные таблицы для мультиплексоров 2x1 и 16x1.