Файл: Отчет лабораторная работа 1 типовые звенья и их характеристики выполнил Студент гр. 5101 07 мая 2023 г. Проверил.docx

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ

УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра компьютерных систем в управлении и проектировании (КСУП)
ОТЧЕТ
Лабораторная работа № 1
ТИПОВЫЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ
Выполнил

Студент гр. 510-1

«07» мая 2023 г.
Проверил:

К.т.н., доцент

___________ А. Г.Карпов

«___» _____________ 2023 г.


Томск 2023

1 Введение

Целью данной работы является изучение моделей и характеристик основных типовых звеньев и ознакомление с моделирующей установкой РВЛ ТАУ.
2 Основные соотношения
Дифференциальное уравнение второго порядка имеет вид:



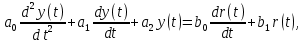
где y(t) – выход звена, а r(t) – вход звена.

Названия наиболее часто используемых звеньев и их параметры приведены в таблицы 2.1.
Таблица 2.1 – Наиболее часто используемые типовые звенья и их параметры

№	Название звена		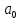		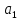		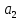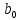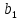Примечание
1	Безынерционное (усилительное)	0	0	1	0	110
2	Апериодическое 1-го порядка	0	0.1	1	0	110
3	Апериодическое 2-го порядка	0.0016	0.1	1	0	110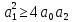
4	Колебательное	0.04	0.1	1	0	110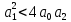
5	Идеальное интегрирующее	0	1	0	0	110
6	Интегрирующее с замедлением	0.1	1	0	0	110
7	Идеальное дифференцирующее	0	0	1	110	0
8	Дифференцирующее с замедлением	0	0.1	1	10	0

---

3 Ход работы

Дифференциальные уравнения для соответствующих звеньев:

1. 
   безынерционное звено: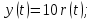
   
2. 
   апериодическое звено первого порядка: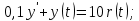
   
3. 
   апериодическое звено второго порядка:
   

4. 
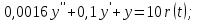
   колебательное звено: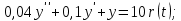
   
5. 
   идеальное интегрирующее: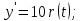
   
6. 
   интегрирующее звено с замедлением: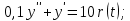
   
7. 
   идеальное дифференцирующее: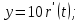
   
8. 
   дифференцирующее с замедлением звено: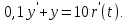
   

Согласно имеющемуся заданию, произведем расчет простейших звеньев.
3.1.Безынерционное (усилительное) звено

Произведем замену 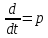, чтобы перейти к операторному уравнению, получим:

F(p) =10F1(p)

Передаточная функция:.
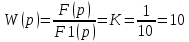
Весовая (импульсная переходная) функция:. h(t) = K·1(t) = 10·1(t)
На рис. 3.1 представлен график весовой функции. w(t) = h'(t) = 0



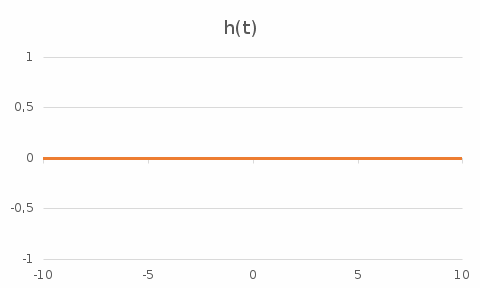
Рис. 3.1 – График весовой функции
На рис. 3.2 представлен график переходной характеристики.


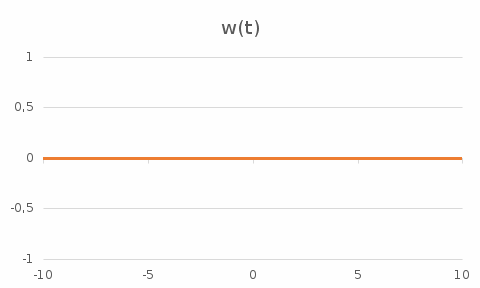
Рис. 3.2 – График переходной характеристики
Амплитудная частотная характеристика (АЧХ):

A() = W(j) = 10 .

На рисунке 3 представлен график АЧХ



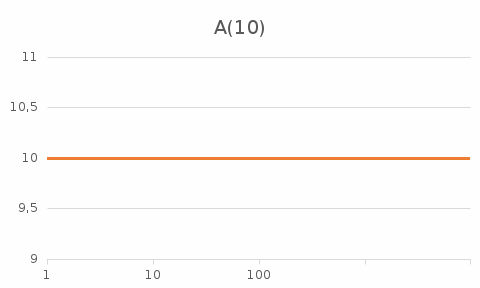
Рис. 3.3 – График AЧХ.

Фазовая частотная характеристика (ФЧХ):

Ф(ω) =arg(W(iω)) = 0

На рис. 3.3 представлен график ФЧХ.

---

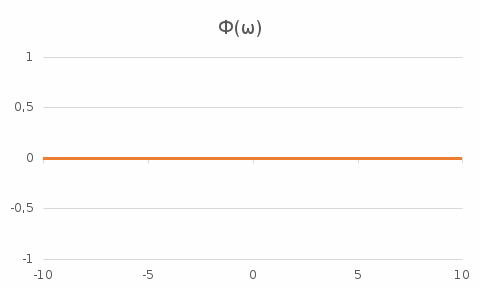
Рис. 3.4 – График ФЧХ
Логарифмическая амплитудная частотная характеристика (ЛАЧХ):

L(ω) = 20log A(ω) = 20log|W(iω)| = 10

На рис. 3.4 представлен график ЛАЧХ.



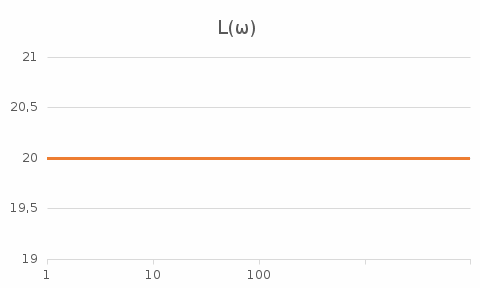
Рис. 3.5 – График ЛАЧХ
Амплитудно-фазовая частотная характеристика (АФЧХ):

P() =10 ; Q() = 0

На рис. 3.5 представлен график АФЧХ.



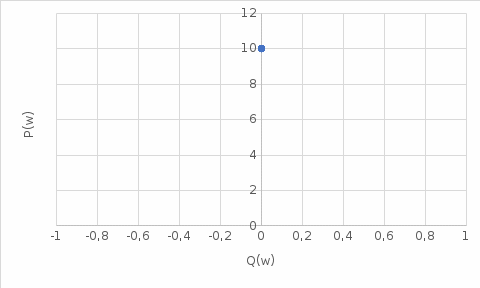
Рис. 3.6 – График АФЧХ
3.2. Апериодическое звено 1-го порядка

Произведем замену , чтобы перейти к операторному уравнению, получим:

(0.1p +1)F1(p) =10F(p).

Передаточная функция:



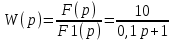
Переходная функция:



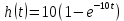
Весовая функция:



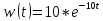
На рис. 3.6 представлена весовая функция.



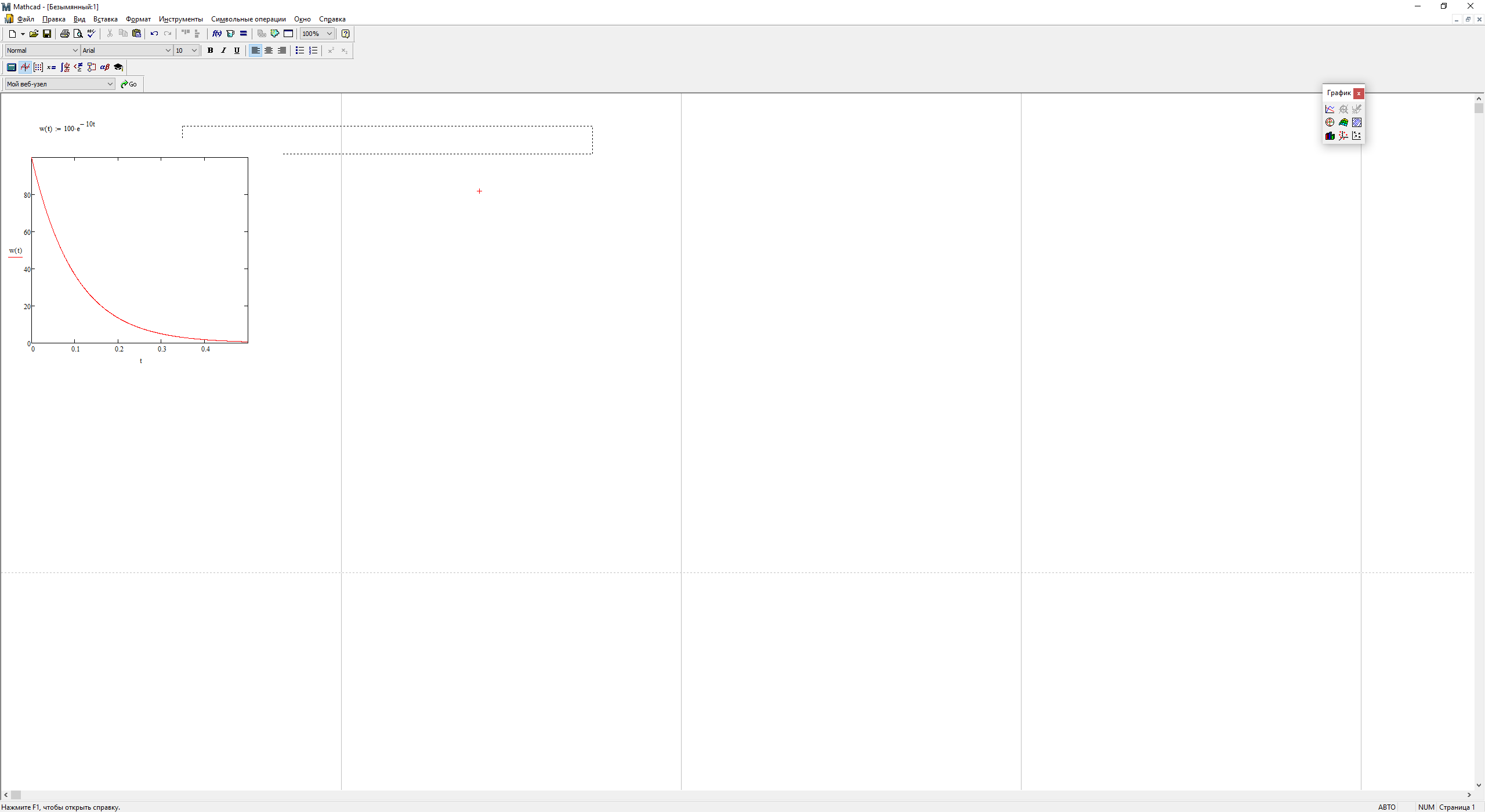
Рис. 3.7 – График весовой функции

На рис. 3.7 представлена переходная характеристика.



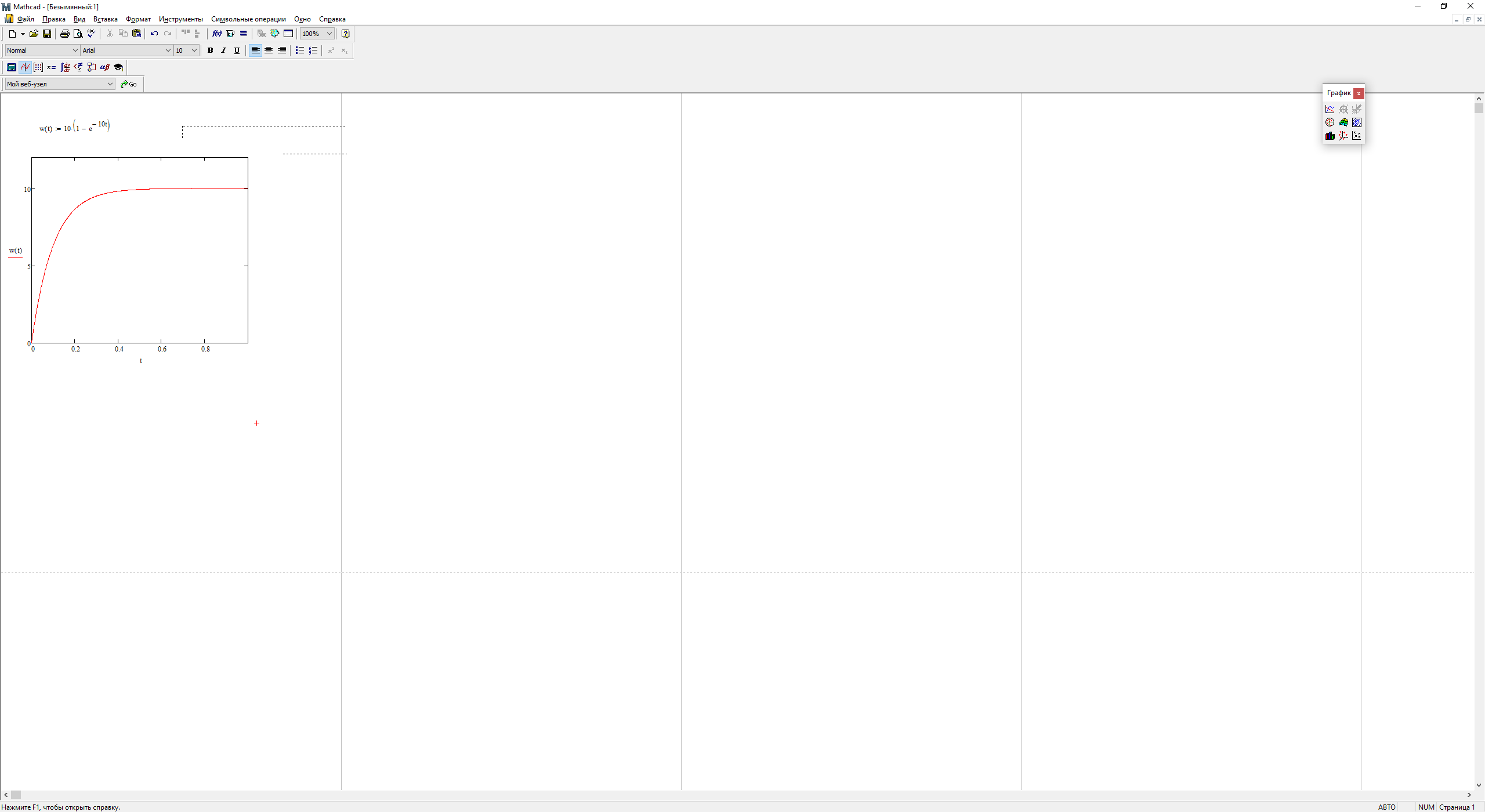
Рис. 3.8 – График переходной характеристики
Амплитудная частотная характеристика (АЧХ):



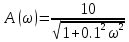
На рис. 3.8 представлен график АЧХ.



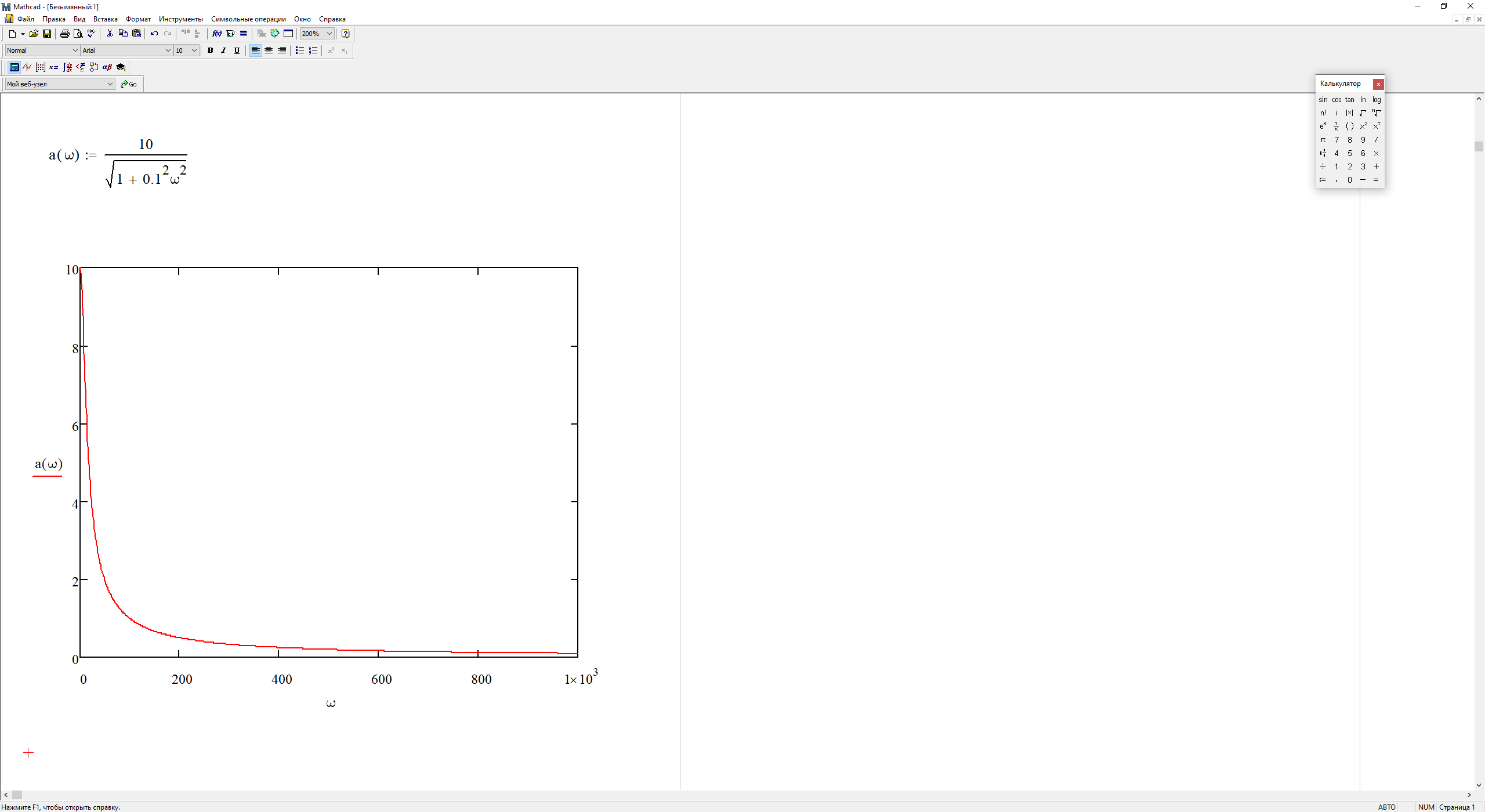
Рис. 3.9 – График АЧХ
Фазовая частотная характеристика (ФЧХ):

Ф (ω) = arg(W(iω)) = -arctg(0,1ω)

На рис. 3.9 представлен график ФЧХ.



Рис. 3.10 – График ФЧХ

Логарифмическая амплитудно-частотная характеристика (ЛАЧХ):



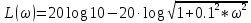
На рис. 3.10 представлен график ЛАЧХ.



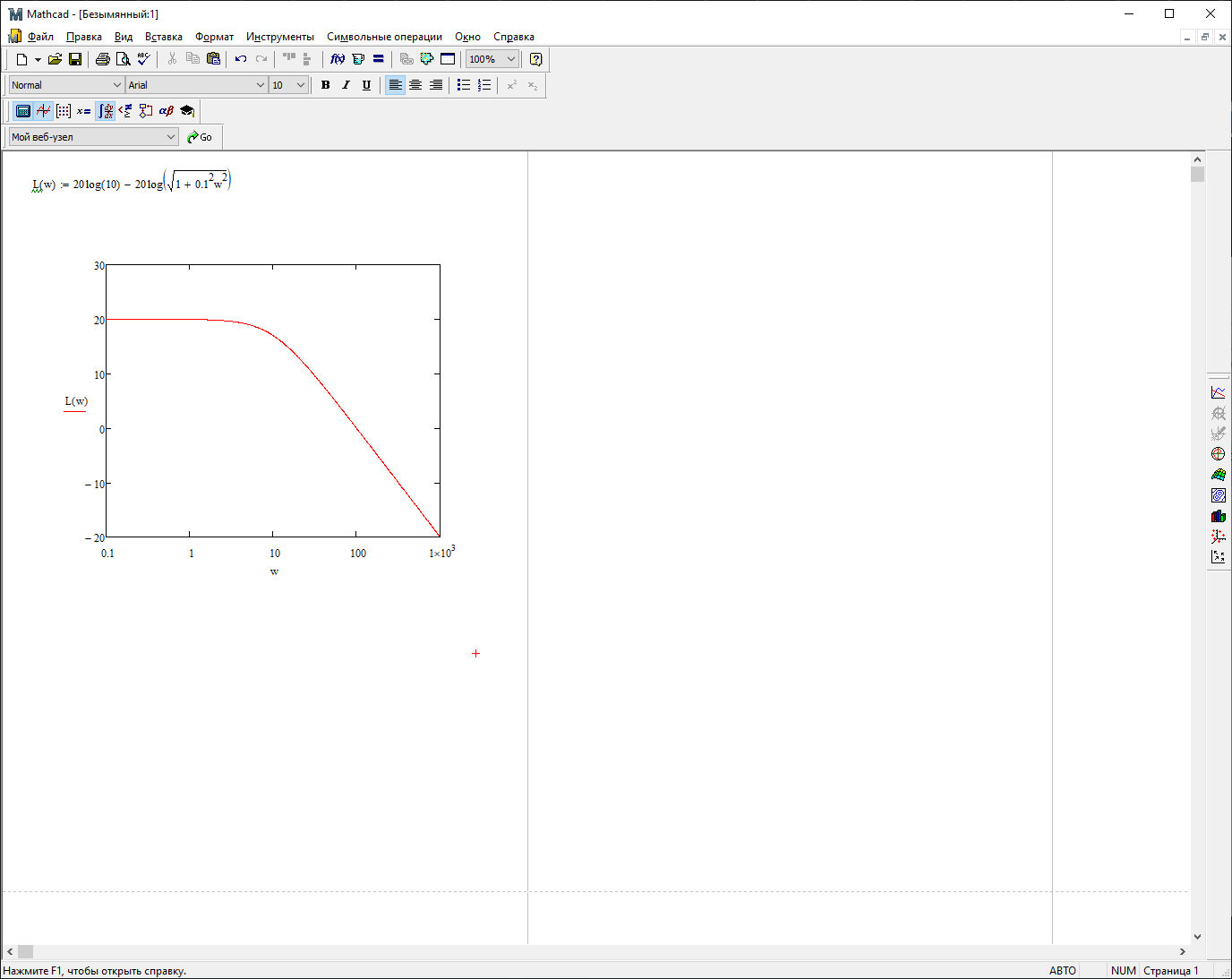
Рис. 3.11 – График ЛАЧХ
Амплитудно-фазовая частотная характеристика (АФЧХ):



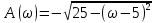
На рис. 3.11 представлен график АФЧХ.



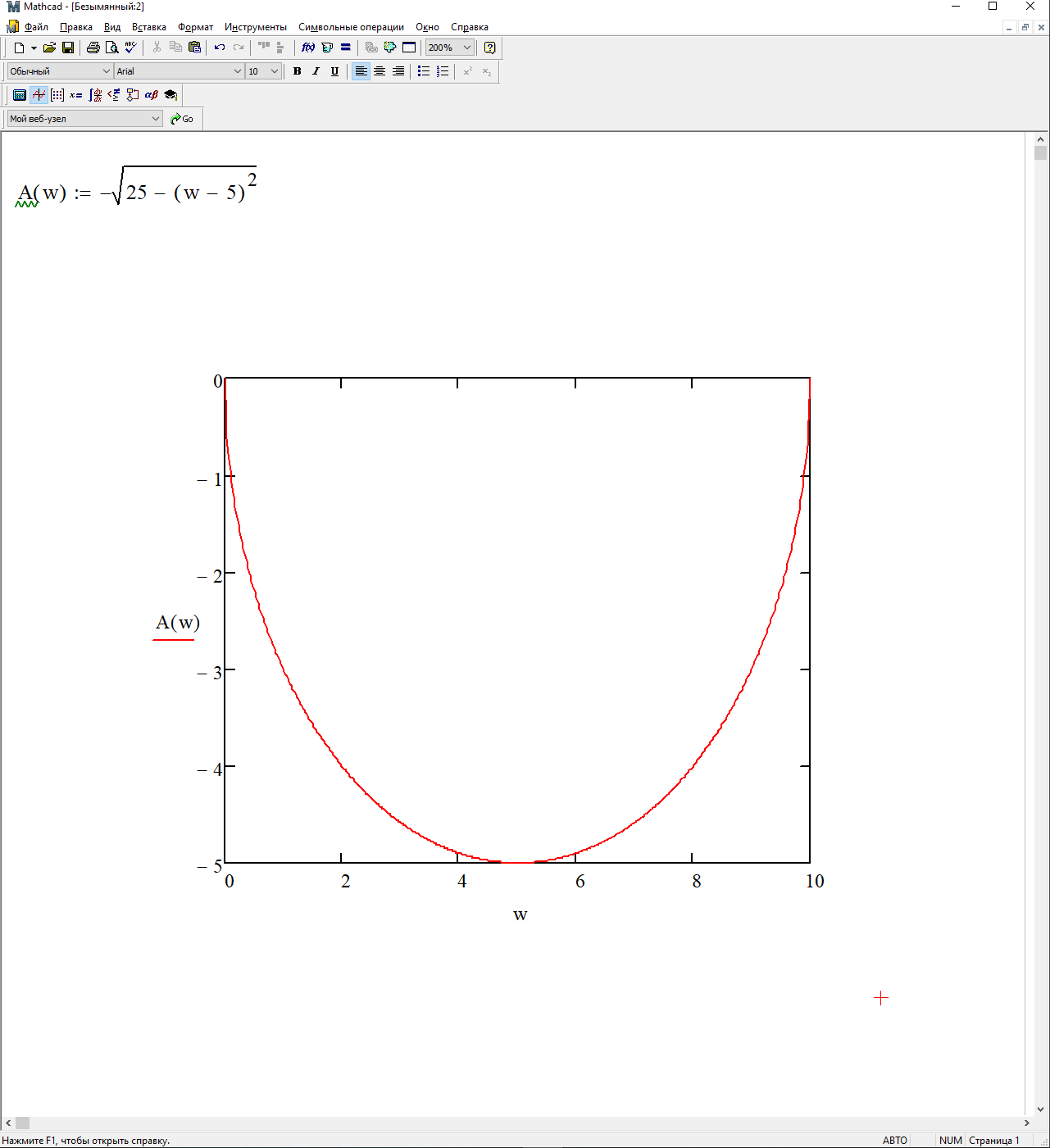
Рис. 3.12 – График АФЧХ
3.3. Апериодическое звено 2-го порядка (инерционное)

---

Произведем замену , чтобы перейти к операторному уравнению, получим:

(0.0016p²+0.1p+1)F1(p)=10F(p)

Передаточная функция:


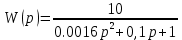
Весовая функция: W(t):





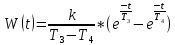
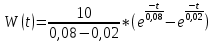
График весовой функции представлен на рисунке 3.12.
Переходная характеристика h(t):





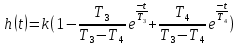
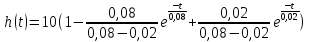
График переходной функции представлен на рисунке 3.13.



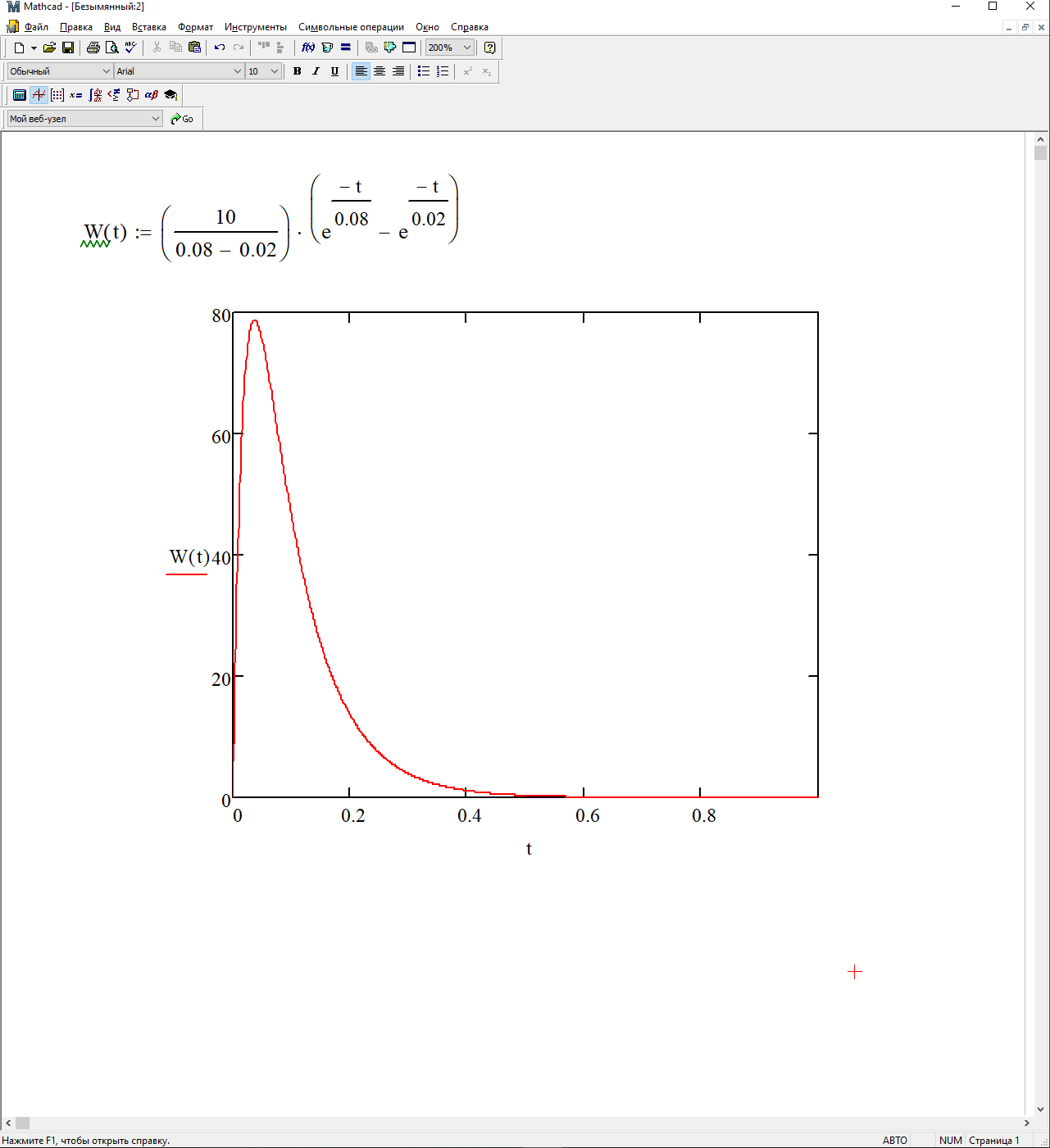
Рисунок 3.13 – График весовой функции


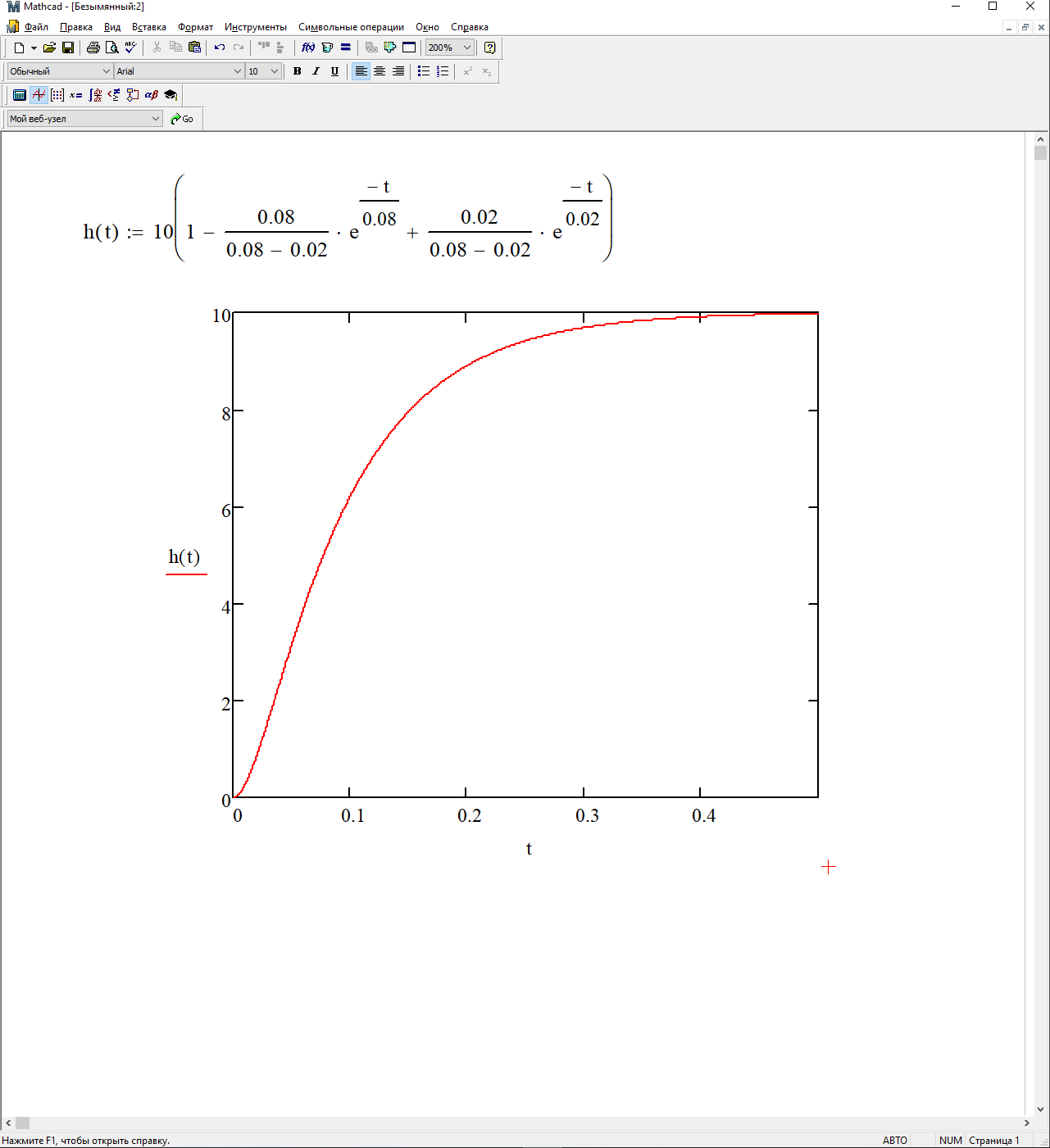
Рисунок 3.14 - График переходной функции

Амплитудная частотная характеристика (АЧХ):



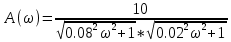
На рисунке 3.14 представлен график АЧХ.



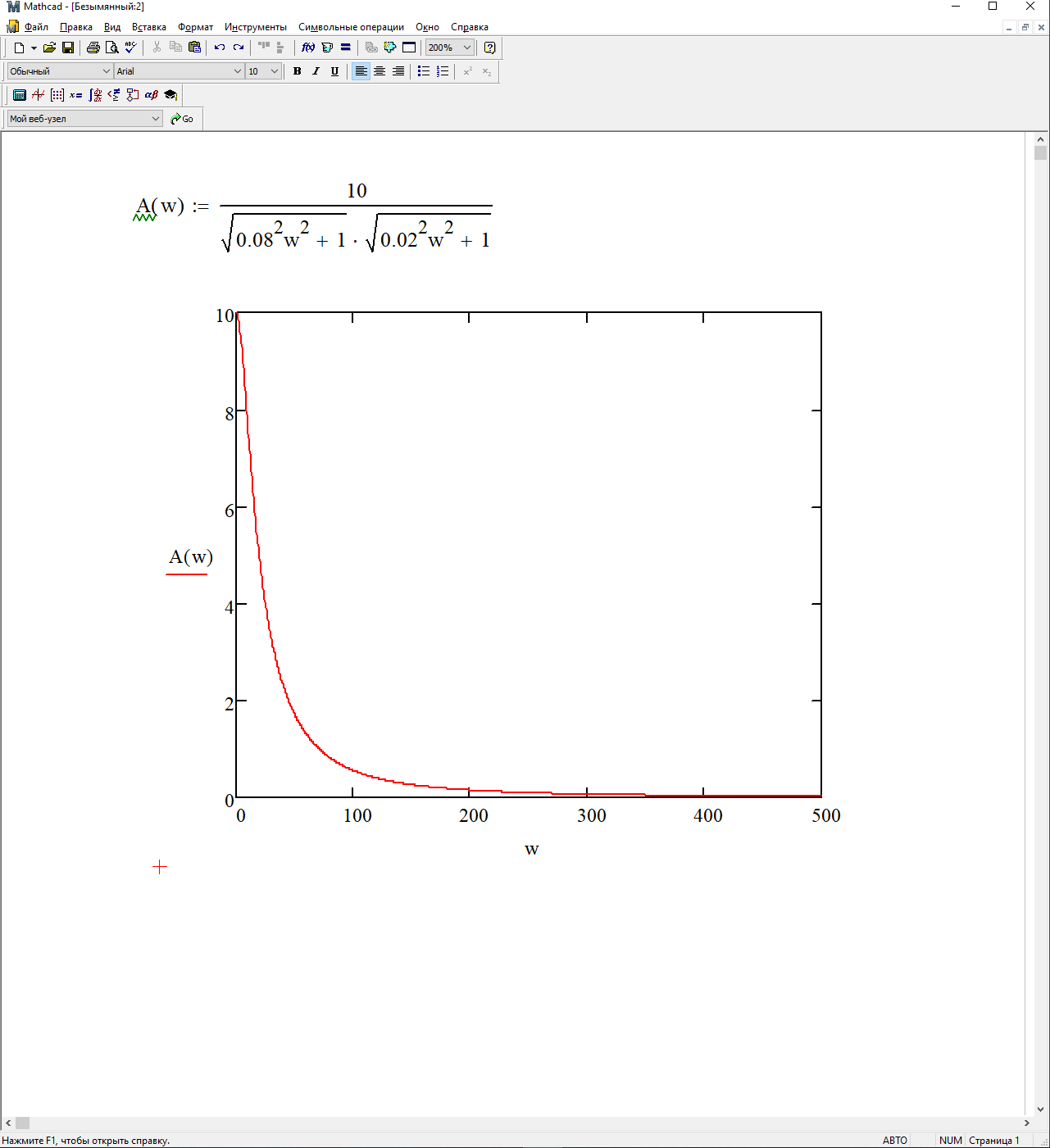
Рисунок 3.15 - график АЧХ.

Фазовая частотная характеристика (ФЧХ):
Ф(ω) = -arctg(0.08 ω)-arctg(0.02 ω)
На рис. 3.16 представлен график ФЧХ.


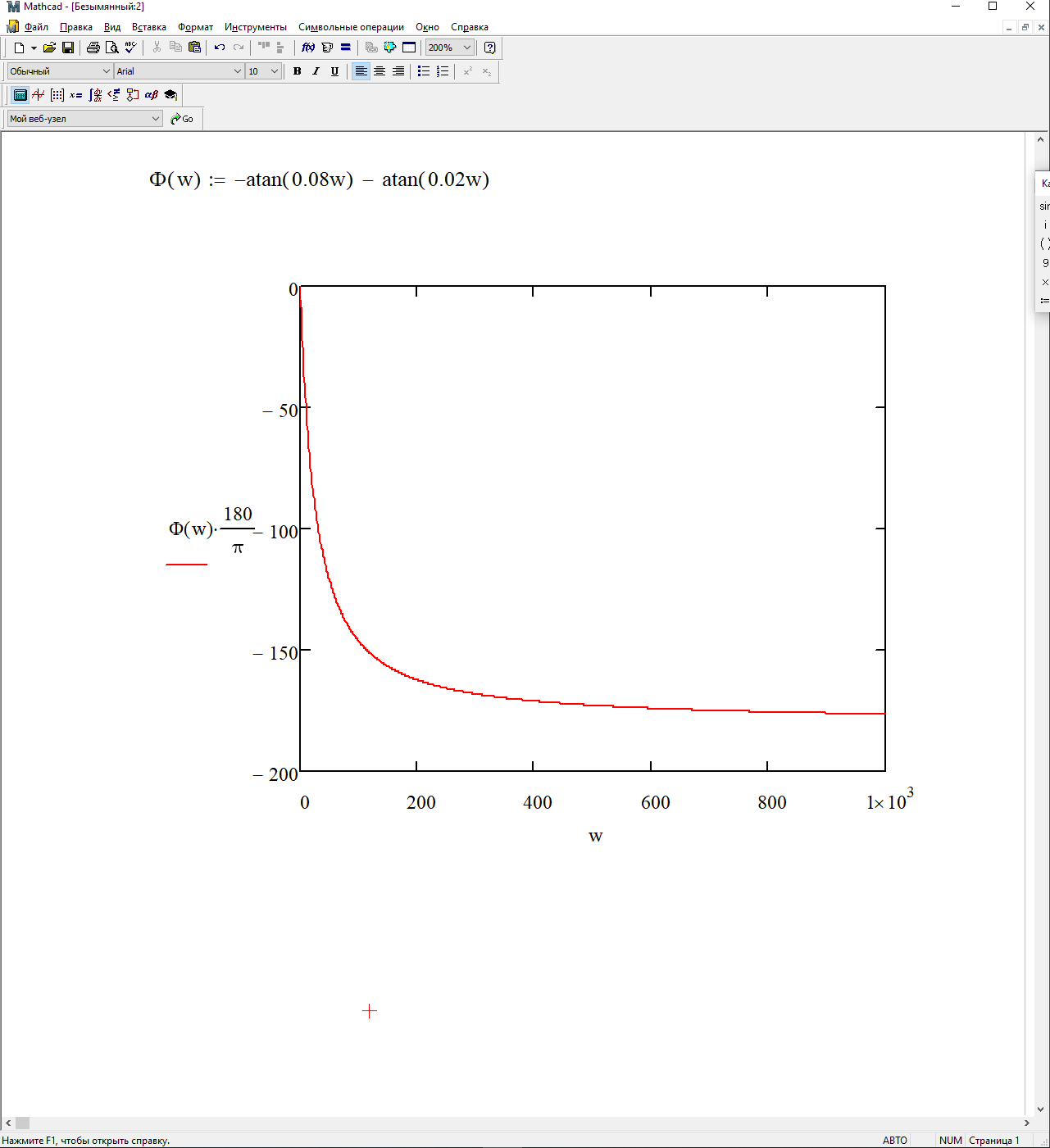
Рисунок 3.16 - график ФЧХ.

Логарифмическая амплитудно-частотная характеристика (ЛАЧХ):



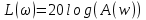
На рис. 3.16 представлен график ЛАЧХ.


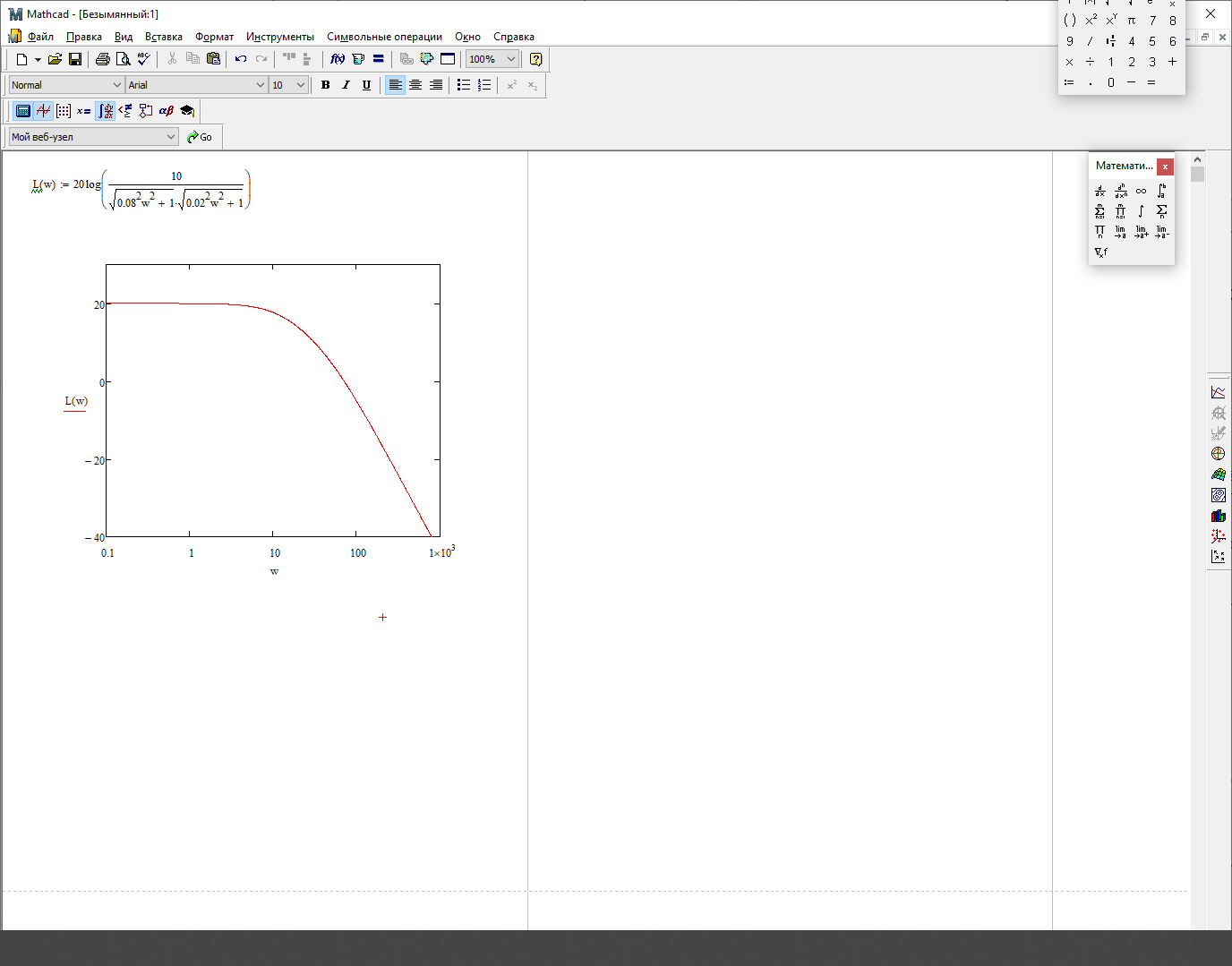
Рисунок 3.17 - график ЛАЧХ.
Амплитудно-фазовая частотная характеристика (АФЧХ):





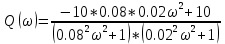
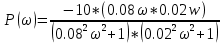
На рис. 3.18 представлен график ЛАЧХ.



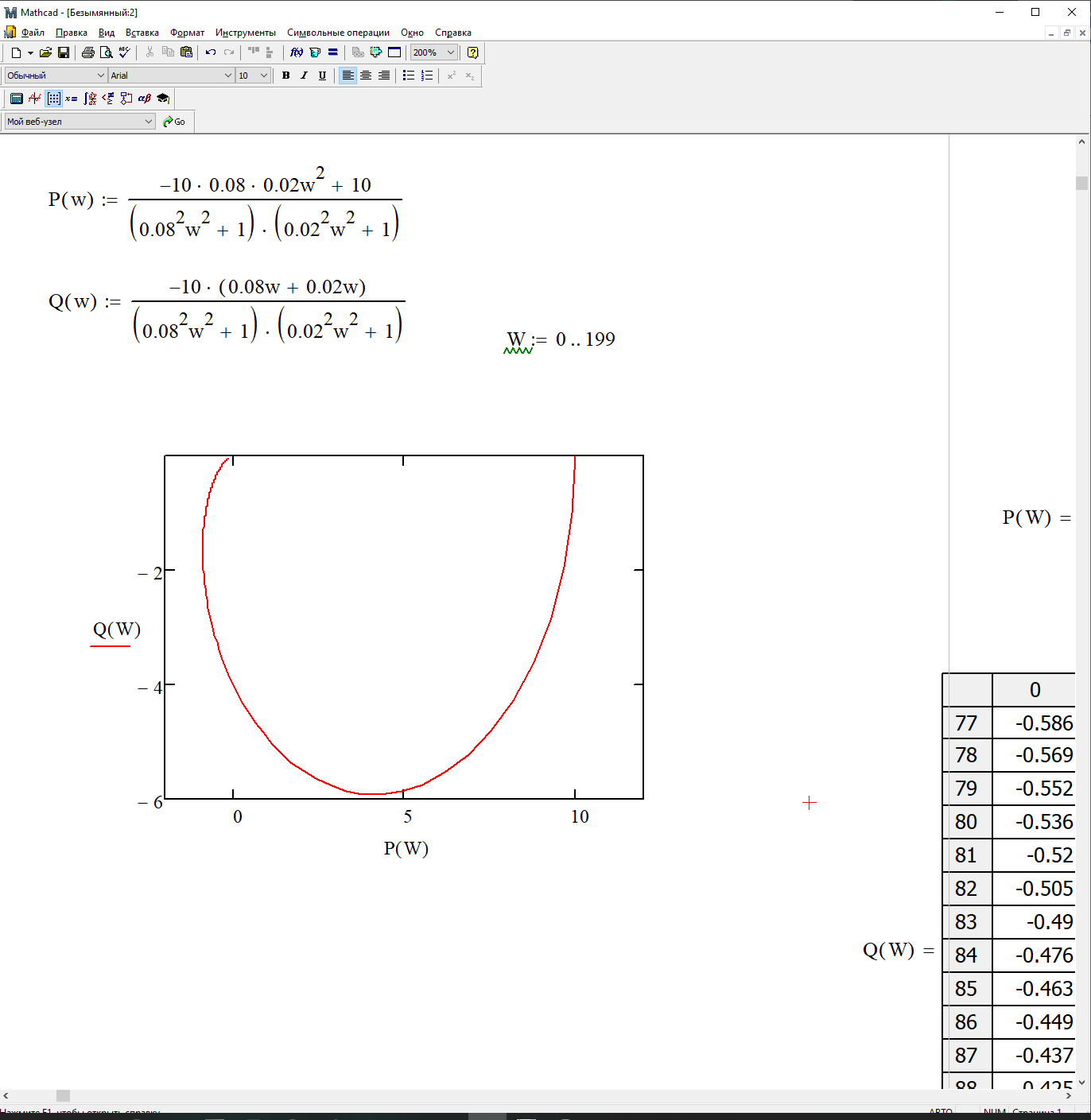
Рисунок 3.18 - график АФЧХ.
3.4. Колебательное звено

Произведем замену , чтобы перейти к операторному уравнению, получим:

(0.04p²+0.1p+1)*F1(p)=10F(p)

Передаточная функция:

---

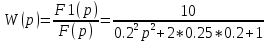
Весовая функция:



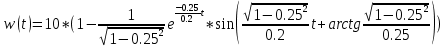
На рис. 3.19 представлен график весовой функции.


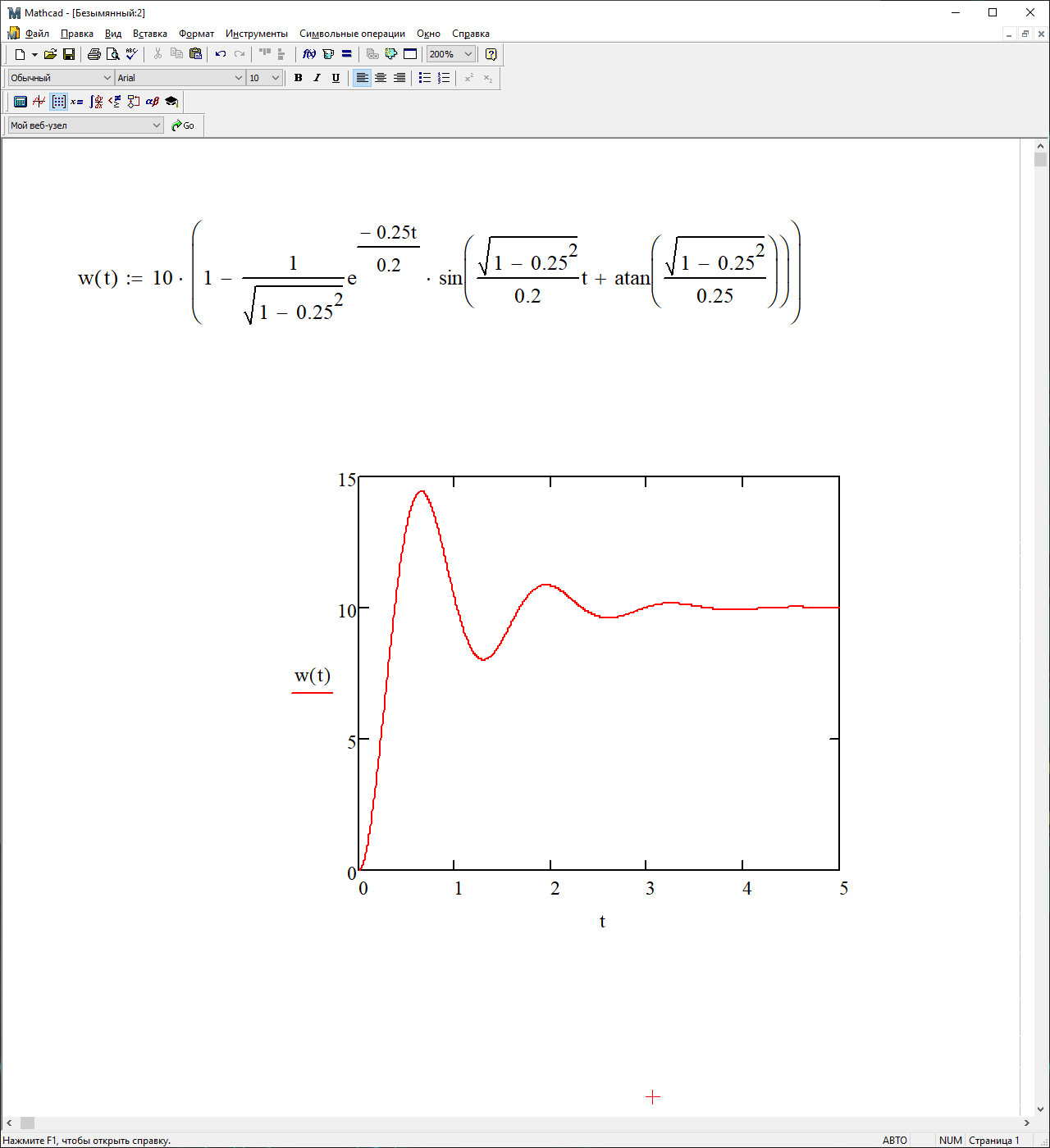
Рисунок 3.19 - график весовой функции.
Переходная функция:




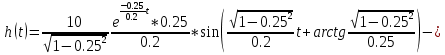
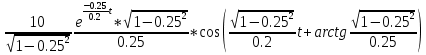
На рис. 3.20 представлен график переходной функции.


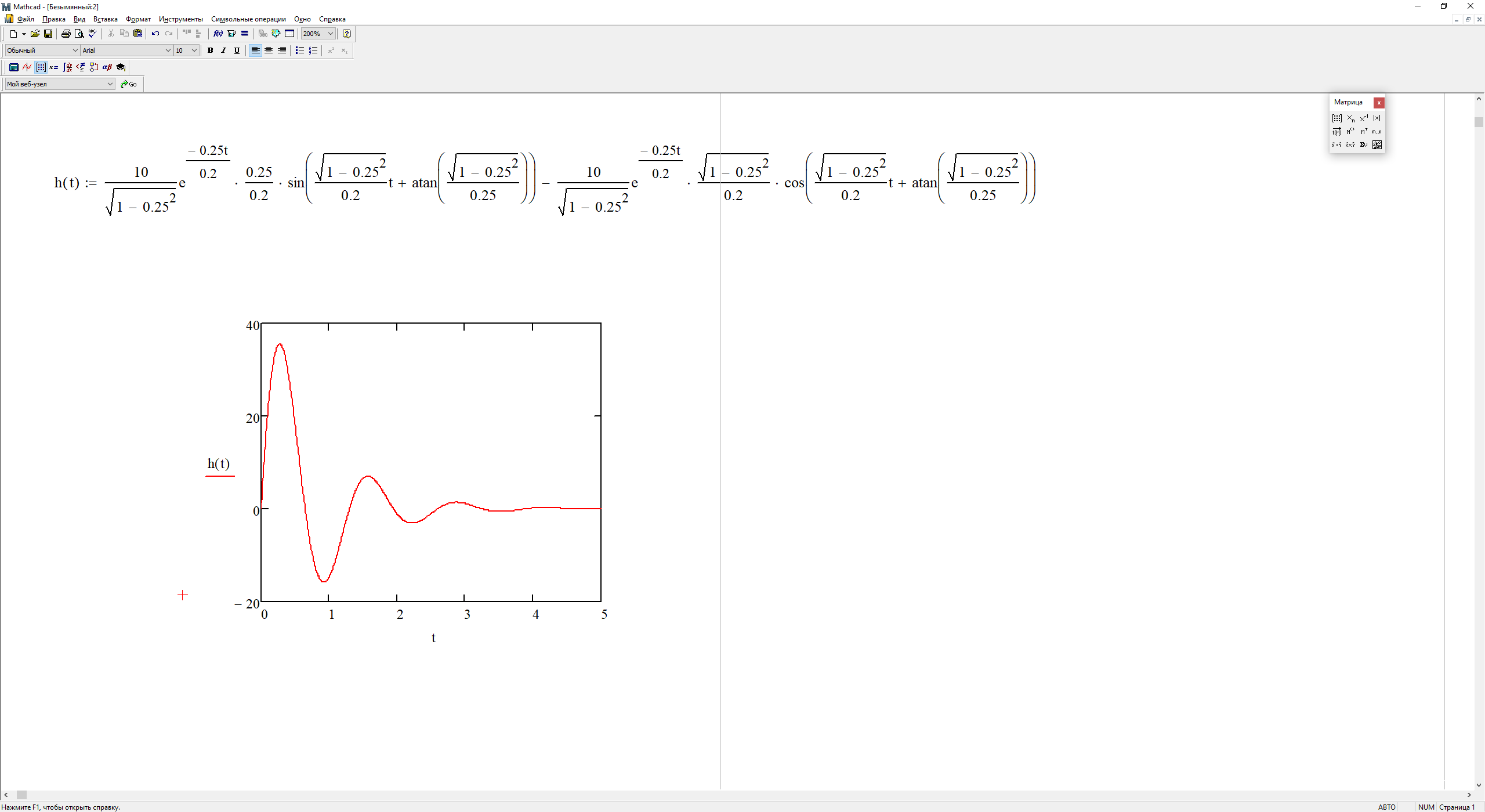
Рисунок 3.20 - график переходной функции.
Амплитудная частотная характеристика (АЧХ):



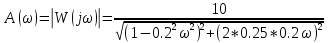
На рисунке 3.21 представлен график АЧХ.



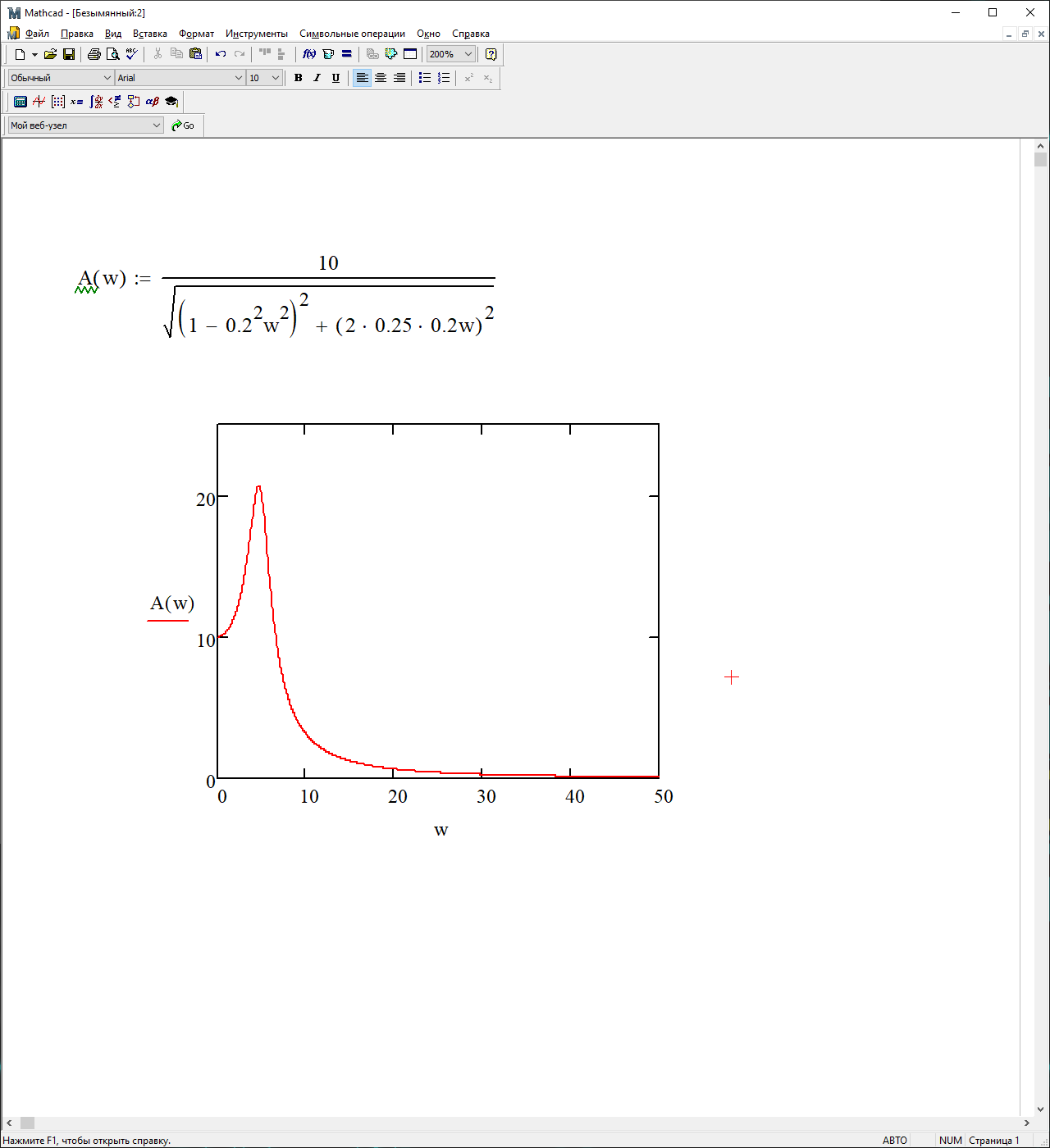
Рисунок 3.21 - график АЧХ.
Фазовая частотная характеристика (ФЧХ):



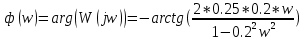
На рисунке 3.22 представлен график ФЧХ.


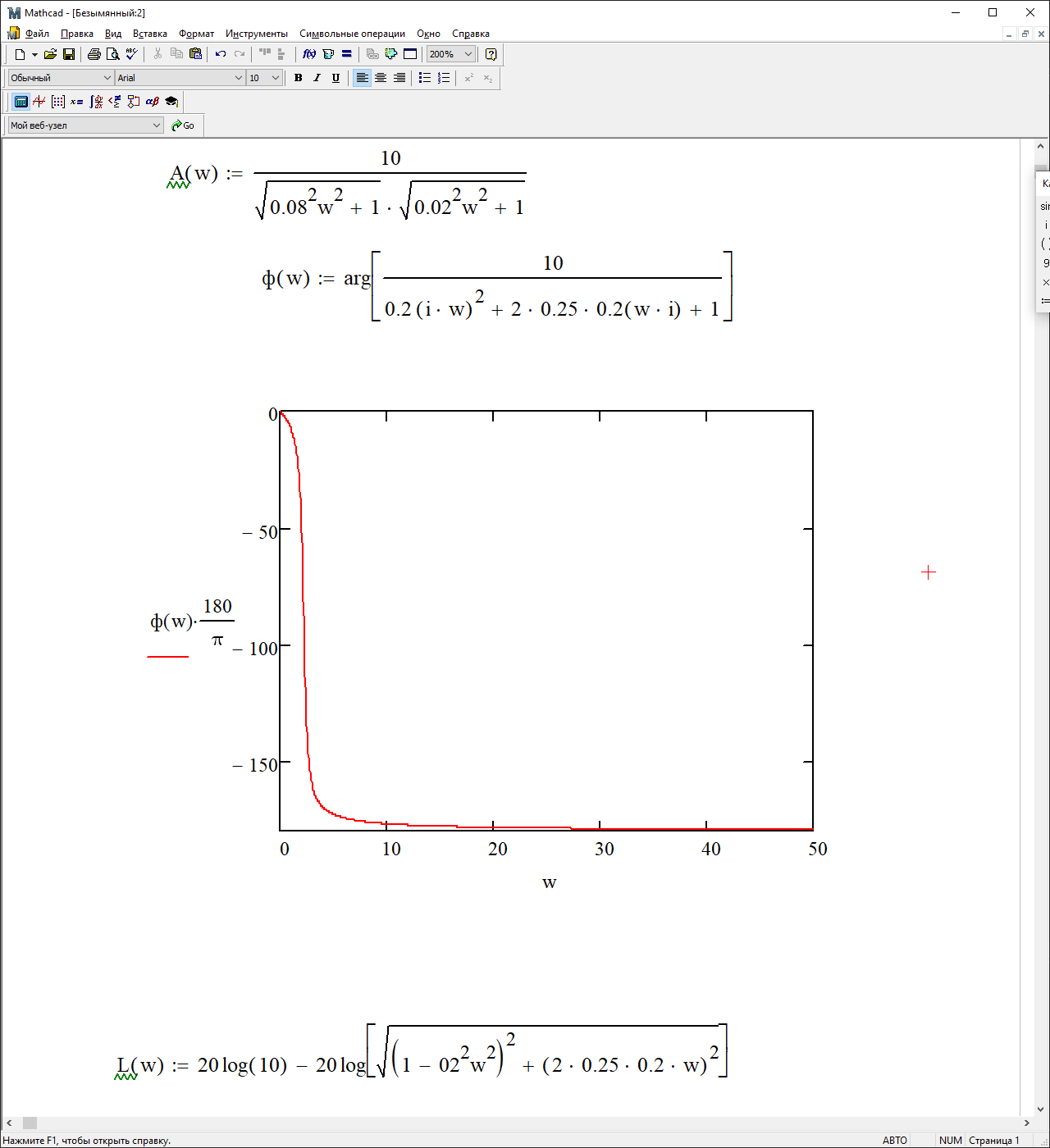
Рисунок 3.22 - график ФЧХ.

Логарифмическая амплитудная частотная характеристика (ЛАЧХ):


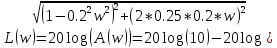
На рисунке 3.23 представлен график ЛАЧХ.


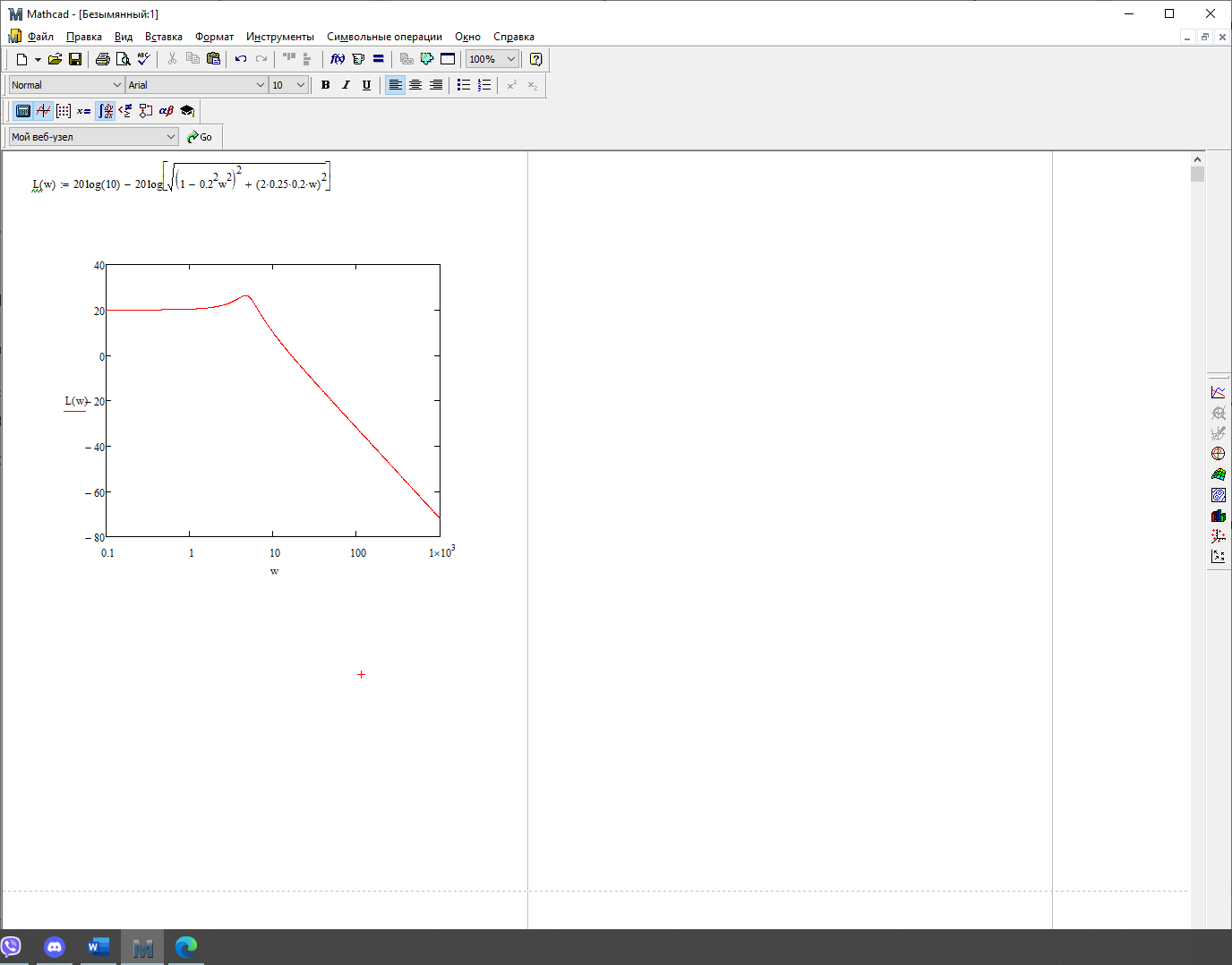
Рисунок 3.23 - график ЛАЧХ.
Амплитудно-фазовая частотная характеристика (АФЧХ):



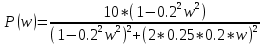
На рисунке 3.24 представлен график АФЧХ.



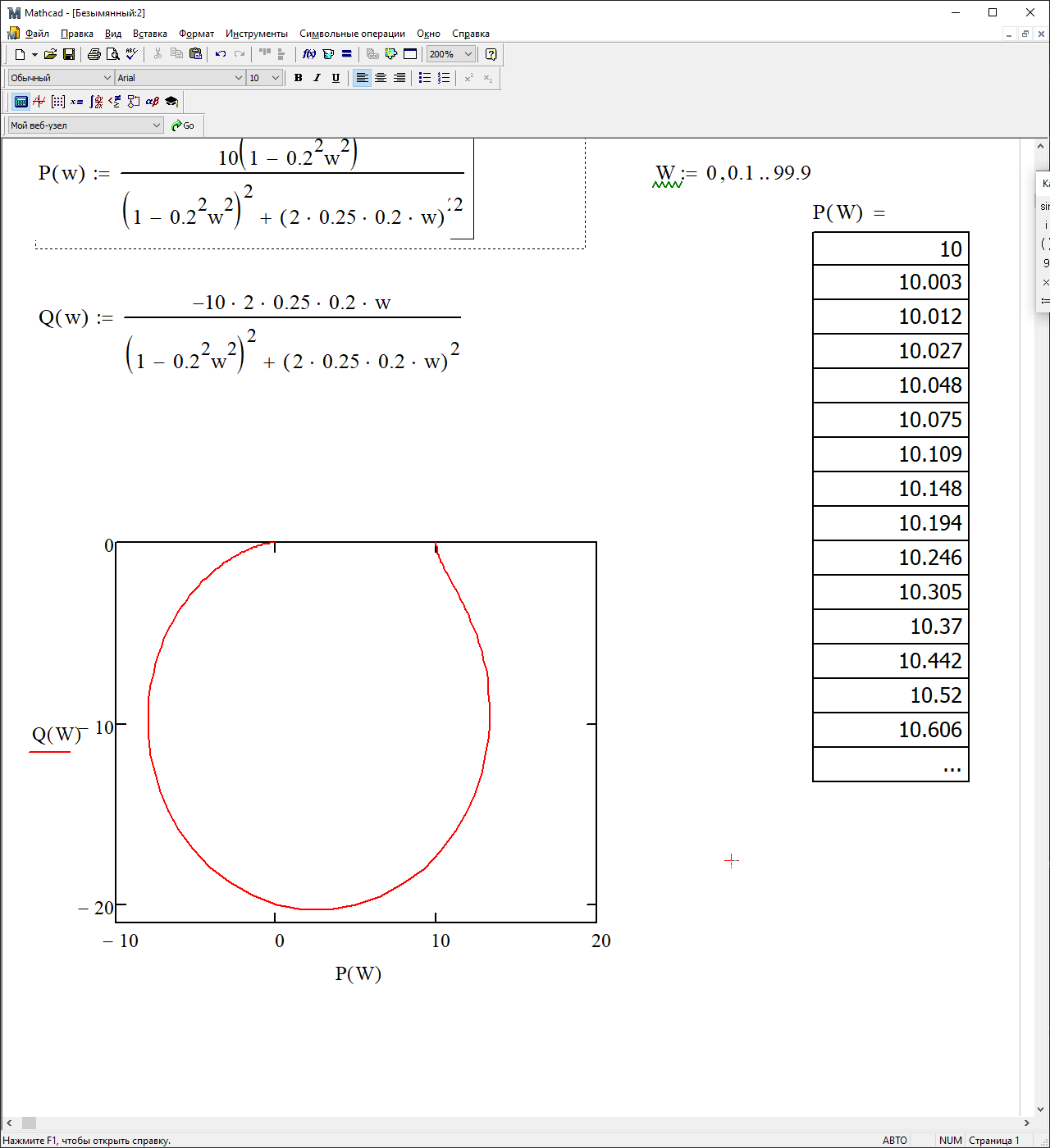
Рисунок 3.24 - график АФЧХ.

3.5. Идеальное интегрирующее звено

Произведем замену , чтобы перейти к операторному уравнению, получим:

pF1(p) =10F(p).

Передаточная функция:




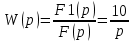
Переходная и весовая функции:

h(t)=10t.

---