Файл: Отчет лабораторная работа 1 типовые звенья и их характеристики выполнил Студент гр. 5101 07 мая 2023 г. Проверил.docx
Добавлен: 30.11.2023
Просмотров: 45
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
На рисунке 3.25 представлен график весовой функции
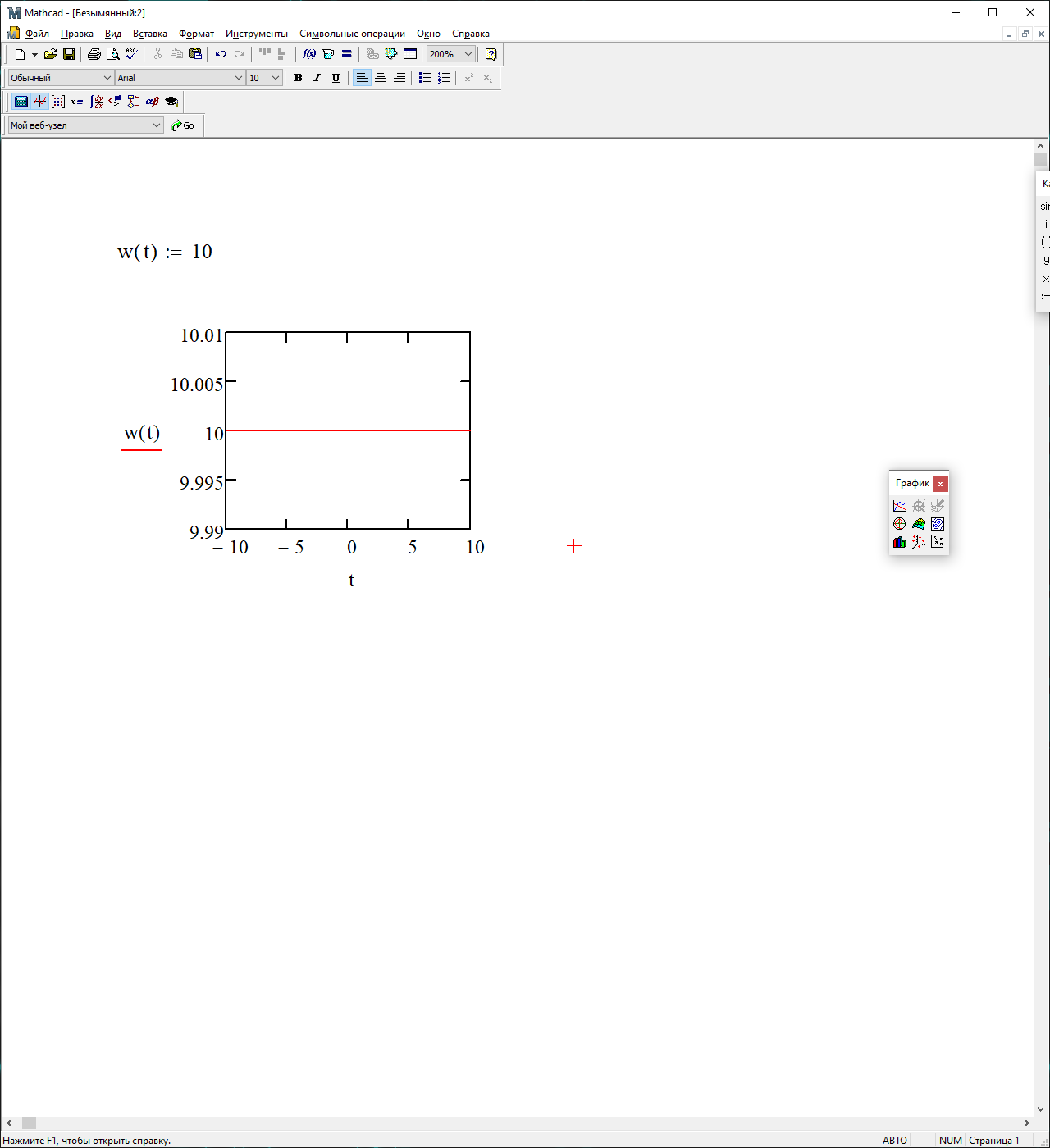
Рисунок 3.25 - график весовой функции.
На рисунке 3.26 представлен график переходной характеристики
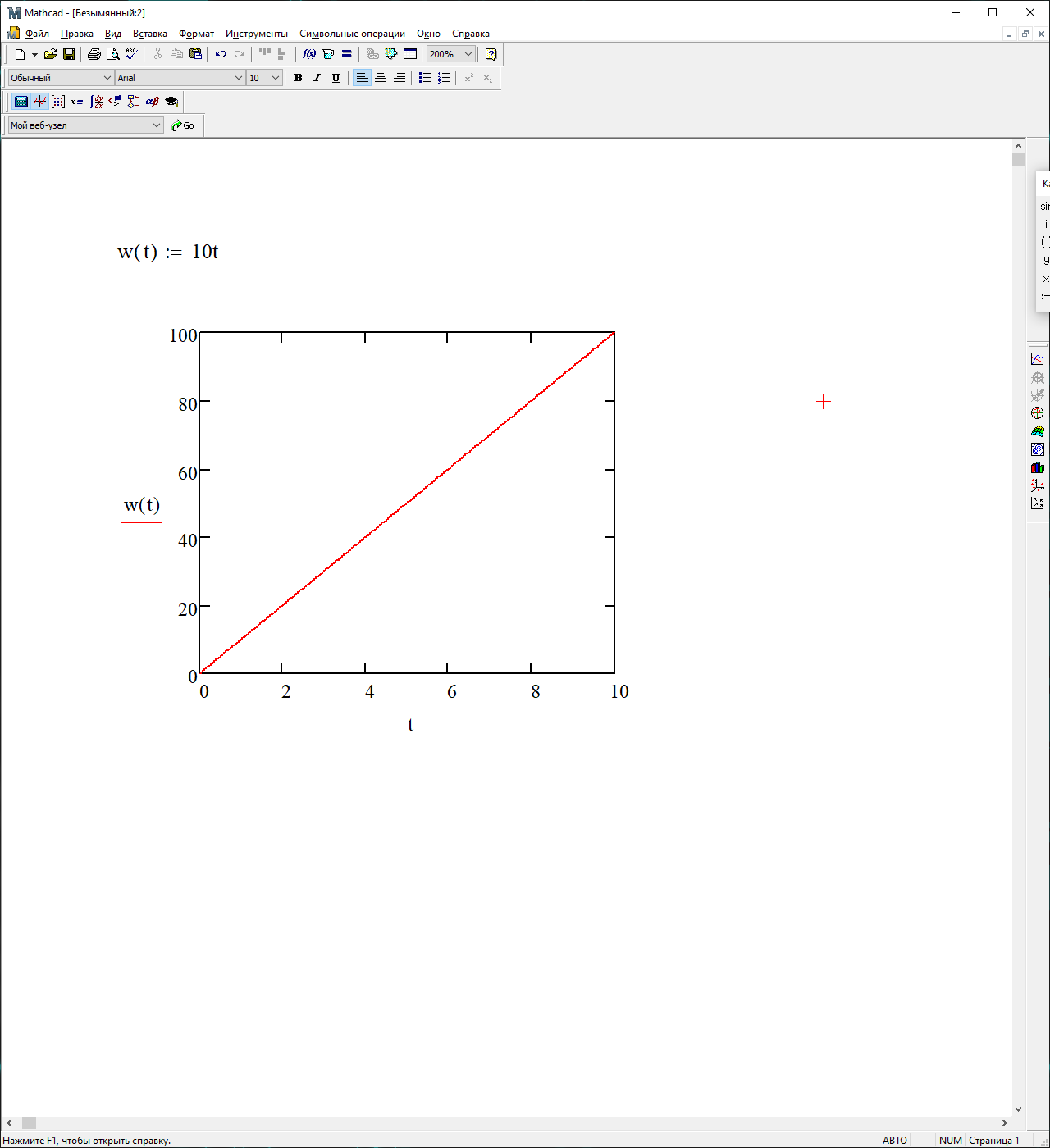
Рисунок 3.26 - график переходной характеристики.
Амплитудная частотная характеристика (АЧХ):
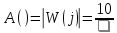
На рисунке 3.27 представлен график АЧХ
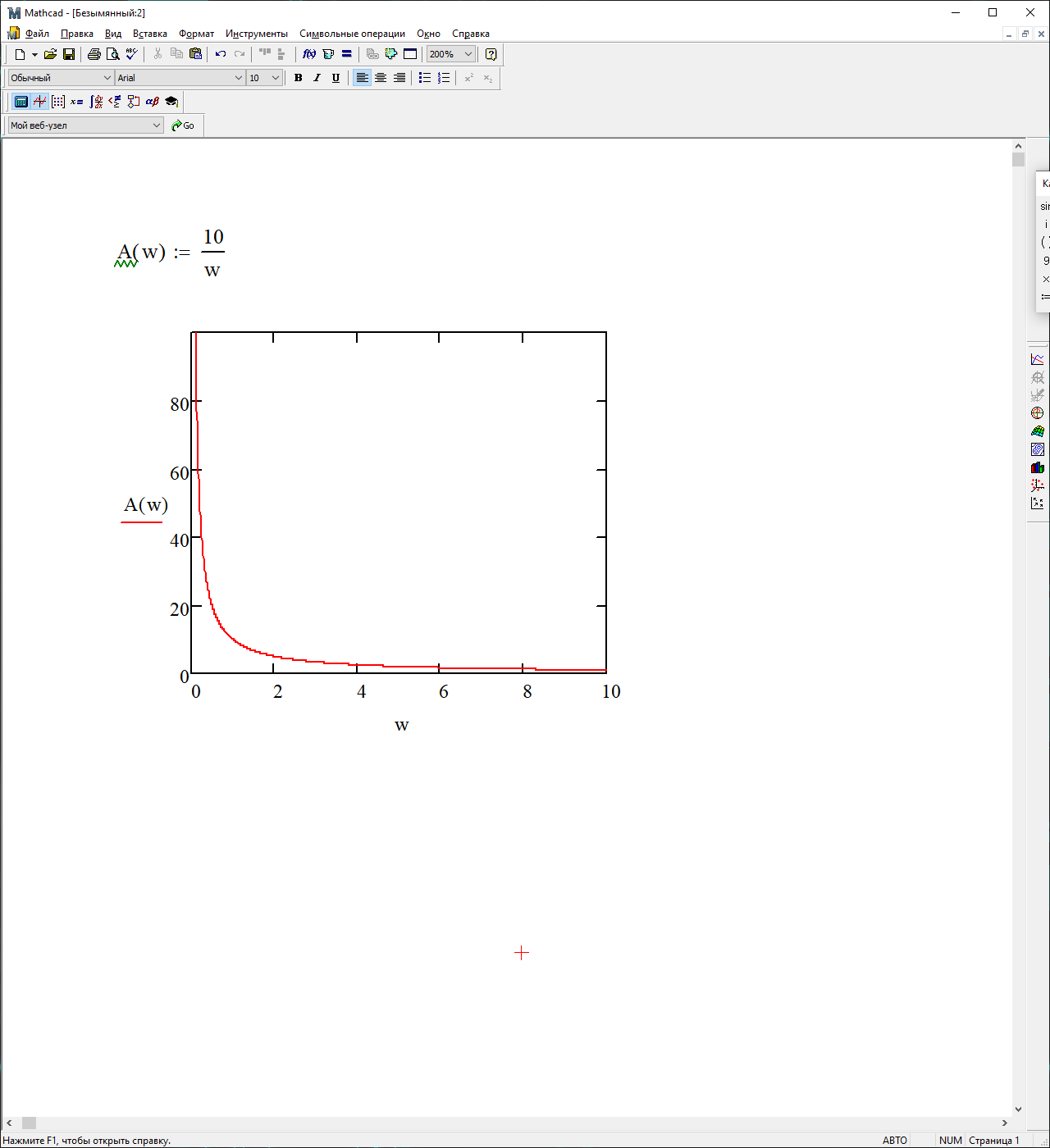
Рисунок 3.27 – График АЧХ
Фазовая частотная характеристика (ФЧХ)
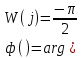
На рисунке 3.28 представлен график ФЧХ
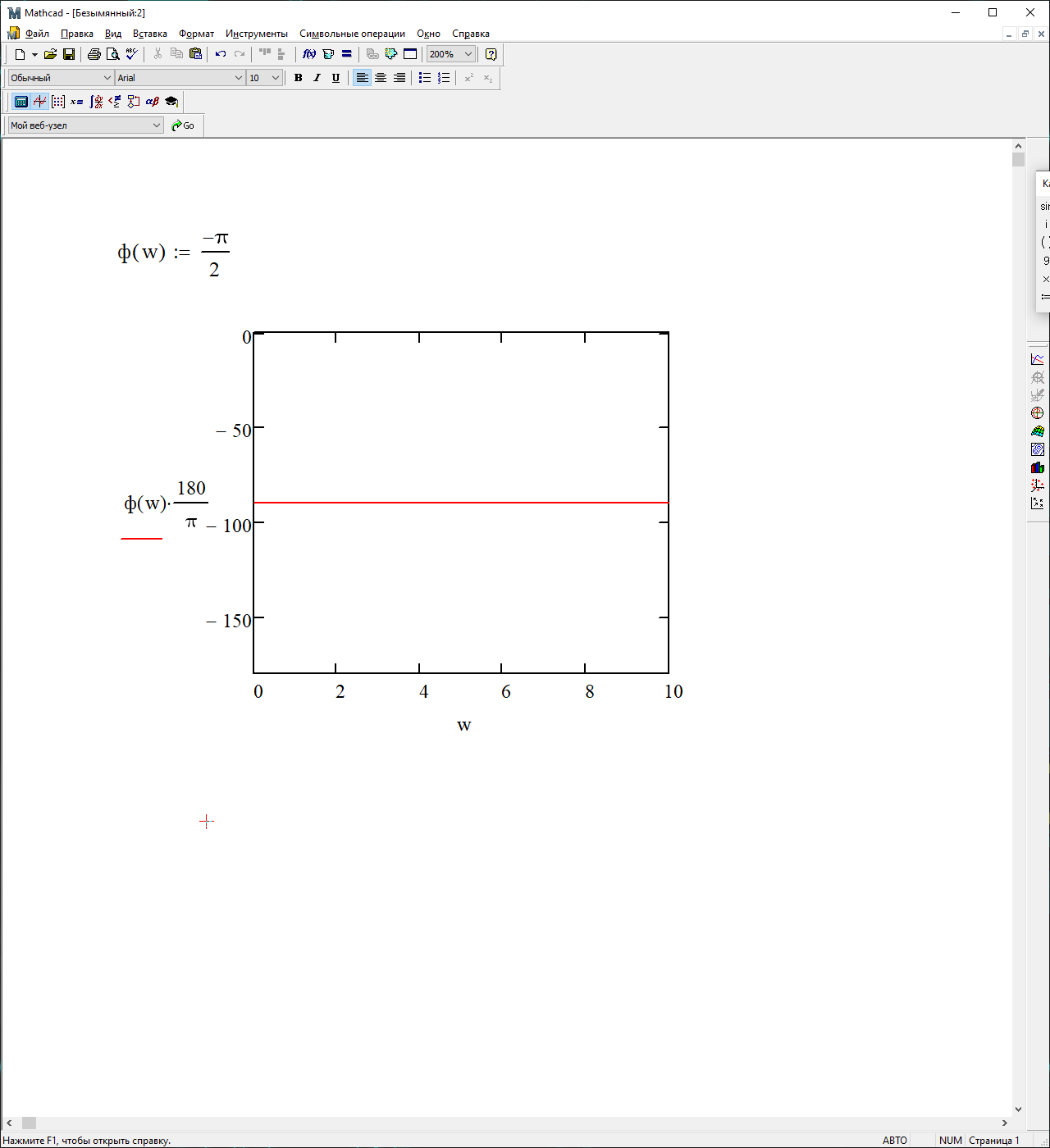
Рисунок 3.28 – График ФЧХ
Логарифмическая амплитудная частотная характеристика (ЛАЧХ):
L() = 20lg(A()) = 20lg10 − 20lg
На рисунке 3.29 представлен график ЛАЧХ
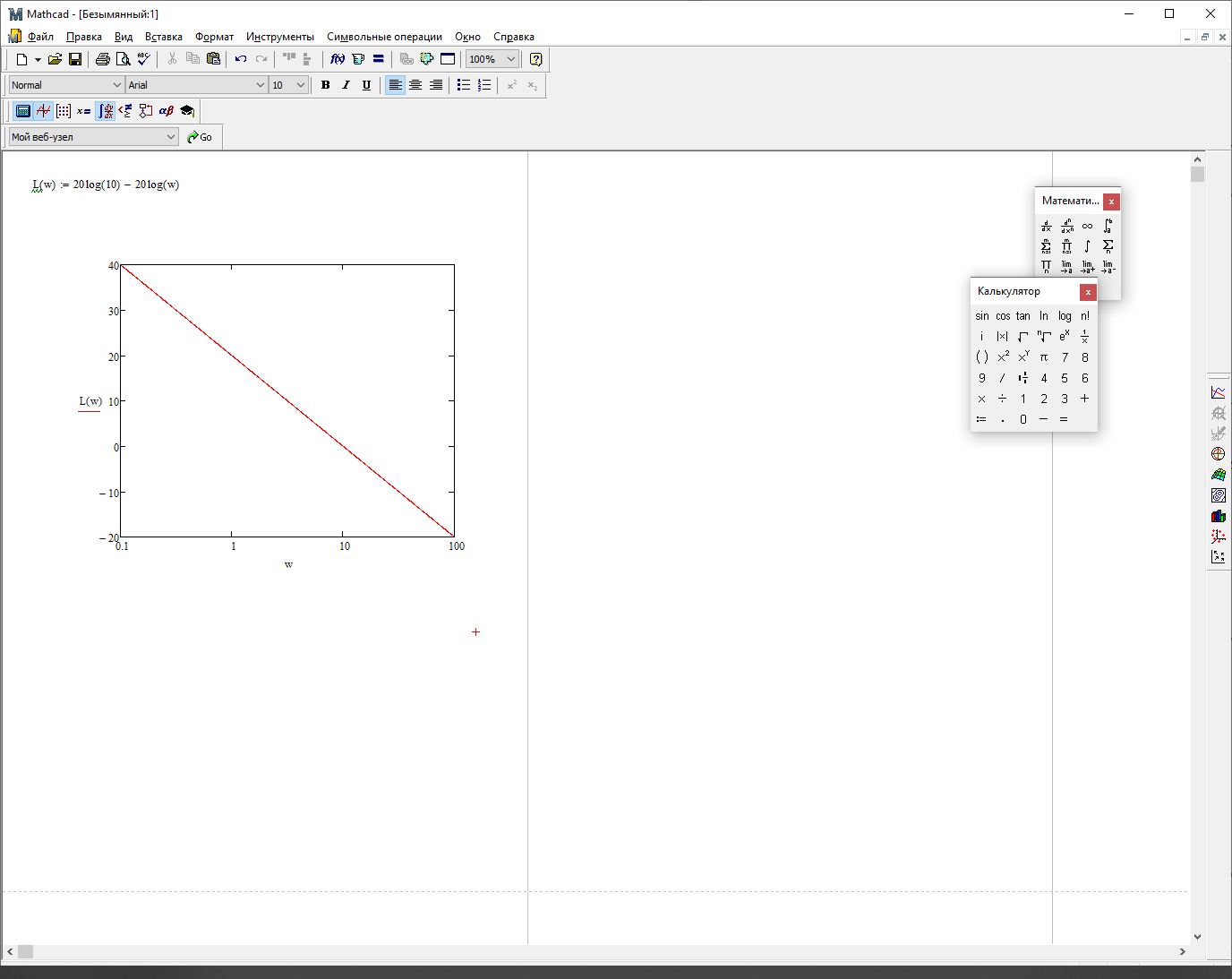
Рисунок 29 – График ЛАЧХ
Амплитудно-фазовая частотная характеристика (АФЧХ):
P()=0
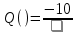
На рисунке 3.30 представлен график АФЧХ
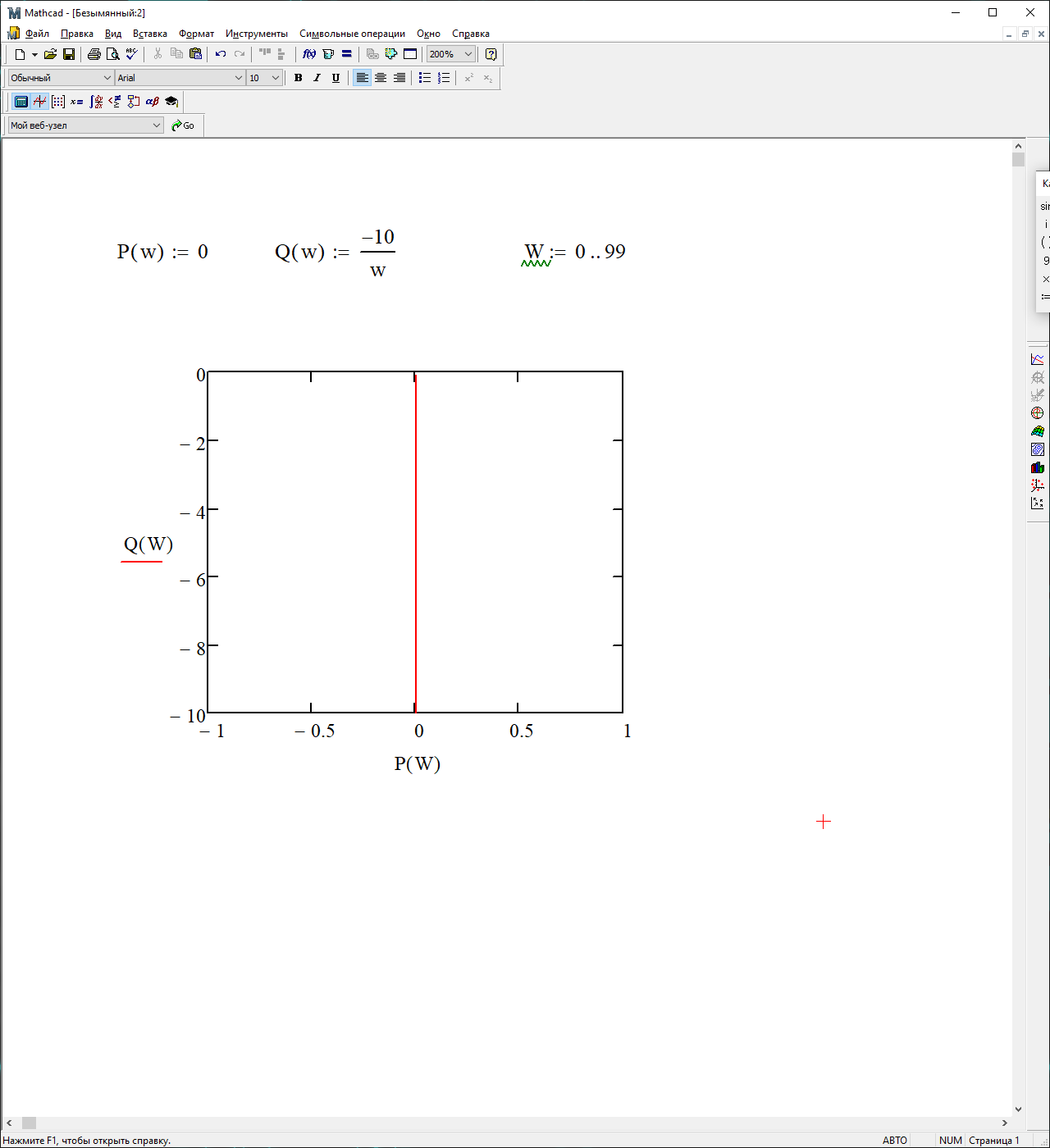
Рисунок 3.30 – График АФЧХ
3.6. Интегрирующее звено с замедлением
Произведем замену
 , чтобы перейти к операторному уравнению, получим:
, чтобы перейти к операторному уравнению, получим:(0.1p2+p)F1(p)=10F(p)
Передаточная функция:
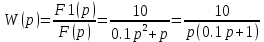
Переходная и весовая функции:
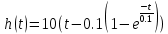
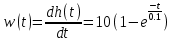
На рисунке 3.31 представлен график весовой функции
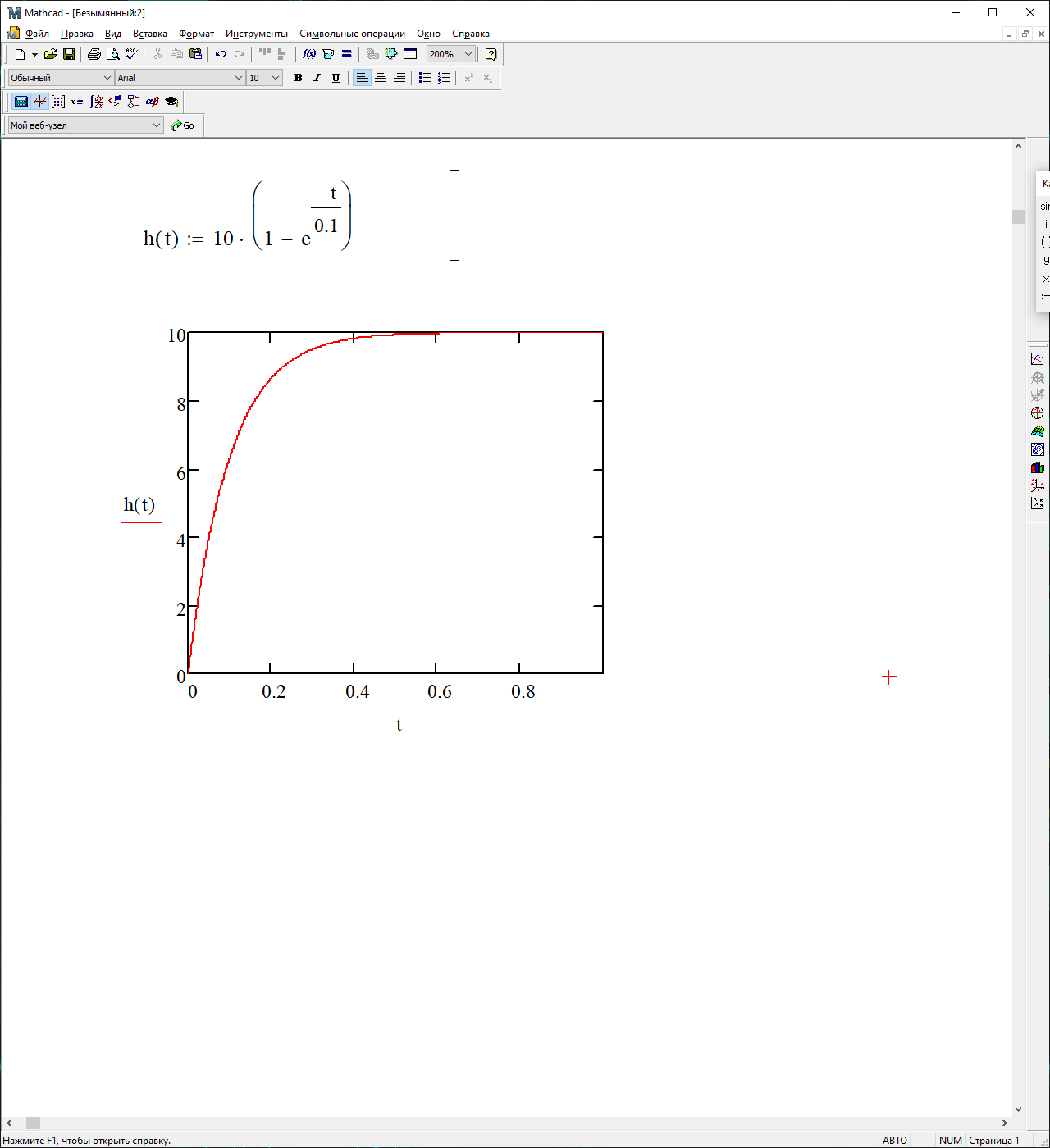
Рисунок 3.31 – График весовой функции
На рисунке 3.32 представлен график переходной характеристики
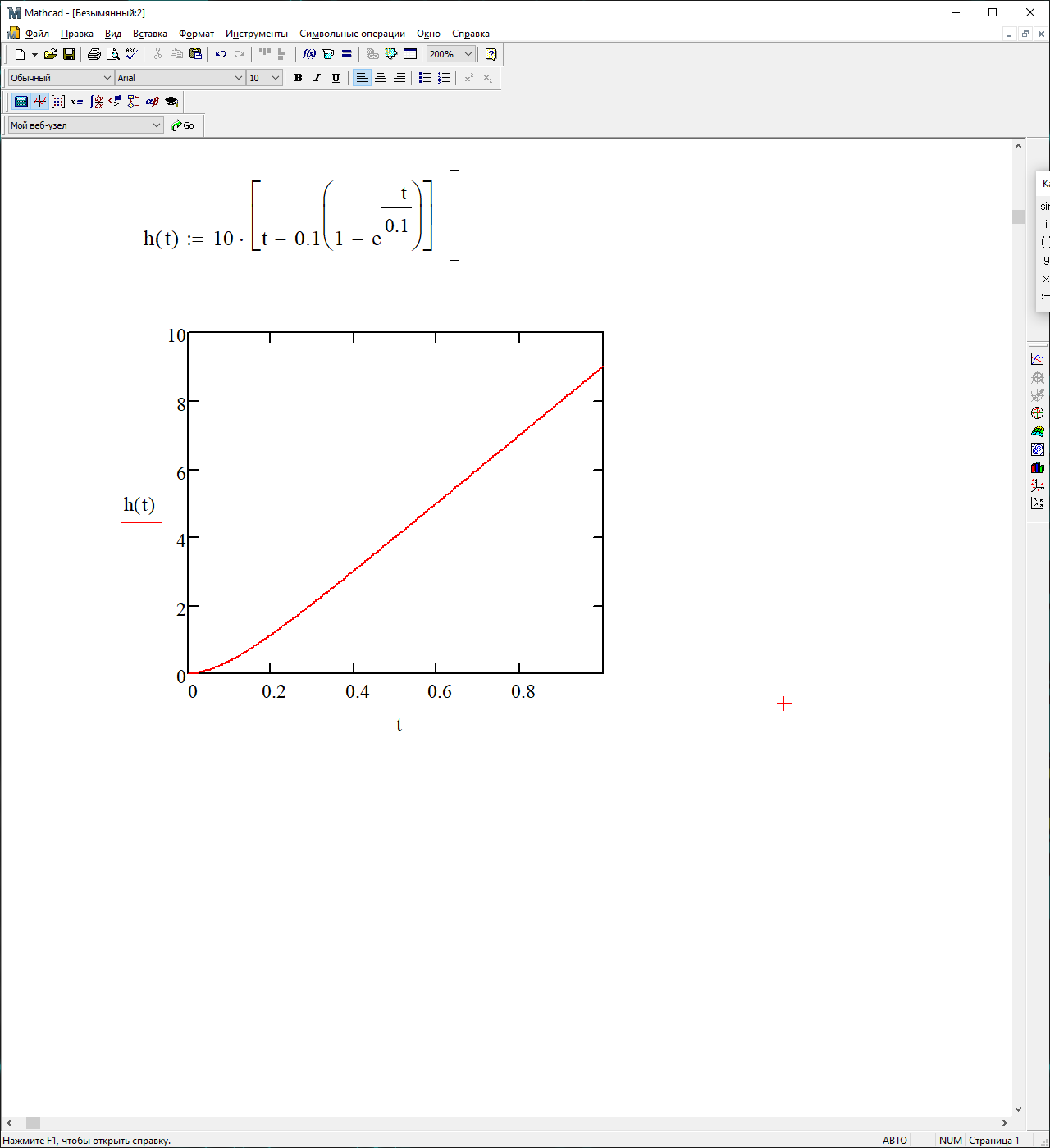
Рисунок 3.32 – График переходной характеристики
Амплитудная частотная характеристика (АЧХ):
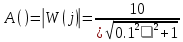
На рисунке 3.33 представлен график АЧХ
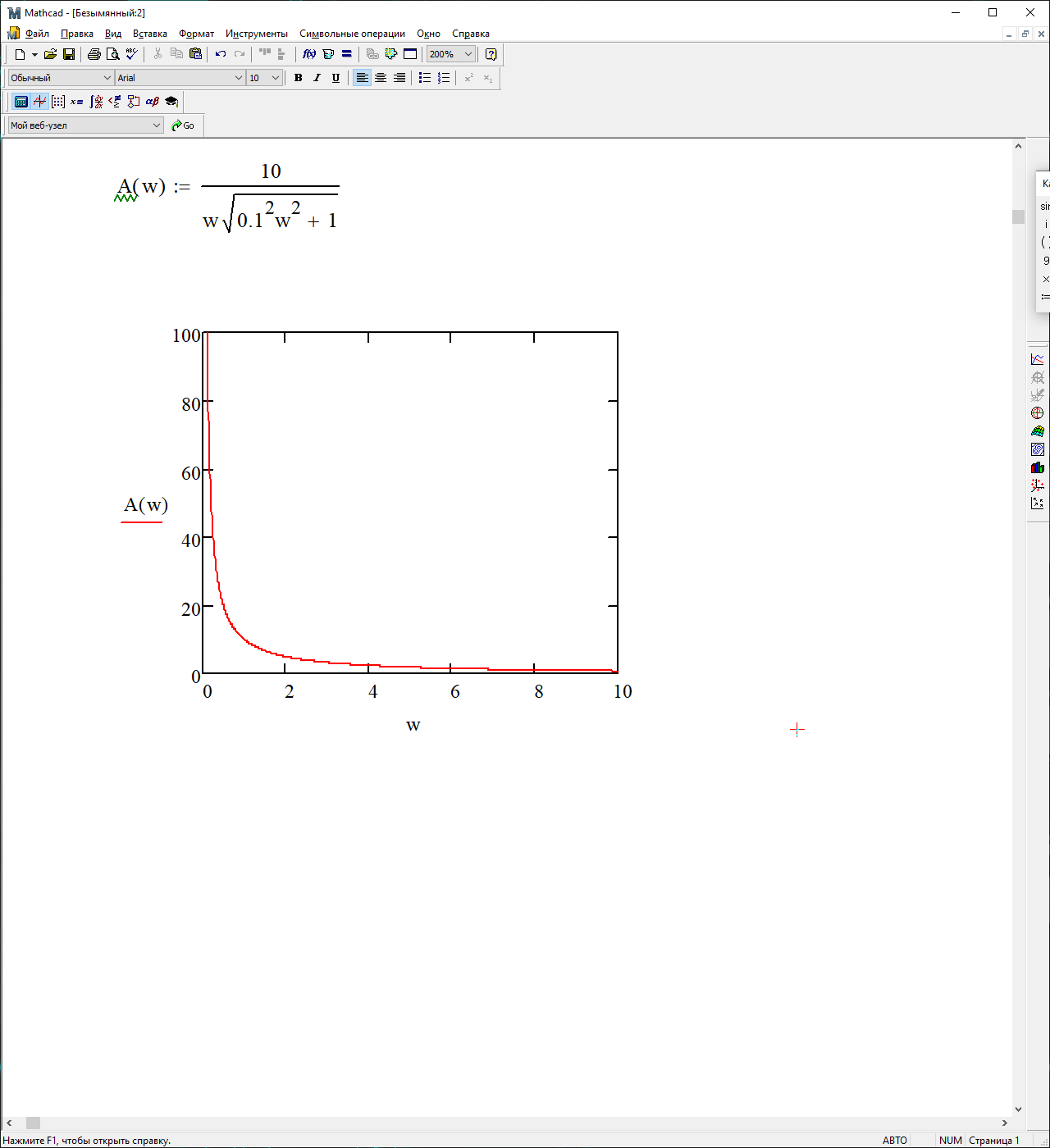
Рисунок 3.33 – График АЧХ
Фазовая частотная характеристика (ФЧХ)
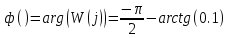
На рисунке 3.34 представлен график ФЧХ
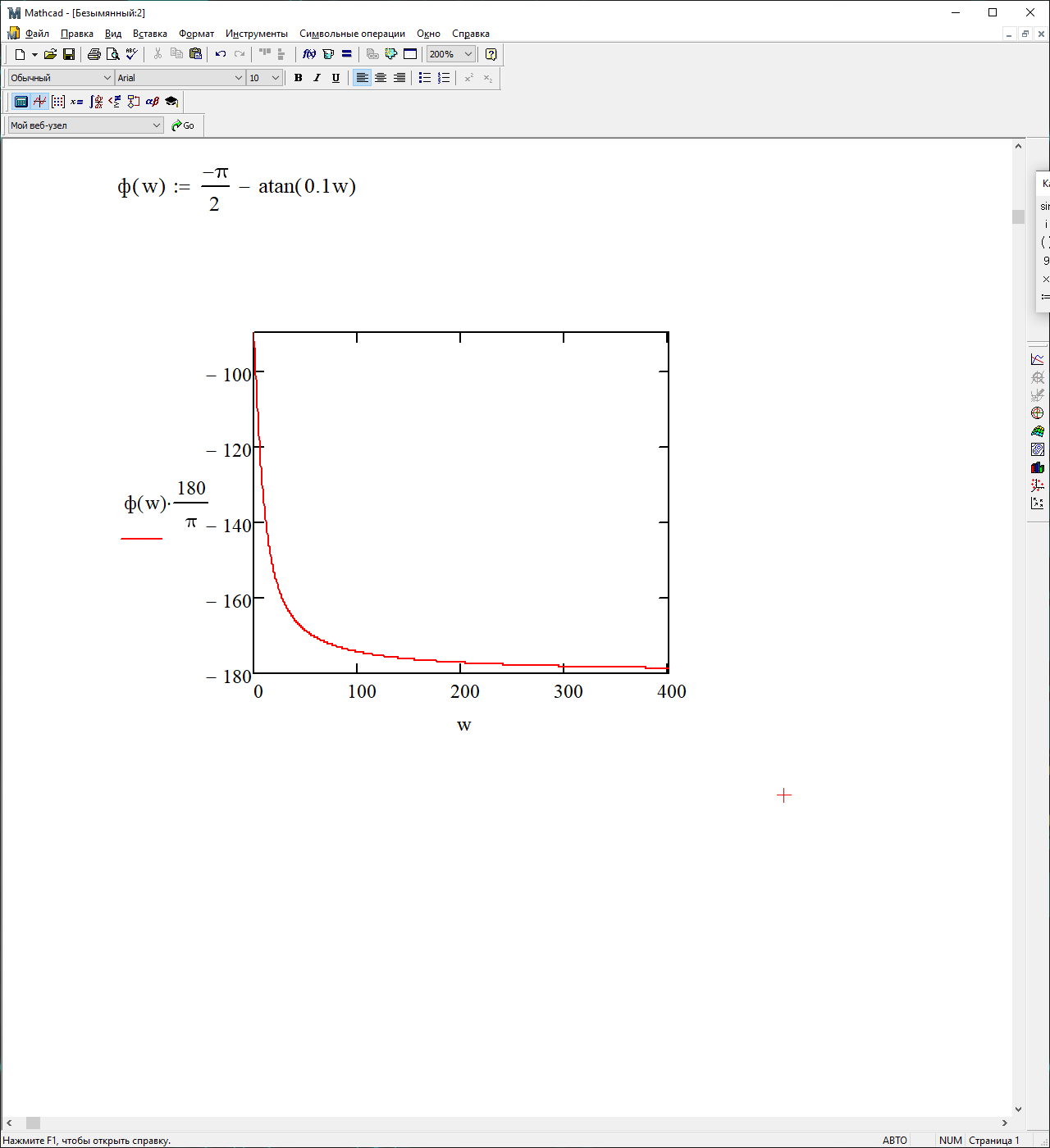
Рисунок 3.34 – График ФЧХ
Логарифмическая амплитудная частотная характеристика (ЛАЧХ):
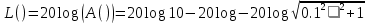
На рисунке 3.35 представлен график ЛАЧХ
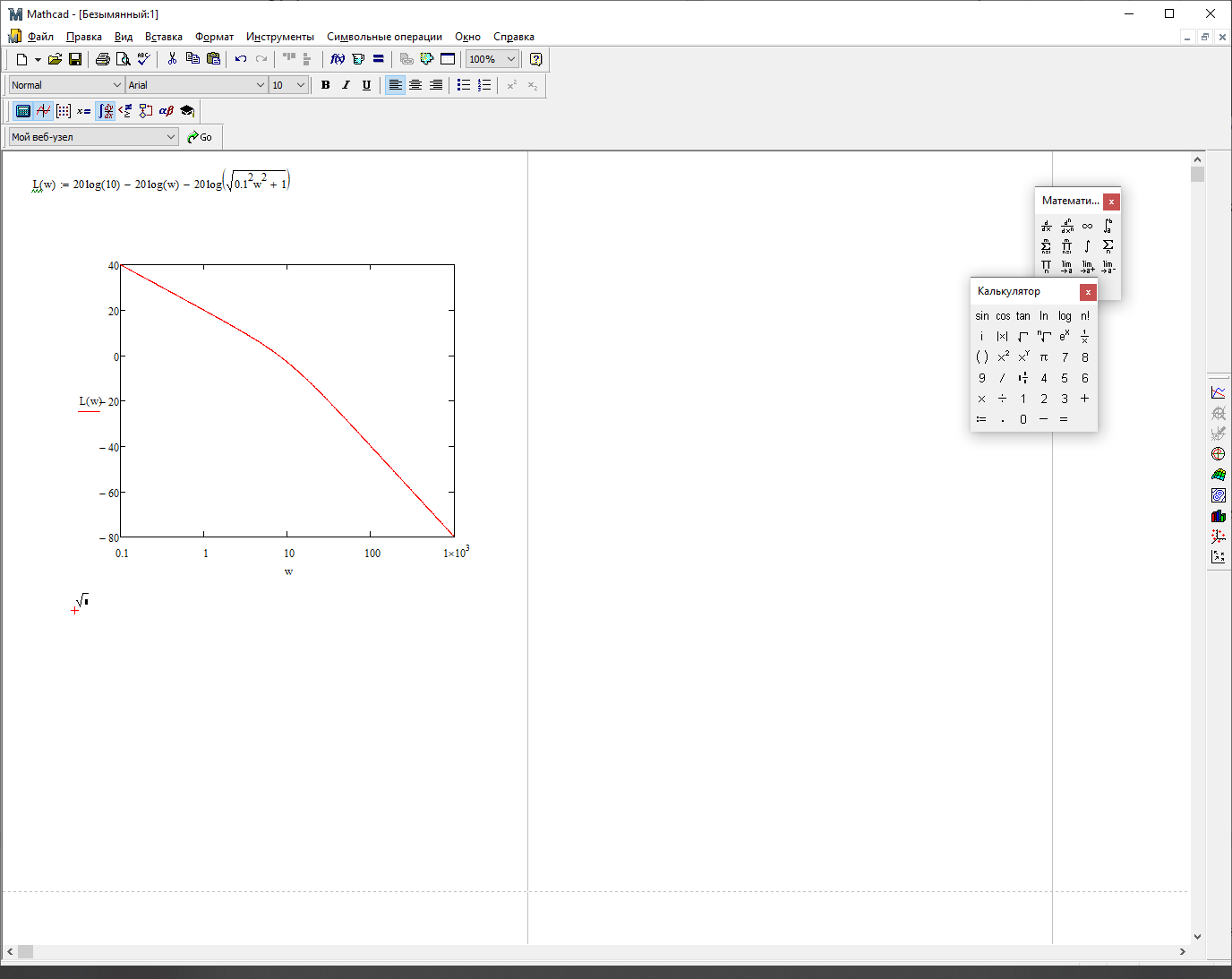
Рисунок 3.35 – График ЛАЧХ
Амплитудно-фазовая частотная характеристика (АФЧХ):
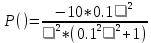
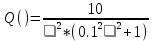
На рисунке 3.36 представлен график АФЧХ
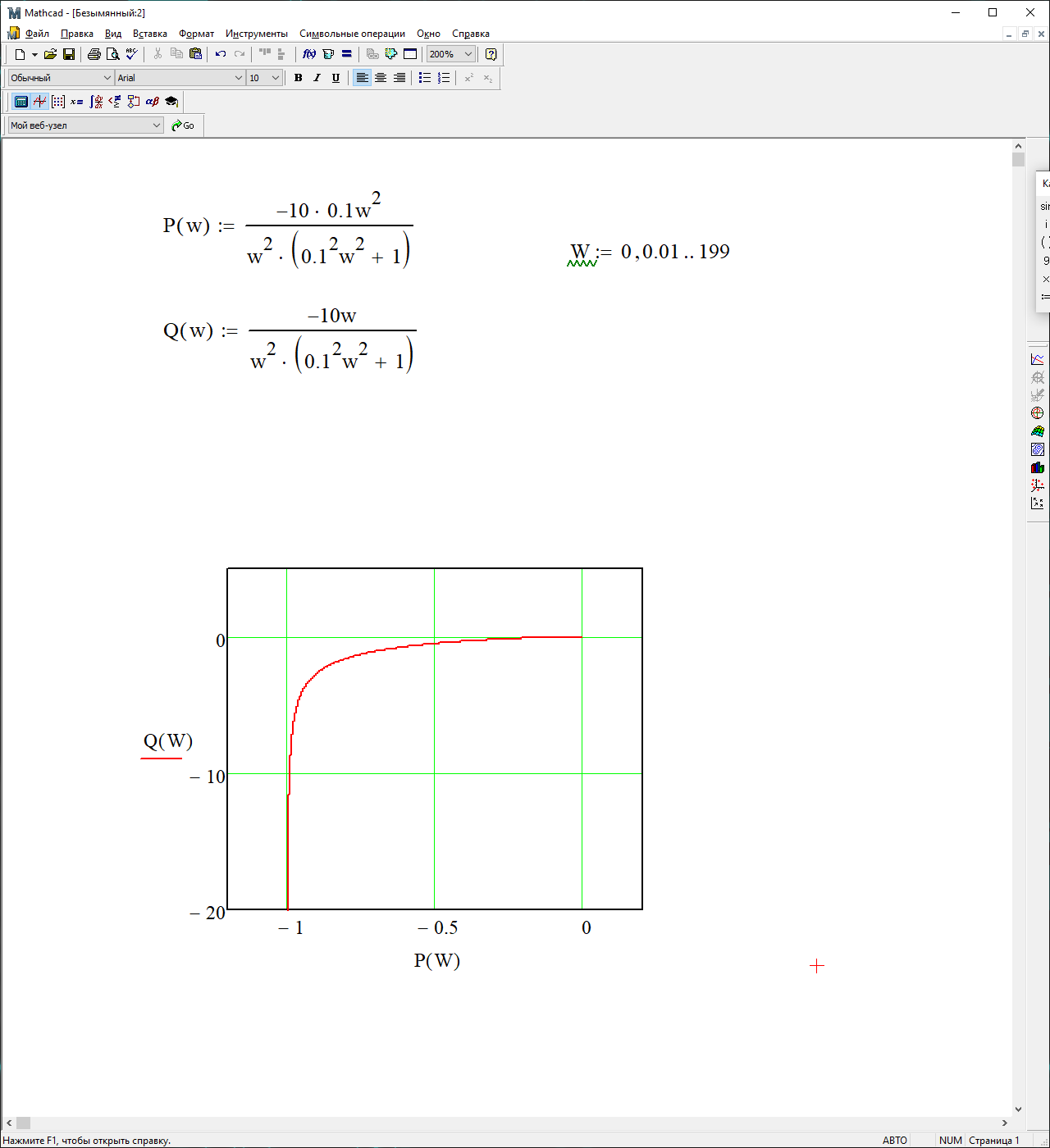
Рисунок 3.36 – График АФЧХ
3.7. Идеальное дифференцирующее
Произведем замену
 , чтобы перейти к операторному уравнению, получим:
, чтобы перейти к операторному уравнению, получим:F1(p)=10pF(p)
Передаточная функция:
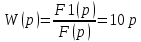
Переходная и весовая функции:
h(t)= 10*(t)
w(t)= 10*’(t)
На рисунке 3.37 представлен график весовой функции
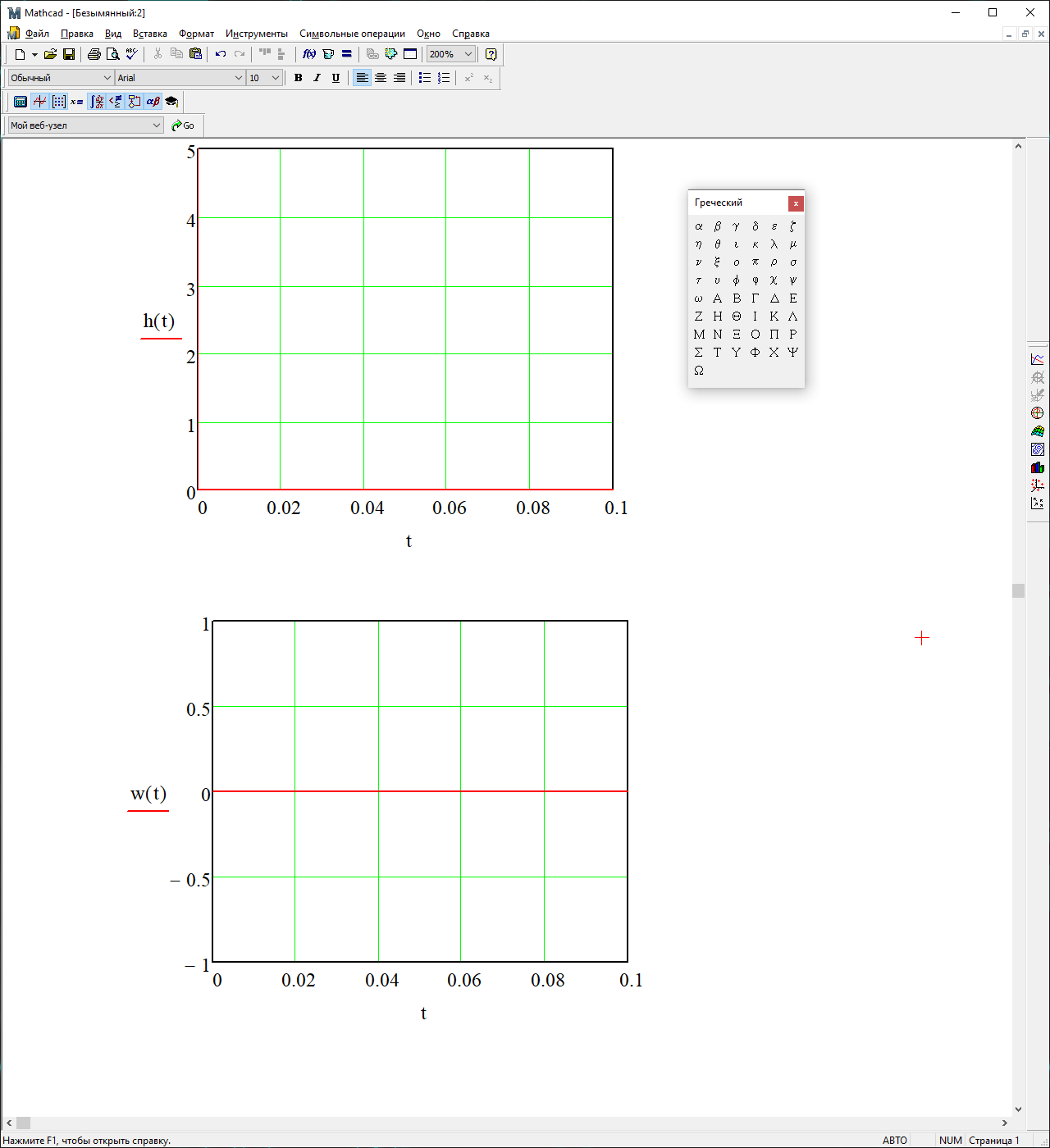
Рисунок 3.37 – График весовой функции
На рисунке 3.38 представлен график переходной характеристики
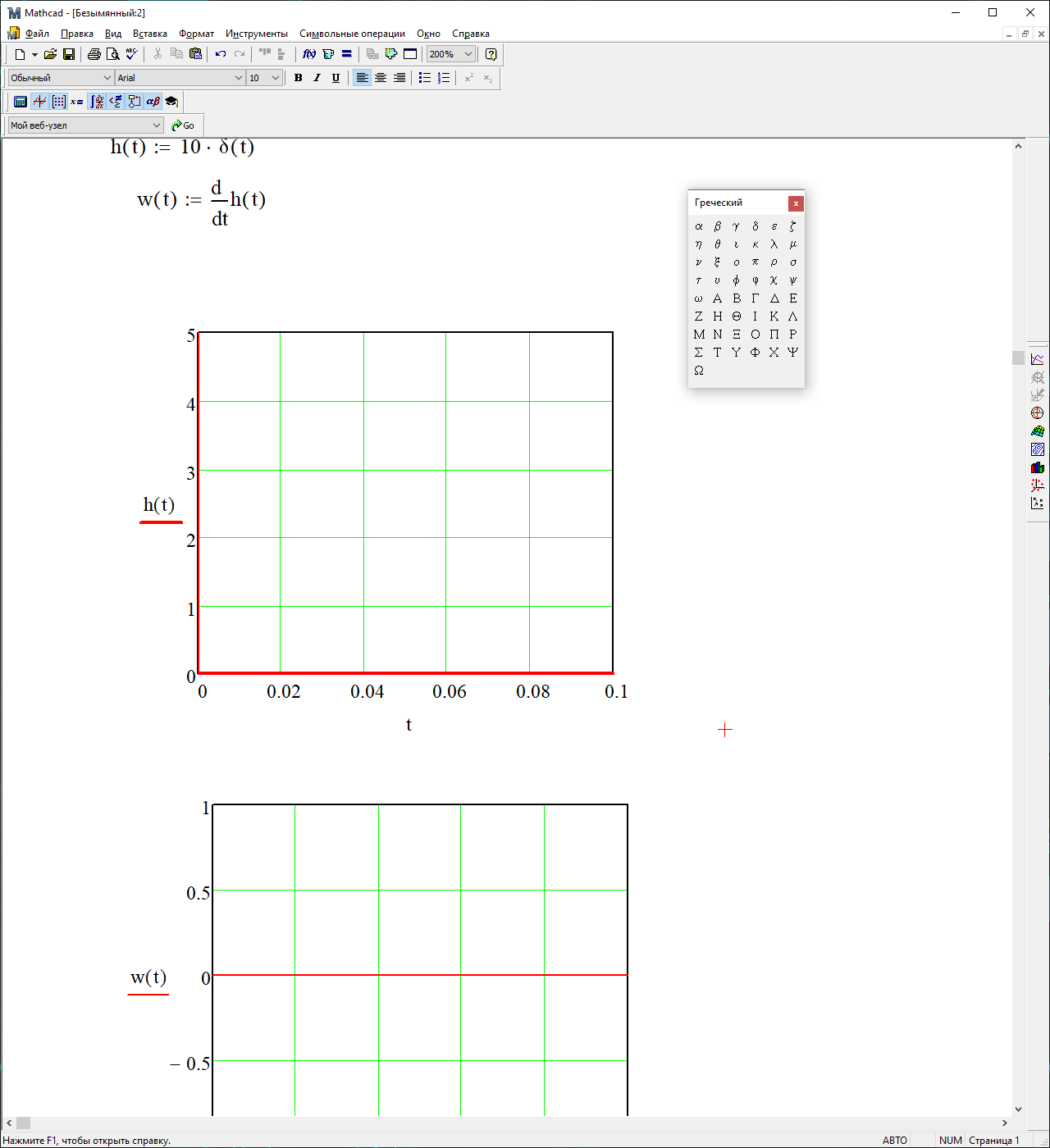
Рисунок 3.38 – График переходной характеристики
Амплитудная частотная характеристика (АЧХ)
A() = |W(j)| = 10.
На рисунке 3.39 представлен график АЧХ
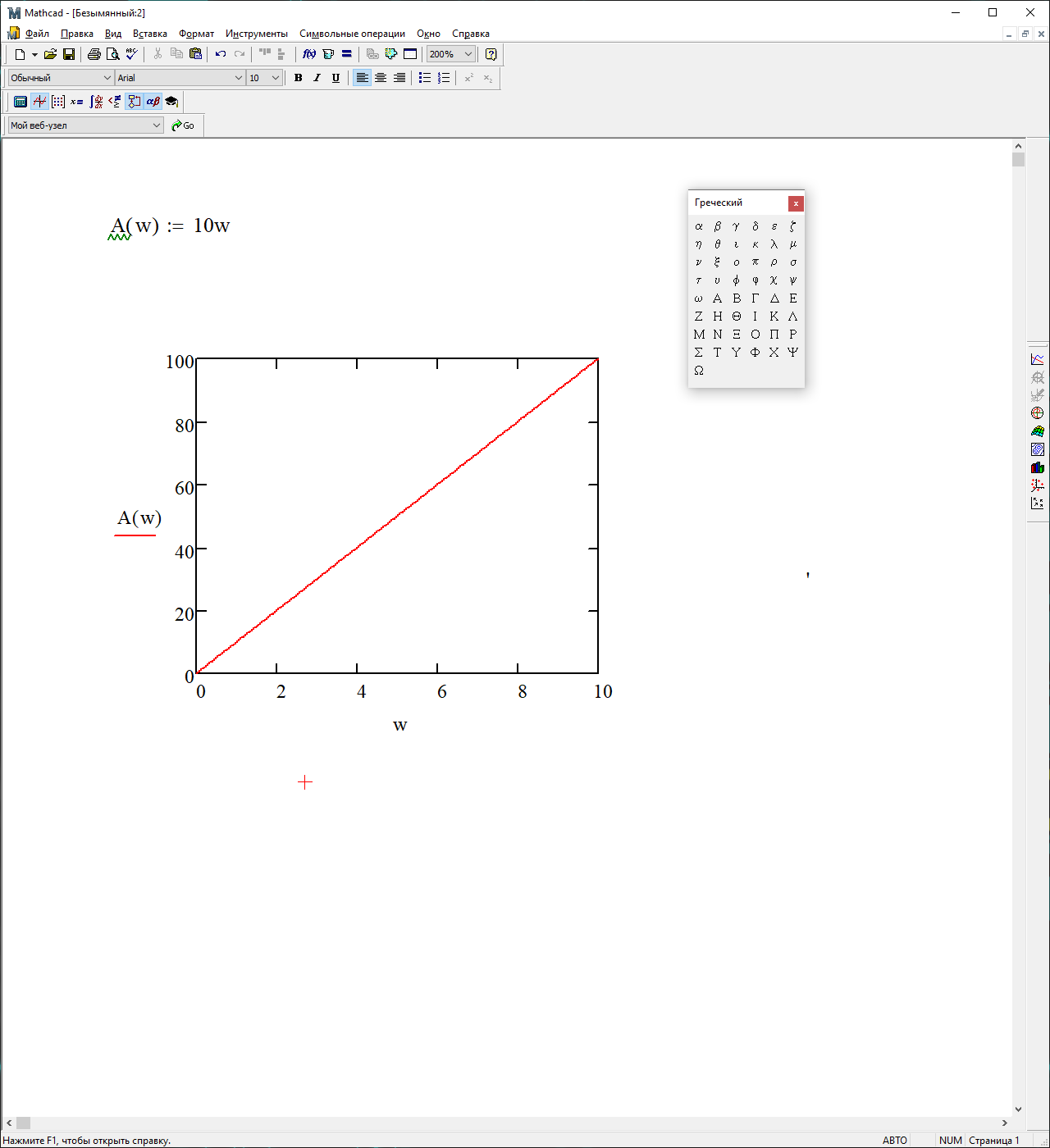
Рисунок 39 – График АЧХ
Фазовая частотная характеристика (ФЧХ):
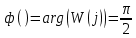
На рисунке 3.40 представлен график ФЧХ
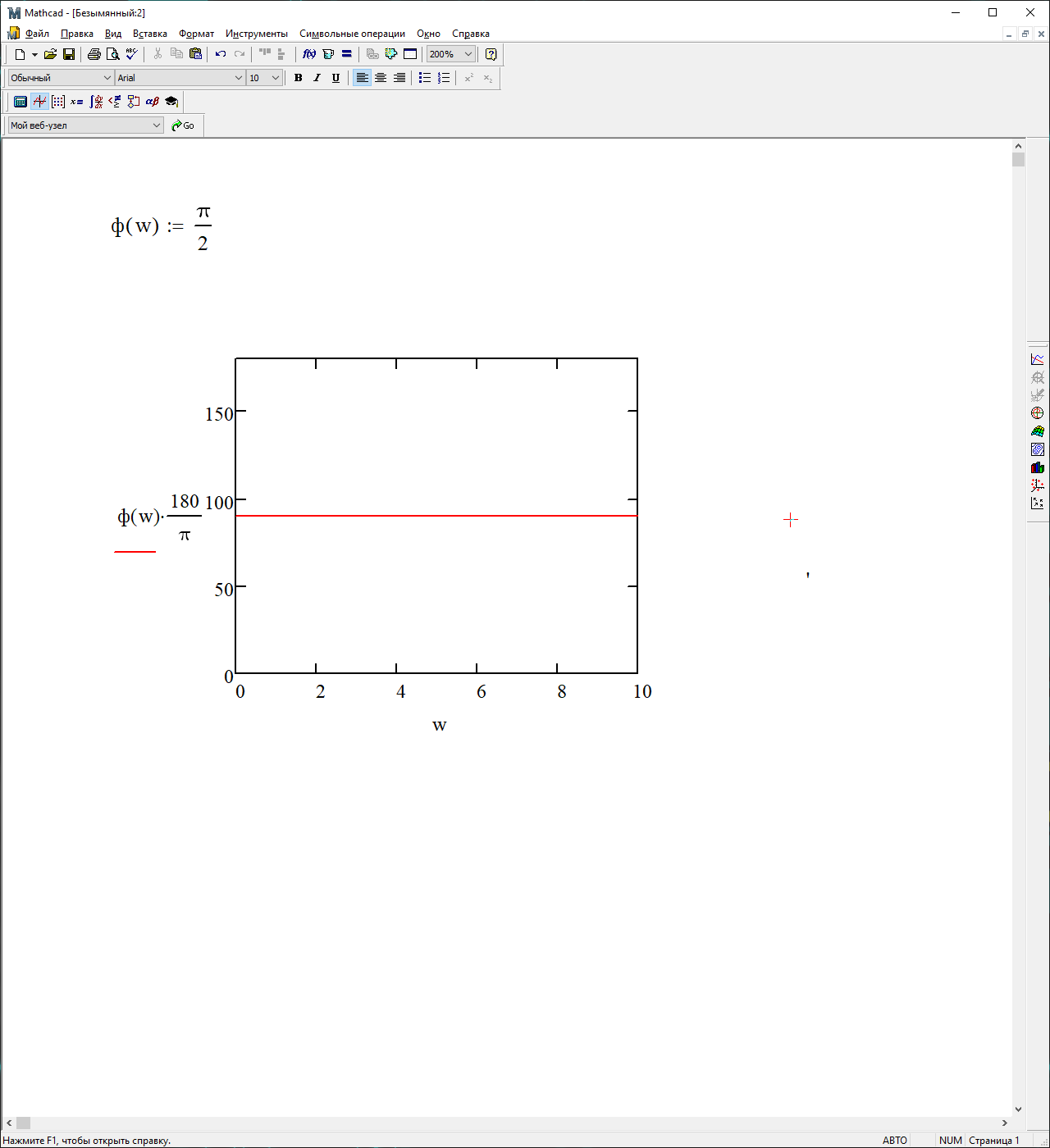
Рисунок 3.40 – График ФЧХ
Логарифмическая амплитудная частотная характеристика (ЛАЧХ):
L(
 ) = 20lg(A(
) = 20lg(A( )) = 20lg10 + 20lg
)) = 20lg10 + 20lg .
.На рисунке 3.41 представлен график ЛАЧХ
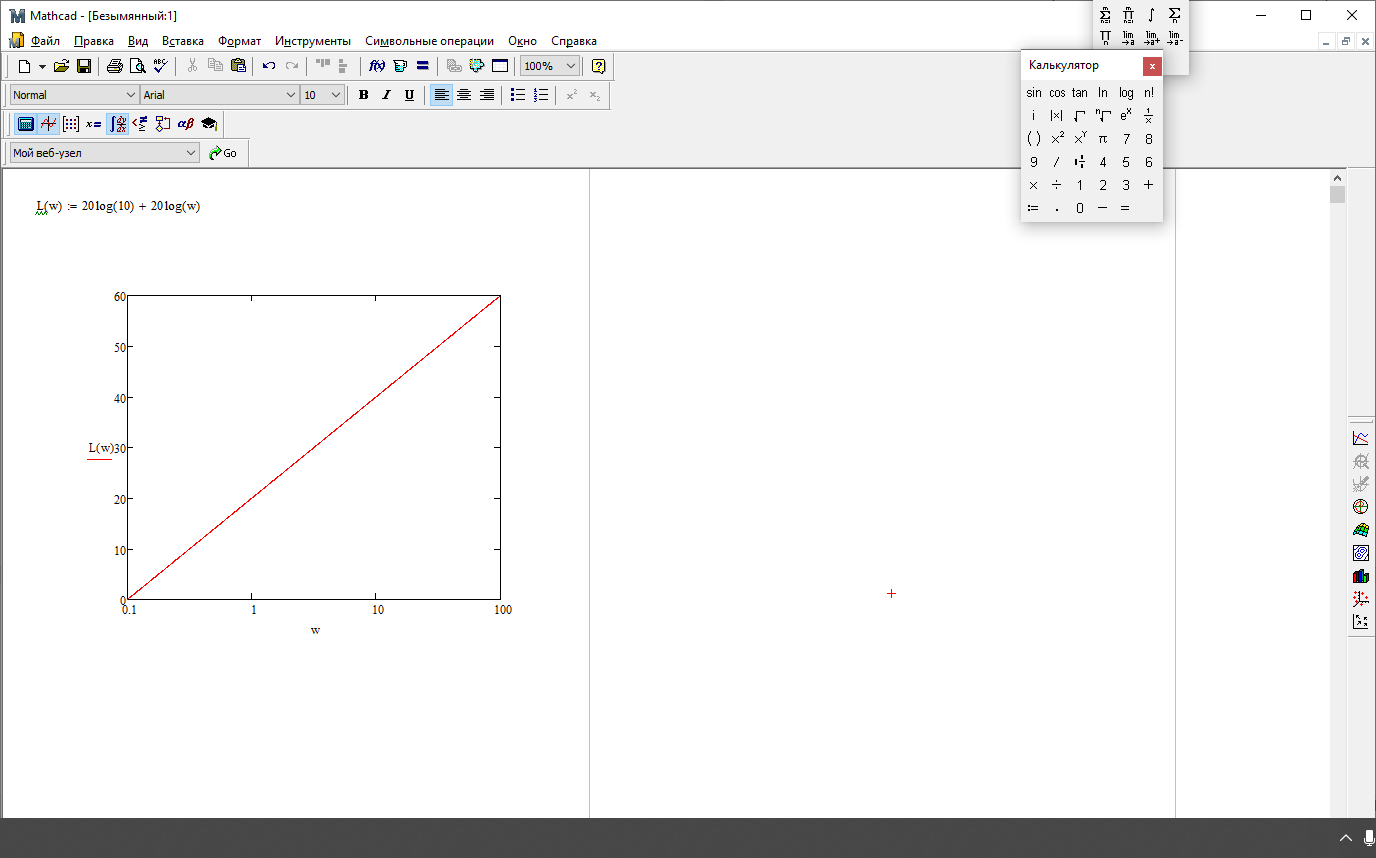
Рисунок 3.41 – График ЛАЧХ
Амплитудно-фазовая частотная характеристика (АФЧХ):
P() = 0
Q() =10
На рисунке 3.42 представлен график АФЧХ
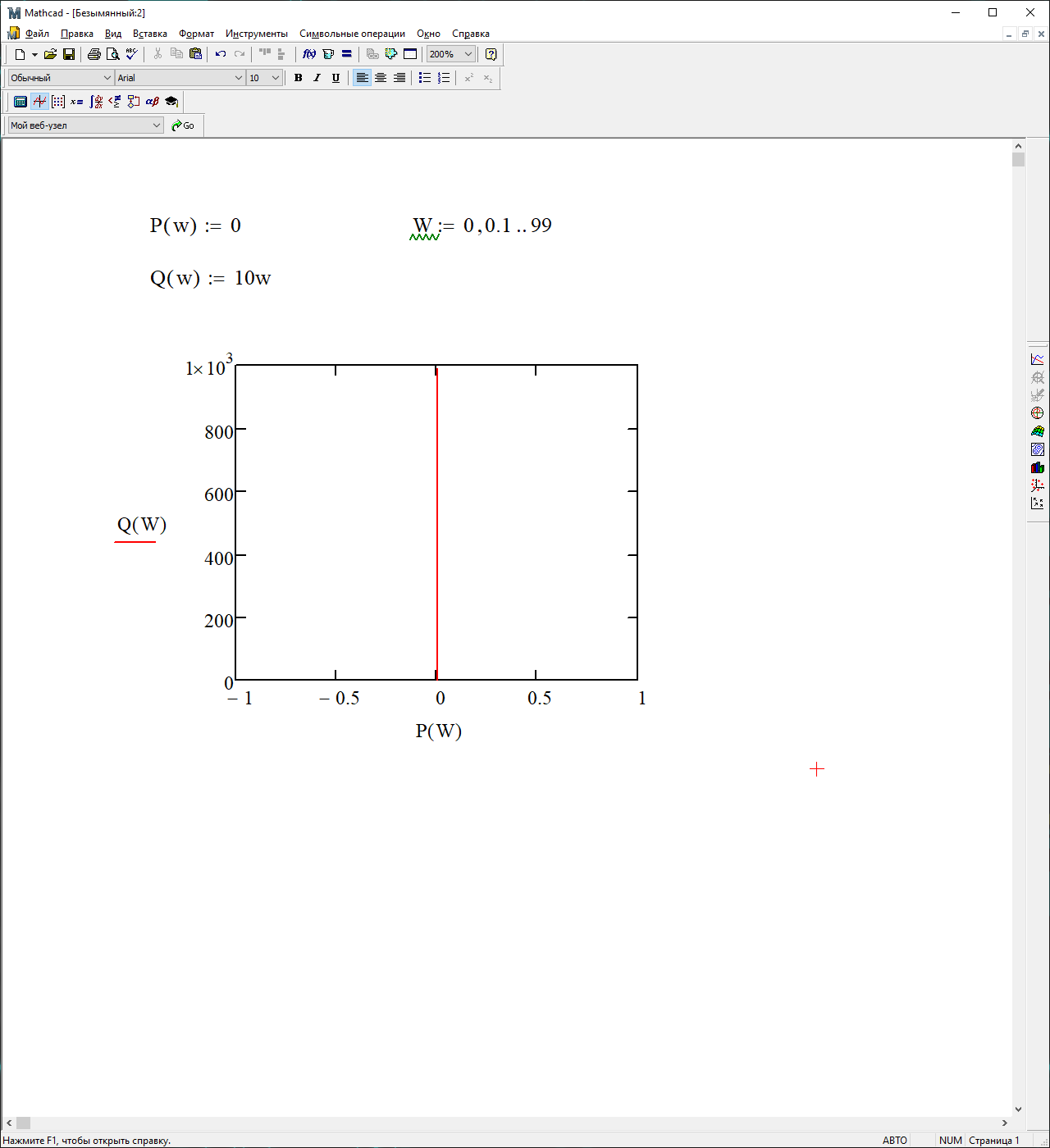
Рисунок 42 – График АФЧХ
3.8. Дифференцирующее звено с замедлением
Произведем замену
 , чтобы перейти к операторному уравнению, получим:
, чтобы перейти к операторному уравнению, получим:(0.1p +1)Y(p) =10Rp(p)
Передаточная функция:
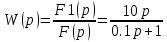
Переходная и весовая функции:
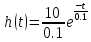
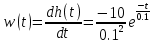
На рисунке 3.43 представлен график весовой функции
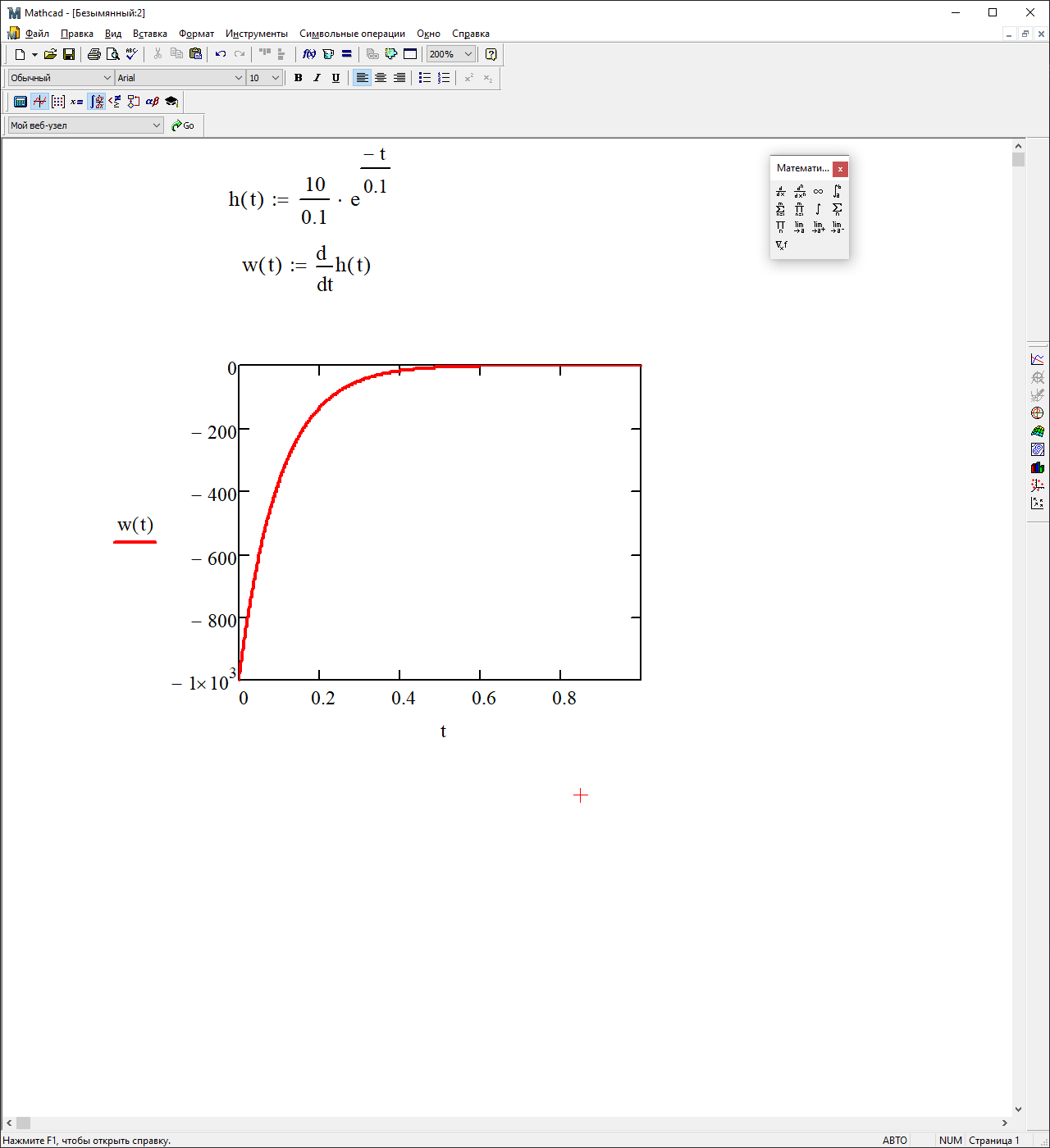
Рисунок 3.43 – График весовой функции
На рисунке 3.44 представлен график переходной характеристики
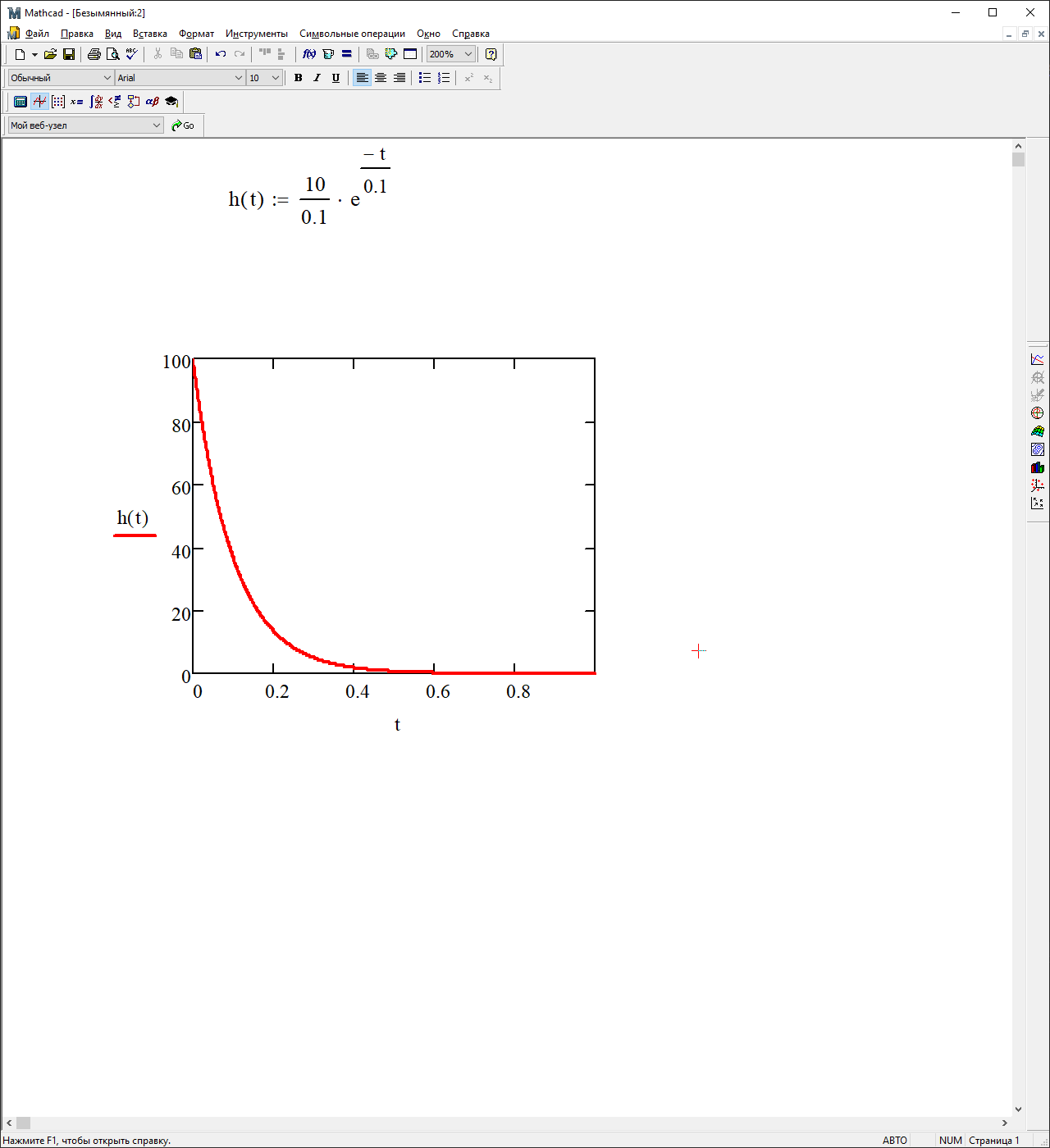
Рисунок 3.44 – График переходной характеристики
Амплитудная частотная характеристика (АЧХ):
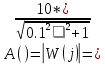
На рисунке 3.45 представлен график АЧХ
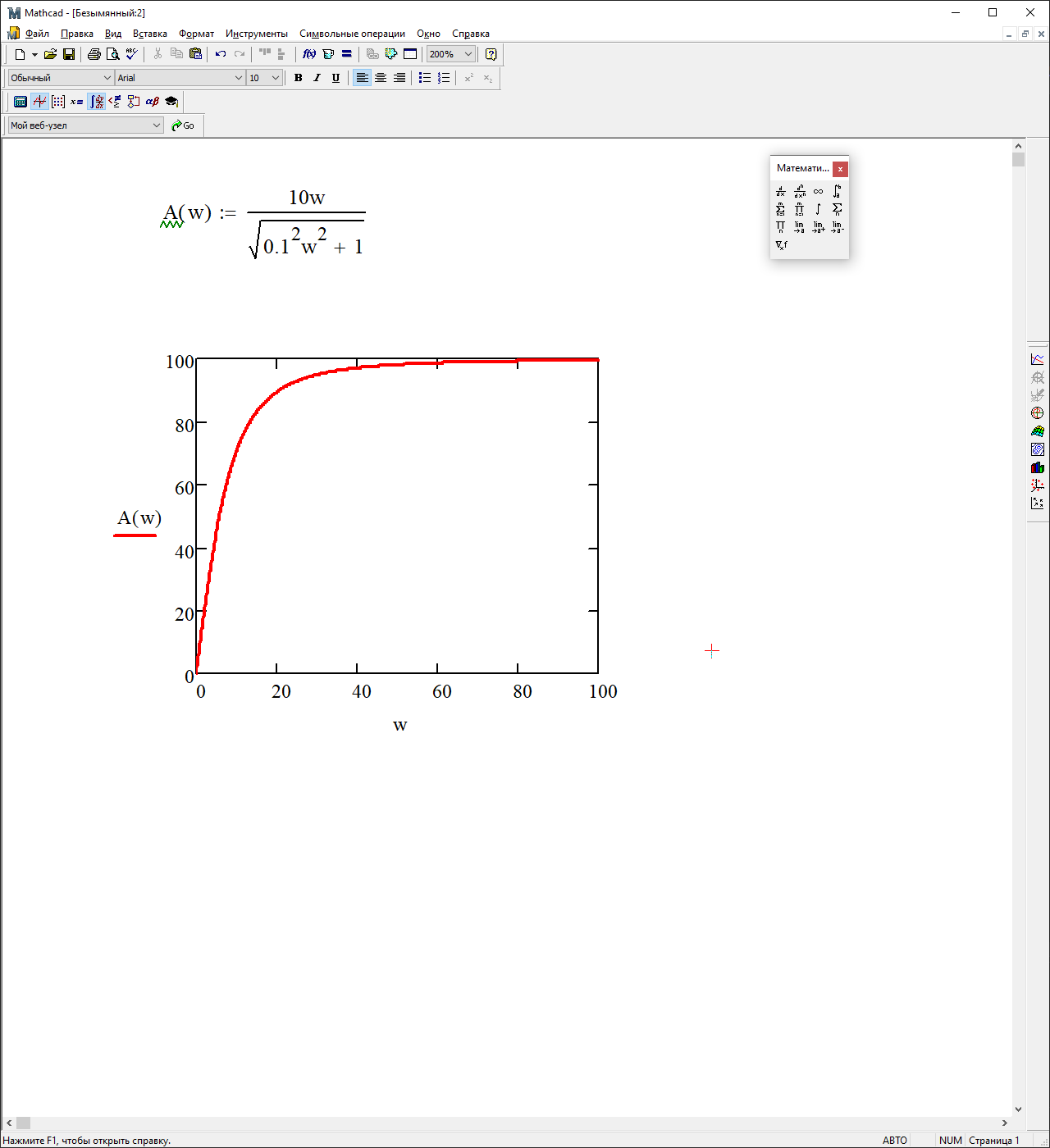
Рисунок 3.45 – График АЧХ
Фазовая частотная характеристика (ФЧХ)
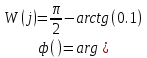
На рисунке 3.46 представлен график ФЧХ
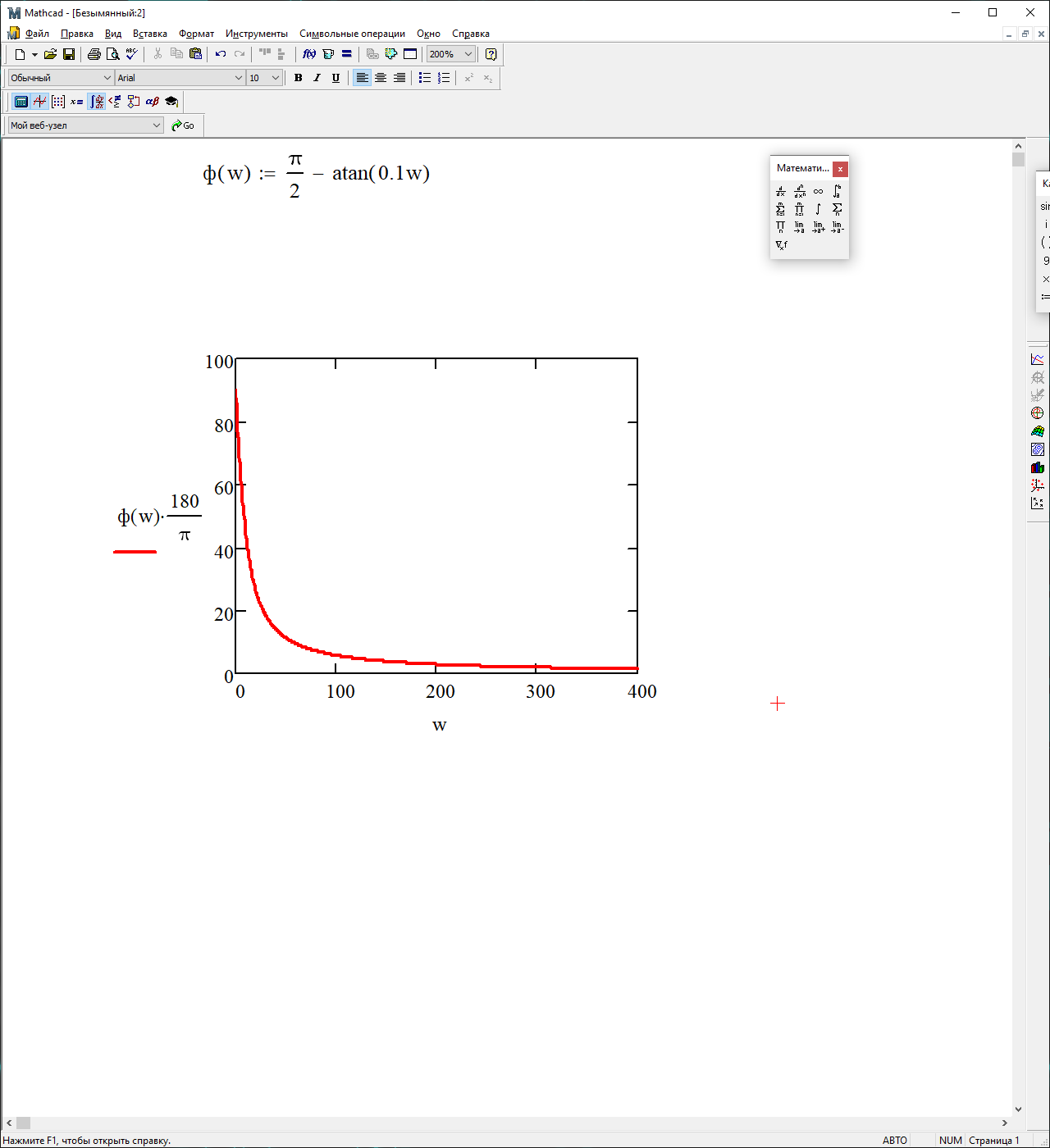
Рисунок 3.46 – График ФЧХ
Логарифмическая амплитудная частотная характеристика (ЛАЧХ):
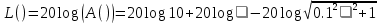
На рисунке 3.47 представлен график ЛАЧХ
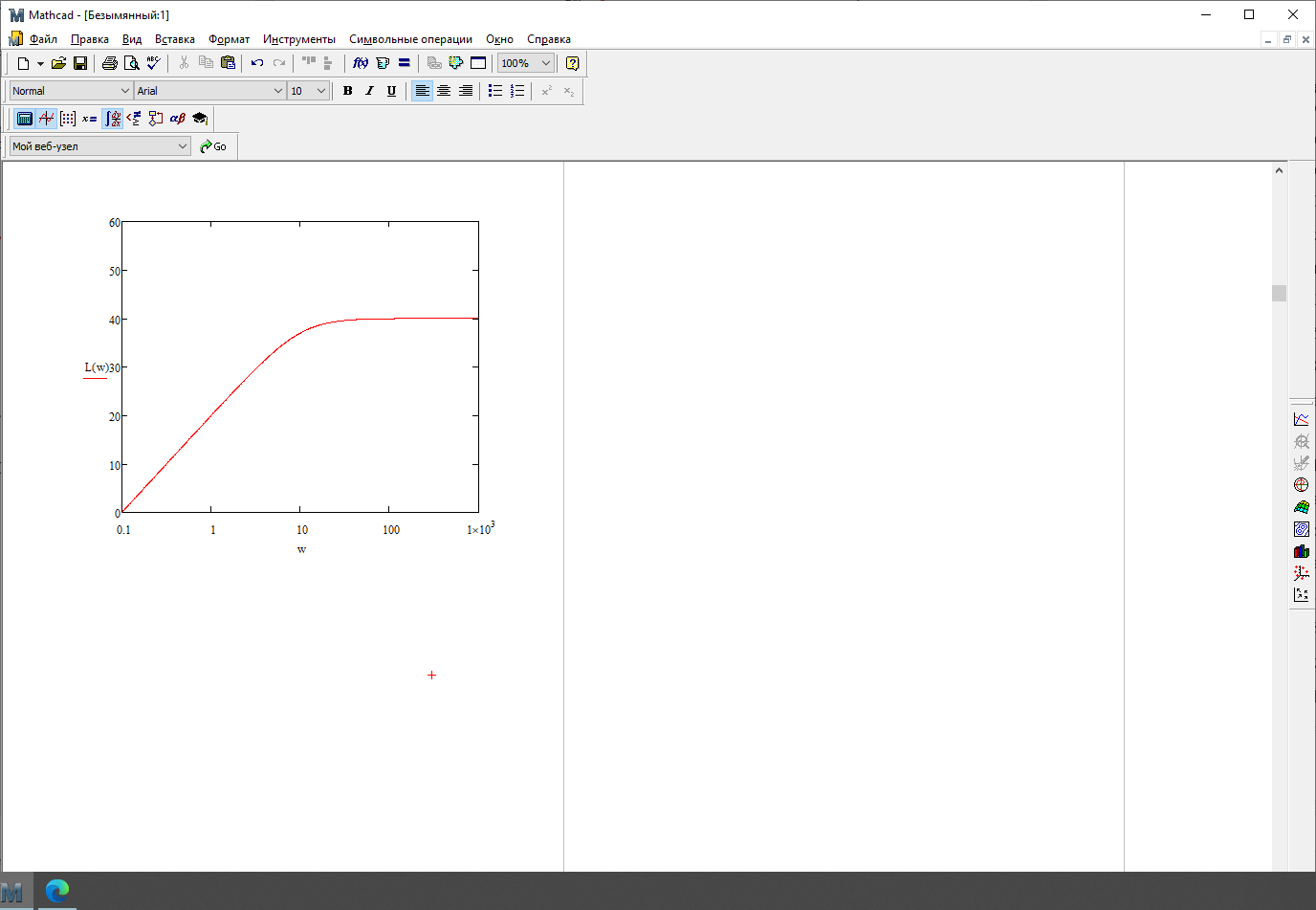
Рисунок 3.47 – График ЛАЧХ
Амплитудно-фазовая частотная характеристика (АФЧХ)
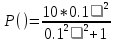
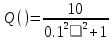
На рисунке 3.48 представлен график АФЧХ
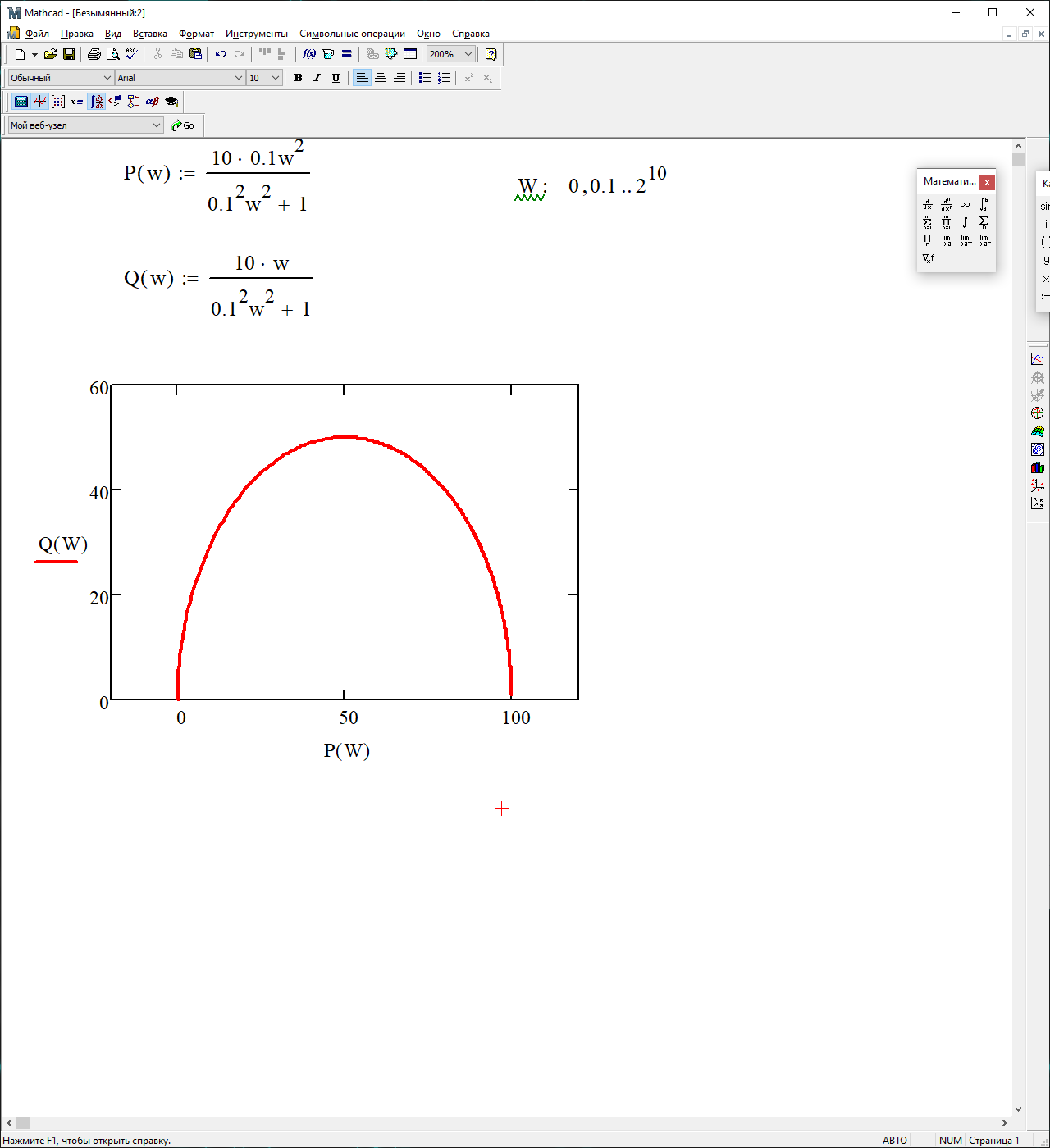
Рисунок 48 – График АФЧХ
4. Частоты сопряжения и среза
Для инерционных звеньев по логарифмическим частотным характеристикам определяем частоты сопряжения и среза.
-
Инерционное 1-го порядка (апериодическое) звено:
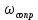 = 10 рад/с;
= 10 рад/с;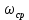 = 99.5 рад/с.
= 99.5 рад/с.Инерционное 2-го порядка (апериодическое) звено:
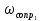 = 12.5 рад/с;
= 12.5 рад/с;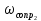 = 50 рад/с;
= 50 рад/с;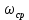 =70.928 рад/с.
=70.928 рад/с.-
Колебательное звено:
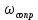 = 5 рад/с;
= 5 рад/с;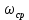 = 16.48 рад/с.
= 16.48 рад/с.-
Идеально интегрирующее звено:
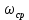 = 10 рад/с;
= 10 рад/с;-
Идеально интегрирующее звено с замедлением:
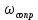 = 0.1 рад/с;
= 0.1 рад/с;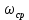 = 7.862 рад/с.
= 7.862 рад/с.-
Идеальное дифференцирующее звено:
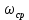 = 0.1 рад/с.
= 0.1 рад/с.-
Дифференцирующее звено с замедление:
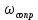 = 10 рад/с;
= 10 рад/с;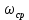 = 0.1 рад/с.
= 0.1 рад/с.5 Заключение
В процессе выполнения лабораторной работы были изучены восемь основных типовых звеньев. При использовании системы Mathcad были построены графики этих звеньев. Также были составлены и решены дифференциальные уравнения для этих типовых звеньев.
Для каждого из звеньев были найдены функции: передаточная, весовая, переходная. Были построены и найдены характеристики: амплитудно-частотная, фазовая частотная и логарифмическая амплитудно-частотная.