Файл: Аппроксимация функции методом наименьших квадратов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.12.2023
Просмотров: 105
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Федеральное государственное бюджетное образовательное учреждение высшего образования
Расчёт с помощью таблиц, выполненных средствами Microsoft Excel.
Программа расчета на языке программирования VBA.
Результаты расчёта на языке программирования VBA.
Результаты, полученные с помощью функции ЛИНЕЙН.
система (3) примет вид:
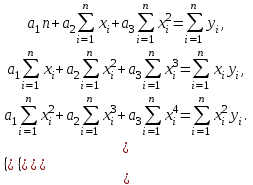 (5)
(5)
В ряде случаев в качестве эмпирической формулы берут функцию, в которую неопределенные коэффициенты входят нелинейно. При этом иногда задачу удается линеаризовать т.е. свести к линейной. К числу таких зависимостей относится экспоненциальная зависимость
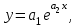 (6) где a1и a2 неопределенные коэффициенты.
(6) где a1и a2 неопределенные коэффициенты.
Линеаризация достигается путем логарифмирования равенства (6), после чего получаем соотношение
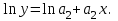 (7)
(7)
Обозначим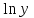 и
и 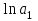 соответственно через
соответственно через 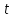 и
и 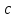 , тогда зависимость (6) может быть записана в виде
, тогда зависимость (6) может быть записана в виде 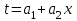 , что позволяет применить формулы (4) с заменой a1 на
, что позволяет применить формулы (4) с заменой a1 на 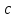 и
и 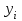 на
на 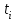 .
.
График восстановленной функциональной зависимости y(x) по результатам измерений (xi, yi), i=1, 2…, n называется кривой регрессии. Для проверки согласия построенной кривой регрессии с результатами эксперимента обычно вводят следующие числовые характеристики: коэффициент корреляции (линейная зависимость), корреляционное отношение и коэффициент детерминированности.
Коэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо в среднем может быть представлена одна из величин в виде линейной функции от другой.
Коэффициент корреляции вычисляется по формуле:
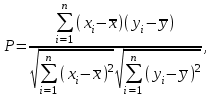 (8)
(8)
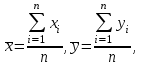 (9)
(9)
где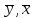 - среднее арифметическое значение соответственно по x, y.
- среднее арифметическое значение соответственно по x, y.
Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе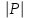
к 1, тем теснее линейная связь между x и y.
В случае нелинейной корреляционной связи условные средние значения располагаются около кривой линии. В этом случае в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация которого не зависит от вида исследуемой зависимости.
Корреляционное отношение вычисляется по формуле:
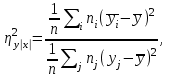 (10)
(10)
где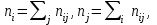 а числитель характеризует рассеяние условных средних около
а числитель характеризует рассеяние условных средних около 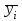 безусловного среднего
безусловного среднего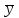 .
.
Всегда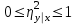 . Равенство
. Равенство 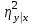 =
=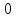 соответствует случайным некоррелированным величинам;
соответствует случайным некоррелированным величинам; 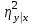 =
=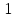 тогда и только тогда, когда имеется точная функциональная связь между xи y. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина
тогда и только тогда, когда имеется точная функциональная связь между xи y. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина 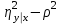 используется в качестве индикатора отклонения регрессии от линейной.
используется в качестве индикатора отклонения регрессии от линейной.
Корреляционное отношение является мерой корреляционной связиyc x в какой угодно форме, но не может дать представления о степени приближенности эмпирических данных к специальной форме. Чтобы выяснить насколько точно построен5ная кривая отражает эмпирические данные вводится еще одна характеристика - коэффициент детерминированности.
Коэффициент детерминированности определяется по формуле:
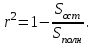 (11)
(11)
где Sост =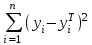 - остаточная сумма квадратов, характеризующая отклонение экспериментальных данных от теоретических.
- остаточная сумма квадратов, характеризующая отклонение экспериментальных данных от теоретических.
Sполн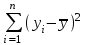
- полная сумма квадратов, где среднее значение yi.
среднее значение yi.
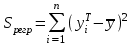 - регрессионная сумма квадратов, характеризующая разброс данных.
- регрессионная сумма квадратов, характеризующая разброс данных.
Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y.
Коэффициент детерминированности всегда не превосходит корреляционное отношение. В случае, когда выполняется равенство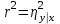 то можно считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные.
то можно считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные.
Для проведения расчётов данные целесообразно расположить в виде таблицы 2, используя средства табличного процессора Microsoft Excel.
Таблица 2.
Пояснение к таблице 2.
Шаг 1.В ячейки А1:A25 заносим значения xi.
Шаг 2.В ячейки B1:B25 заносим значения уi.
Шаг 3.В ячейку С1 вводим формулу=А1^2.
Шаг 4.В ячейки С1:С25 эта формула копируется.
Шаг 5.В ячейку D1 вводим формулу=А1*B1.
Шаг 6.В ячейки D1:D25 эта формула копируется.
Шаг 7.В ячейку F1 вводим формулу=А1^4.
Шаг 8.В ячейки F1:F25 эта формула копируется.
Шаг 9.В ячейку G1 вводим формулу=А1^2*B1.
Шаг 10.В ячейки G1:G25 эта формула копируется.
Шаг 11.В ячейку H1 вводим формулу=LN(B1).
Шаг 12.В ячейки H1:H25 эта формула копируется.
Шаг 13.В ячейку I1 вводим формулу=А1*LN(B1).
Шаг 14.В ячейки I1:I25 эта формула копируется.
Последующие шаги делаем с помощью авто суммирования .
Шаг 15. В ячейку А26 вводим формулу=СУММ(А1:А25).
Шаг 16. В ячейку В26 вводим формулу=СУММ(В1:В25).
Шаг 17. В ячейку С26 вводим формулу=СУММ(С1:С25).
Шаг 18. В ячейку D26 вводим формулу=СУММ(D1:D25).
Шаг 19. В ячейку E26 вводим формулу=СУММ(E1:E25).
Шаг 20. В ячейку F26 вводим формулу=СУММ(F1:F25).
Шаг 21. В ячейку G26 вводим формулу=СУММ(G1:G25).
Шаг 22. В ячейку H26 вводим формулу=СУММ(H1:H25).
Шаг 23. В ячейку I26 вводим формулу =СУММ(I1:I25).
Аппроксимируем функцию линейной функцией
линейной функцией 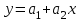 . Для определения коэффициентов
. Для определения коэффициентов 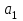 и
и 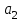 воспользуемся системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 и D26, запишем систему (4) в виде
воспользуемся системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 и D26, запишем систему (4) в виде
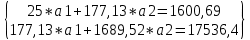 (11)
(11)
решив которую, получим a1 = -36,9917 и a2 = 14,2578
Систему решали методом Крамера. Суть которого состоит в следующем. Рассмотрим систему n алгебраических линейных уравнений с n неизвестными:

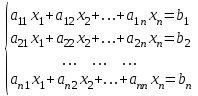 (12)
(12)
Определителем системы называется определитель матрицы системы:
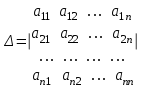 (13)
(13)
Обозначим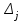 - определитель, который получится из определителя системы Δ заменой j-го столбца на столбец
- определитель, который получится из определителя системы Δ заменой j-го столбца на столбец
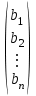 (14)
(14)
Таким образом, линейная аппроксимация имеет вид
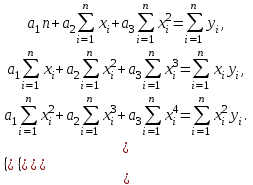 (5)
(5) В ряде случаев в качестве эмпирической формулы берут функцию, в которую неопределенные коэффициенты входят нелинейно. При этом иногда задачу удается линеаризовать т.е. свести к линейной. К числу таких зависимостей относится экспоненциальная зависимость
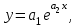 (6) где a1и a2 неопределенные коэффициенты.
(6) где a1и a2 неопределенные коэффициенты.Линеаризация достигается путем логарифмирования равенства (6), после чего получаем соотношение
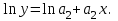 (7)
(7) Обозначим
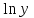 и
и 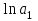 соответственно через
соответственно через 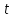 и
и 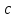 , тогда зависимость (6) может быть записана в виде
, тогда зависимость (6) может быть записана в виде 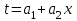 , что позволяет применить формулы (4) с заменой a1 на
, что позволяет применить формулы (4) с заменой a1 на 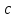 и
и 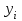 на
на 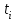 .
.График восстановленной функциональной зависимости y(x) по результатам измерений (xi, yi), i=1, 2…, n называется кривой регрессии. Для проверки согласия построенной кривой регрессии с результатами эксперимента обычно вводят следующие числовые характеристики: коэффициент корреляции (линейная зависимость), корреляционное отношение и коэффициент детерминированности.
Коэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо в среднем может быть представлена одна из величин в виде линейной функции от другой.
Коэффициент корреляции вычисляется по формуле:
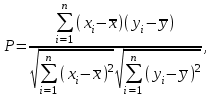 (8)
(8)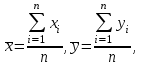 (9)
(9)где
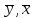 - среднее арифметическое значение соответственно по x, y.
- среднее арифметическое значение соответственно по x, y.Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе
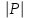
к 1, тем теснее линейная связь между x и y.
В случае нелинейной корреляционной связи условные средние значения располагаются около кривой линии. В этом случае в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация которого не зависит от вида исследуемой зависимости.
Корреляционное отношение вычисляется по формуле:
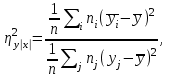 (10)
(10) где
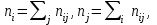 а числитель характеризует рассеяние условных средних около
а числитель характеризует рассеяние условных средних около 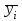 безусловного среднего
безусловного среднего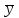 .
.Всегда
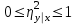 . Равенство
. Равенство 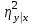 =
=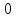 соответствует случайным некоррелированным величинам;
соответствует случайным некоррелированным величинам; 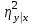 =
=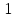 тогда и только тогда, когда имеется точная функциональная связь между xи y. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина
тогда и только тогда, когда имеется точная функциональная связь между xи y. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина 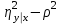 используется в качестве индикатора отклонения регрессии от линейной.
используется в качестве индикатора отклонения регрессии от линейной.Корреляционное отношение является мерой корреляционной связиyc x в какой угодно форме, но не может дать представления о степени приближенности эмпирических данных к специальной форме. Чтобы выяснить насколько точно построен5ная кривая отражает эмпирические данные вводится еще одна характеристика - коэффициент детерминированности.
Коэффициент детерминированности определяется по формуле:
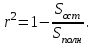 (11)
(11) где Sост =
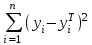 - остаточная сумма квадратов, характеризующая отклонение экспериментальных данных от теоретических.
- остаточная сумма квадратов, характеризующая отклонение экспериментальных данных от теоретических.Sполн
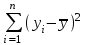
- полная сумма квадратов, где
 среднее значение yi.
среднее значение yi.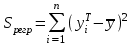 - регрессионная сумма квадратов, характеризующая разброс данных.
- регрессионная сумма квадратов, характеризующая разброс данных.Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y.
Коэффициент детерминированности всегда не превосходит корреляционное отношение. В случае, когда выполняется равенство
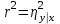 то можно считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные.
то можно считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные.Расчёт с помощью таблиц, выполненных средствами Microsoft Excel.
Для проведения расчётов данные целесообразно расположить в виде таблицы 2, используя средства табличного процессора Microsoft Excel.
| 0,77 | 0,56 | 0,5929 | 0,4312 | 0,456533 | 0,35153 | 0,332024 | -0,57982 | -0,44646 |
| 1,45 | 2,08 | 2,1025 | 3,016 | 3,048625 | 4,420506 | 4,3732 | 0,732368 | 1,061933 |
| 1,76 | 3,04 | 3,0976 | 5,3504 | 5,451776 | 9,595126 | 9,416704 | 1,111858 | 1,956869 |
| 2,23 | 2,76 | 4,9729 | 6,1548 | 11,08957 | 24,72973 | 13,7252 | 1,015231 | 2,263964 |
| 2,65 | 3,65 | 7,0225 | 9,6725 | 18,60963 | 49,31551 | 25,63213 | 1,294727 | 3,431027 |
| 2,76 | 7,06 | 7,6176 | 19,4856 | 21,02458 | 58,02783 | 53,78026 | 1,954445 | 5,394268 |
| 3,45 | 14,98 | 11,9025 | 51,681 | 41,06363 | 141,6695 | 178,2995 | 2,706716 | 9,33817 |
| 3,89 | 15,98 | 15,1321 | 62,1622 | 58,86387 | 228,9805 | 241,811 | 2,771338 | 10,7805 |
| 4,87 | 23,22 | 23,7169 | 113,0814 | 115,5013 | 562,4913 | 550,7064 | 3,145014 | 15,31622 |
| 5,04 | 26,12 | 25,4016 | 131,6448 | 128,0241 | 645,2413 | 663,4898 | 3,262701 | 16,44401 |
| 5,54 | 28,76 | 30,6916 | 159,3304 | 170,0315 | 941,9743 | 882,6904 | 3,358986 | 18,60878 |
| 5,81 | 30,76 | 33,7561 | 178,7156 | 196,1229 | 1139,474 | 1038,338 | 3,426215 | 19,90631 |
| 6,98 | 45,76 | 48,7204 | 319,4048 | 340,0684 | 2373,677 | 2229,446 | 3,82341 | 26,6874 |
| 7,34 | 50,87 | 53,8756 | 373,3858 | 395,4469 | 2902,58 | 2740,652 | 3,929273 | 28,84087 |
| 7,86 | 60,45 | 61,7796 | 475,137 | 485,5877 | 3816,719 | 3734,577 | 4,101817 | 32,24028 |
| 8,12 | 65,87 | 65,9344 | 534,8644 | 535,3873 | 4347,345 | 4343,099 | 4,187683 | 34,00399 |
| 8,87 | 77,85 | 78,6769 | 690,5295 | 697,8641 | 6190,055 | 6124,997 | 4,354784 | 38,62693 |
| 9,45 | 86,09 | 89,3025 | 813,5505 | 843,9086 | 7974,937 | 7688,052 | 4,455393 | 42,10347 |
| 10,87 | 101,65 | 118,1569 | 1104,936 | 1284,366 | 13961,05 | 12010,65 | 4,621536 | 50,23609 |
| 11,23 | 124,37 | 126,1129 | 1396,675 | 1416,248 | 15904,46 | 15684,66 | 4,823261 | 54,16522 |
| 11,89 | 130,75 | 141,3721 | 1554,618 | 1680,914 | 19986,07 | 18484,4 | 4,873287 | 57,94338 |
| 12,56 | 149,56 | 157,7536 | 1878,474 | 1981,385 | 24886,2 | 23593,63 | 5,007698 | 62,89668 |
| 13,43 | 172,45 | 180,3649 | 2316,004 | 2422,301 | 32531,5 | 31103,93 | 5,150107 | 69,16594 |
| 13,55 | 175,51 | 183,6025 | 2378,161 | 2487,814 | 33709,88 | 32224,07 | 5,167696 | 70,02228 |
| 14,76 | 200,54 | 217,8576 | 2959,97 | 3215,578 | 47461,93 | 43689,16 | 5,301014 | 78,24296 |
| 177,13 | 1600,69 | 1689,517 | 17536,43 | 18556,16 | 219852,7 | 207313,9 | 83,99674 | 749,2311 |
| x | y | x^2 | x*y | x^3 | x^4 | (x^2)*y | lny | x*lny |
Таблица 2.
Пояснение к таблице 2.
Шаг 1.В ячейки А1:A25 заносим значения xi.
Шаг 2.В ячейки B1:B25 заносим значения уi.
Шаг 3.В ячейку С1 вводим формулу=А1^2.
Шаг 4.В ячейки С1:С25 эта формула копируется.
Шаг 5.В ячейку D1 вводим формулу=А1*B1.
Шаг 6.В ячейки D1:D25 эта формула копируется.
Шаг 7.В ячейку F1 вводим формулу=А1^4.
Шаг 8.В ячейки F1:F25 эта формула копируется.
Шаг 9.В ячейку G1 вводим формулу=А1^2*B1.
Шаг 10.В ячейки G1:G25 эта формула копируется.
Шаг 11.В ячейку H1 вводим формулу=LN(B1).
Шаг 12.В ячейки H1:H25 эта формула копируется.
Шаг 13.В ячейку I1 вводим формулу=А1*LN(B1).
Шаг 14.В ячейки I1:I25 эта формула копируется.
Последующие шаги делаем с помощью авто суммирования .
Шаг 15. В ячейку А26 вводим формулу=СУММ(А1:А25).
Шаг 16. В ячейку В26 вводим формулу=СУММ(В1:В25).
Шаг 17. В ячейку С26 вводим формулу=СУММ(С1:С25).
Шаг 18. В ячейку D26 вводим формулу=СУММ(D1:D25).
Шаг 19. В ячейку E26 вводим формулу=СУММ(E1:E25).
Шаг 20. В ячейку F26 вводим формулу=СУММ(F1:F25).
Шаг 21. В ячейку G26 вводим формулу=СУММ(G1:G25).
Шаг 22. В ячейку H26 вводим формулу=СУММ(H1:H25).
Шаг 23. В ячейку I26 вводим формулу =СУММ(I1:I25).
Аппроксимируем функцию
 линейной функцией
линейной функцией 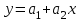 . Для определения коэффициентов
. Для определения коэффициентов 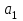 и
и 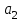 воспользуемся системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 и D26, запишем систему (4) в виде
воспользуемся системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 и D26, запишем систему (4) в виде 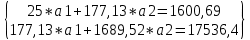 (11)
(11)решив которую, получим a1 = -36,9917 и a2 = 14,2578
Систему решали методом Крамера. Суть которого состоит в следующем. Рассмотрим систему n алгебраических линейных уравнений с n неизвестными:

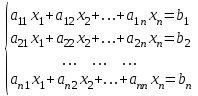 (12)
(12)Определителем системы называется определитель матрицы системы:
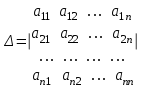 (13)
(13)Обозначим
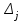 - определитель, который получится из определителя системы Δ заменой j-го столбца на столбец
- определитель, который получится из определителя системы Δ заменой j-го столбца на столбец 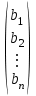 (14)
(14)Таким образом, линейная аппроксимация имеет вид