Файл: Аппроксимация функции методом наименьших квадратов.docx

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Санкт-Петербургский государственный горный Университет»

КУРСОВАЯ РАБОТА

по дисциплине Информатика

^{(наименование учебной дисциплины согласно учебному плану)}

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Тема: Аппроксимация функции методом наименьших квадратов


Автор: студент гр. ЭРБ-22 _______________ / Каримов.А.Ф/

^{(подпись) (Ф.И.О.)}


ОЦЕНКА: _____________
Дата: ___________________
ПРОВЕРИЛ
Руководитель проекта _доцент__ ________________ /_Ильин А.Е./

^{(должность) (подпись) (Ф.И.О.)}

Санкт - Петербург

2023

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ



ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ

УТВЕРЖДАЮ Заведующий кафедрой _________________/Кризский В.Н./ (подпись) (Ф.И.О.) "5" февраля 2023г.

Кафедра информатики и компьютерных технологий

ЗАДАНИЕ НА КУРСОВОЕ ПРОЕКТИРОВАНИЕ
студенту группы ЭРБ-22 Каримов А.Ф ^{(шифр группы) (Ф.И.О.)}
Тема :Аппроксимация экспериментальных данных методом наименьших квадратов

Исходные данные: ________Вариант №4_____________________________________

Содержание пояснительной записки: Пояснительная записка включает в себя задание на выполнение работы; расчетные формулы; таблицы, выполненные средствами Microsoft Excel, с пояснениями; результаты расчета; в виде таблиц и графиков; программа на VBA и результаты ее работы; выводы; библиографический список.

---

_________________________
Требования к графической части проекта и пояснительной записке содержатся в Методических указаниях к выполнению курсовой работы.
Срок сдачи законченной работы 10 мая 2023 г.

Задание выдал: доцент / Ильин А.Е /

^{(должность) (подпись) (Ф.И.О.)}
Задание принял к исполнению студент: / /

^{(подпись) (Ф.И.О.)}

Дата выдачи задания: 15 февраля 2023 г

Аннотация.

Пояснительная записка представляет собой отчёт о выполнении курсовой работы. В ней рассматриваются вопросы построения эмпирических формул методом наименьших квадратов, линейным и экспоненциальным методом (МНК) средствами пакета Microsoft Excel и решение данной задачи в VBA. По окончании выполнения работы необходимо решить, каким методом задача решается лучше всего, а также определить каким средством это легче сделать: посредством Microsoft Excel или VBA.

Страниц- 26, таблиц- 9, изображений- 4.

Оглавление.

Введение.

Целью курсовой работы является углубление знаний по информатике, развитие и закрепление навыков работы с Microsoft Excel и применение их для решения задач с помощью ЭВМ из предметной области, связанной с исследованиями.

В каждом задании формулируются условия задачи, исходные данные, форма выдачи результатов, указываются основные математические зависимости для решения задачи. В соответствии с методом решения задачи разрабатывается алгоритм решения, который представляется в графической форме. Разработанная программа проходит этап отладки, в процессе которого обнаруживаются ошибки, допущенные при составлении алгоритма и написании программы. Контрольный расчет позволяет убедится в правильности работы программы.

---

Постановка задачи.

1. Используя метод наименьших квадратов функцию 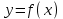, заданную таблично,

аппроксимировать

а) многочленом первой степени ;

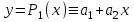б) многочленом второй степени ;

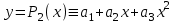в) экспоненциальной зависимостью .

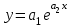2. Для каждой зависимости вычислить коэффициент детерминированности.

3. Вычислить коэффициент корреляции (только в случае а).

4. Для каждой зависимости построить линию тренда.

5. Используя функцию ЛИНЕЙН вычислить числовые характеристики зависимости 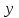от .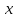

6. Сравнить свои вычисления с результатами, полученными при помощи функции ЛИНЕЙН.

7. Сделать вывод, какая из полученных формул наилучшим образом аппроксимирует функцию .

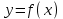8. Написать программу на одном из языков программирования и сравнить результаты счета с полученными выше.

Вариант 1. Функция 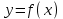задана табл. 1

Таблица 1.

0,77	0,56
1,45	2,08
1,76	3,04
2,23	2,76
2,65	3,65
2,76	7,06
3,45	14,98
3,89	15,98
4,87	23,22
5,04	26,12
5,54	28,76
5,81	30,76
6,98	45,76
7,34	50,87
7,86	60,45
8,12	65,87
8,87	77,85
9,45	86,09
10,87	101,65
11,23	124,37
11,89	130,75
12,56	149,56
13,43	172,45
13,55	175,51
14,76	200,54
177,13	1600,69
x	y

---

---

Расчётные формулы.

Часто при анализе эмпирических данных возникает необходимость найти функциональную зависимость между величинами x и y, которые получены в результате опыта или измерений.

Х_i (независимая величина) задается экспериментатором, а y_i, называемая эмпирическими или опытными значениями получается в результате опыта.

Аналитический вид функциональной зависимости, существующей между величинами x и y обычно неизвестен, поэтому возникает практически важная задача - найти эмпирическую формулу

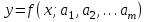, (1)

(где 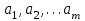- параметры), значения которой при 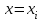возможно мало отличались бы от опытных значений .

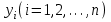Согласно методу наименьших квадратов наилучшими коэффициентами 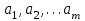считаются те, для которых сумма квадратов отклонений найденной эмпирической функции от заданных значений функции

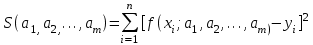(2)

будет минимальной.

Используя необходимое условие экстремума функции нескольких переменных – равенство нулю частных производных, находят набор коэффициентов 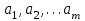, которые доставляют минимум функции 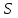, определяемой формулой (2) и получают нормальную систему для определения коэффициентов :

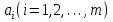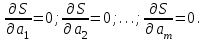(3)

Таким образом, нахождение коэффициентов 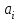сводится к решению системы (3).

Вид системы (3) зависит от того, из какого класса эмпирических формул мы ищем зависимость (1). В случае линейной зависимости система (3) примет вид:

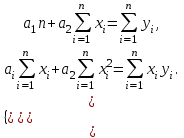
(4)

В случае квадратичной зависимости

---