Файл: Аппроксимация функции методом наименьших квадратов.docx

y = 14,258x-36,992 (15)
Решение системы (11) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 3.

Таблица 3.

25	177,13	1600,69
177,13	1689,517	17536,43
Обратная матрица				a1=		-36,9917
0,155531186	-0,01631			a2=	14,25779
-0,016305988	0,002301

В таблице 3 в ячейках A32:B33 записана формула {=МОБР(А28:В29)}.

В ячейках Е32:Е33 записана формула {=МУМНОЖ(А32:В33),(C28:С29)}.

Далее аппроксимируем функцию квадратичной функцией 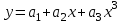. Для определения коэффициентов a₁, a₂ и a₃ воспользуемся системой (5). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 , D26, E26, F26, G26 запишем систему (5) в виде

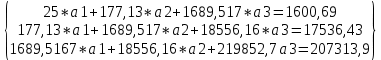(16)
решив которую, получим a1 = -1,39325, a2 = 0,70294 и a3 = 0,894344

Таким образом, квадратичная аппроксимация имеет вид

y =0,8943x^2+0,7029x-1,3933 (17)

Решение системы (16) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 4.

Таблица 4.

25	177,13	1689,517	1600,69
177,13	1689,517	18556,16	17536,43
1689,5167	18556,16	219852,7	207313,9
Обратная матрица
0,425826829	-0,11923	0,006791		a1=	-1,39325
-0,119226748	0,041491	-0,00259		a2=	0,70294
0,006790678	-0,00259	0,000171		a3=	0,894344

---

В таблице 4 в ячейках А41:С43 записана формула {=МОБР(А35:С37)}.

В ячейках F41:F43 записана формула {=МУМНОЖ(А41:C43),(D36:D38)}.

Теперь аппроксимируем функцию экспоненциальной функцией 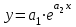. Для определения коэффициентов и прологарифмируем значения и, используя итоговые суммы таблицы 2, расположенные в ячейках A26, C26, H26 и I26, получим систему

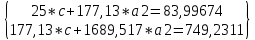(18)

где .

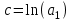Решив систему (18), получим c = 0,847159 и a2 = 0,354642.

После потенцирования получим a1 = 2,33301.

Таким образом, экспоненциальная аппроксимация имеет вид

y = 2,333e^0,3546x (19)

Решение системы (18) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 5.

Таблица 5.

25	177,13	83,99674
177,13	1689,517	749,2311
Обратная матрица				c		0,847159
0,155531186	-0,01631			a2	0,354642
-0,016305988	0,002301			a1	2,33301

В таблице 5 в ячейках А50:A51 записана формула {=МОБР(А46:B47)}.

---

В ячейках Е49:Е50 записана формула {=МУМНОЖ(A50:B51;C46:C47)}

В ячейке Е51 записана формула=EXP(E49).
Вычислим среднее арифметическое 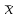и 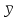по формулам:
; .
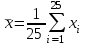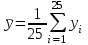Результаты расчета 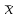и 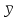средствами Microsoft Excel представлены в таблице 6.
Таблица 6.

Хср.=	7,0852
Yср.=	64,0276

В ячейке В54 записана формула=А26/25.

В ячейке В55 записана формула=В26/25
Для того, чтобы рассчитать коэффициент корреляции и коэффициент детерминированности данные целесообразно расположить в виде таблицы 7, которая является продолжением таблицы 2.

0,77	0,56	400,8106	39,88175	4028,136	706,1335	0,777451	6,277881
1,45	2,08	349,0871	31,75548	3837,505	338,4819	0,329052	3,318276
1,76	3,04	324,7712	28,35776	3719,487	223,1428	0,181269	1,729278
2,23	2,76	297,4665	23,57297	3753,719	63,31073	3,466255	5,687874
2,65	3,65	267,7867	19,671	3645,455	8,171216	9,610439	5,388325
2,76	7,06	246,3963	18,70736	3245,307	22,09167	0,089771	0,724502
3,45	14,98	178,2978	13,21468	2405,667	7,74122	10,91098	49,7001
3,89	15,98	153,5217	10,2093	2308,572	6,205685	1,222152	45,03236
4,87	23,22	90,397	4,907111	1665,26	85,0776	0,000447	101,9759
5,04	26,12	77,52862	4,182843	1436,986	76,52008	1,569158	148,4227
5,54	28,76	54,4955	2,387643	1243,804	175,2041	1,41584	146,8673
5,81	30,76	42,42284	1,626135	1106,733	227,5895	4,496107	154,9193
6,98	45,76	1,921752	0,011067	333,7052	281,1551	1,758483	325,0346
7,34	50,87	-3,35256	0,064923	173,1224	281,9204	1,165666	374,8982
7,86	60,45	-2,77192	0,600315	12,79922	213,877	1,136173	509,0236
8,12	65,87	1,906516	1,070811	3,394438	166,7083	6,694268	591,5519
8,87	77,85	24,67022	3,185511	191,0587	135,1382	6,990427	558,928
9,45	86,09	52,17316	5,592279	486,7495	135,8253	0,947297	380,3205
10,87	101,65	142,3933	14,32471	1415,445	267,0109	105,4862	72,76785
11,23	124,37	250,1072	17,17937	3641,205	1,554329	25,81543	0,663738
11,89	130,75	320,5878	23,0861	4451,879	3,180557	7,022657	753,4505
12,56	149,56	468,2728	29,97344	7315,791	55,85876	1,078067	2608,183
13,43	172,45	687,9184	40,25649	11755,42	322,5471	9,575656	10139,49
13,55	175,51	720,7114	41,79364	12428,33	372,8245	10,07792	11992,48
14,76	200,54	1047,705	58,90256	18635,64	733,6916	10,77045	56274,61
177,13	1600,69	6195,225	434,5152	93241,16	4910,962	222,5877	85251,45
x	y	(x-xср)*(y-yср)	(x-xср)^2	(y-yср)^2	линейн.	квадр.	экспон.

---

Таблица 7.
Пояснение к таблице 7.

Ячейки А1:А26 и В1:В26 уже заполнены .

Далее делаем следующие шаги.

Шаг 1.В ячейку J1 вводим формулу=(A1-$B$54)*(B1-$B$55).

Шаг 2.В ячейки J2:J25 эта формула копируется.

Шаг 3.В ячейку K1 вводим формулу=(A1-$B$54)^2.

Шаг 4.В ячейки k2:K25 эта формула копируется.

Шаг 5.В ячейку L1 вводим формулу=(B1-$B$55)^2.

Шаг 6.В ячейки L2:L25 эта формула копируется.

Шаг 7.В ячейку M1 вводим формулу=($F$32+$F$33*A1-B1)^2.

Шаг 8.В ячейки M2:M25 эта формула копируется.

Шаг 9.В ячейку N1 вводим формулу=($F$41+$F$42*A1+$F$43*A1^2-B1)^2.

Шаг 10.В ячейки N2:N25 эта формула копируется.

Шаг 11.В ячейку O1 вводим формулу=($F$51*EXP($F$50*A1)-B1)^2.

Шаг 12.В ячейки O2:O25 эта формула копируется.

Последующие шаги делаем с помощью авто суммирования .

Шаг 13.В ячейку J26 вводим формулу =CУММ(J1:J25).

Шаг 14.В ячейку K26 вводим формулу =CУММ(K1:K25).

Шаг 15.В ячейку L26 вводим формулу =CУММ(L1:L25).

Шаг 16.В ячейку M26 вводим формулу =CУММ(M1:M25).

Шаг 17.В ячейку N26 вводим формулу =CУММ(N1:N25).

Шаг 18.В ячейку O26 вводим формулу =CУММ(O1:O25).

Теперь проведем расчеты коэффициента корреляции по формуле (8) (только для линейной аппроксимации) и коэффициента детерминированности по формуле (10). Результаты расчетов средствами Microsoft Excel представлены в таблице 8.

Коэффициент корреляции	0,973309
Коэффициент детерминированности (линейная аппроксимация)	0,947331
Коэффициент детерминированности (квадратичная аппроксимация)	0,997613
Коэффициент детерминированности (экспоненциальная аппроксимация)	0,085689

Таблица 8.
В ячейке B57 записана формула=J26/(K26*L26) ^ (1/2).

В ячейке B58 записана формула=1-M26/L26.

В ячейке B59 записана формула=1-N26/L26.

В ячейке B60 записана формула=1-O26/L26.

Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные.

---

Схема алгоритма.

Начало



Ввод данных



Промежуточные расчёты (согл. таблице 2)


Аппроксимируем функцию y=f(x) линейной функцией (находим коэффициенты а₁ и а₂)



Аппроксимируем функцию y=f(x) квадратичной функцией 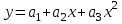(находим коэффициенты а₁, а₂ и а₃)




Аппроксимируем функцию y=f(x) экспоненциальной функцией (находим коэффициенты а₁ и а₂)




Находим среднее арифметическое и



Промежуточные расчёты (согл. таблице 7)



Находим коэффициент корреляции r

(для линейной аппроксимации)




Находим коэффициент детерминированности r²

для линейной, квадратичной и экспоненциальной аппроксимации



Вывод результатов



Конец


Рис.1. Схема алгоритма для программы расчёта.

Программа расчета на языке программирования VBA.

Sub prog()

For i = 1 To 25

Cells(i, 23) = Cells(i, 1) ^ 2

Cells(i, 24) = Cells(i, 1) * Cells(i, 2)

Cells(i, 25) = Cells(i, 1) ^ 3

Cells(i, 26) = Cells(i, 1) ^ 4

Cells(i, 27) = Cells(i, 1) ^ 2 * Cells(i, 2)

Cells(i, 28) = Log(Cells(i, 2))

Cells(i, 29) = Log(Cells(i, 2)) * Cells(i, 1)

Cells(i, 30) = (summirovanie(1) / 25 - Cells(i, 1)) * (summirovanie(2) / 25 - Cells(i, 2))

Cells(i, 31) = (Cells(i, 1) - summirovanie(1) / 25) ^ 2

Cells(i, 32) = (Cells(i, 2) - summirovanie(2) / 25) ^ 2

Next

Dim y3(1, 0) As Variant

y1 = krameffor2(25, summirovanie(1), summirovanie(1), summirovanie(23), summirovanie(2), summirovanie(24))

с = krameffor2(25, summirovanie(1), summirovanie(1), summirovanie(23), summirovanie(28), summirovanie(29))

y3(0, 0) = exp(с(0, 0))

y3(1, 0) = с(1, 0)

y2 = krameffor3(25, summirovanie(1), summirovanie(23), summirovanie(1), summirovanie(23), summirovanie(25), summirovanie(23), summirovanie(25), summirovanie(26), summirovanie(2), summirovanie(24), summirovanie(27))

For i = 1 To 25

Cells(i, 33) = (y1(0, 0) + y1(1, 0) * Cells(i, 1) - Cells(i, 2)) ^ 2

Cells(i, 34) = (y2(0, 0) + y2(1, 0) * Cells(i, 1) + y2(2, 0) * Cells(i, 1) ^ 2 - Cells(i, 2)) ^ 2

Cells(i, 35) = (y3(0, 0) * exp(y3(1, 0) * Cells(i, 1)) - Cells(i, 2)) ^ 2

Next

koef1 = summirovanie(30) / (summirovanie(31) * summirovanie(32)) ^ (1 / 2)

koef2 = 1 - summirovanie(33) / summirovanie(32)

koef3 = 1 - summirovanie(34) / summirovanie(32)

koef4 = 1 - summirovanie(35) / summirovanie(32)

---