Файл: Аппроксимация функции методом наименьших квадратов.docx

MsgBox ("Линейный" + vbNewLine + "a1=" + Str(Round(y1(0, 0), 5)) + vbNewLine + "a2=" + Str(Round(y1(1, 0), 5)))

MsgBox ("Квадратичный" + vbNewLine + "a1=" + Str(Round(y2(0, 0), 5)) + vbNewLine + "a2=" + Str(Round(y2(1, 0), 5)) + vbNewLine + "a3=" + Str(Round(y2(2, 0), 5)))

MsgBox ("Экспонентальный" + vbNewLine + "a1=" + Str(Round(y3(0, 0), 5)) + vbNewLine + "a2=" + Str(Round(y3(1, 0), 5)))

MsgBox ("Коэффициенты" + vbNewLine + "коэффициент корреляции=" + Str(Round(koef1, 5)) + vbNewLine + "коэффициент д.линейный=" + Str(Round(koef2, 5)) + vbNewLine + "коэффициент д.квадратный=" + Str(Round(koef3, 5)) + vbNewLine + "коэффициент д.экспонентальный=" + Str(Round(koef4, 5)))

End Sub

Function krameffor2(a, b, c, d, e, f)

Dim resh(1, 0) As Variant

opred = a * d - b * c

opred1 = e * d - b * f

opred2 = a * f - e * c

resh(0, 0) = opred1 / opred

resh(1, 0) = opred2 / opred

krameffor2 = resh

End Function

Function krameffor3(a1, a2, a3, b1, b2, b3, c1, c2, c3, e, f, g)

Dim resh(2, 0) As Variant

opred = a1 * b2 * c3 + a2 * b3 * c1 + a3 * b1 * c2 - a3 * b2 * c1 - a1 * b3 * c2 - a2 * b1 * c3

aa1 = e

bb1 = f

cc1 = g

x1 = aa1 * b2 * c3 + a2 * b3 * cc1 + a3 * bb1 * c2 - a3 * b2 * cc1 - aa1 * b3 * c2 - a2 * bb1 * c3

aa2 = e

bb2 = f

cc2 = g

x2 = a1 * bb2 * c3 + aa2 * b3 * c1 + a3 * b1 * cc2 - a3 * bb2 * c1 - a1 * b3 * cc2 - aa2 * b1 * c3

aa3 = e

bb3 = f

cc3 = g

x3 = a1 * b2 * cc3 + a2 * bb3 * c1 + aa3 * b1 * c2 - aa3 * b2 * c1 - a1 * bb3 * c2 - a2 * b1 * cc3

resh(0, 0) = x1 / opred

resh(1, 0) = x2 / opred

resh(2, 0) = x3 / opred

krameffor3 = resh

End Function

Function summirovanie(n)

summirovanie = 0

For i = 1 To 25

summirovanie = summirovanie + Cells(i, n)

Next

End Function

Результаты расчёта на языке программирования VBA.

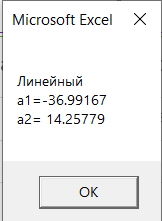
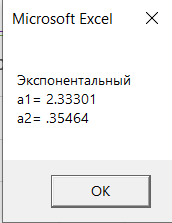
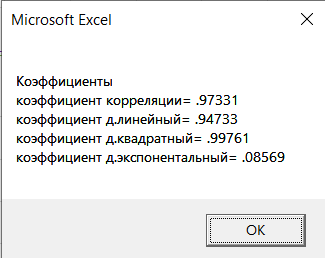
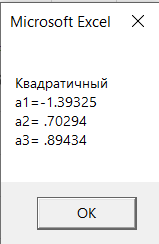
Результаты, полученные с помощью функции ЛИНЕЙН.

Рассмотрим назначение функции ЛИНЕЙН.

Эта функция использует метод наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные.

Функция возвращает массив, который описывает полученную прямую. Уравнение для прямой линии имеет следующий вид:

y = m₁x₁ + m₂x₂ + ... + b или y = mx + b,

где зависимое значение y является функцией независимого значения x. Значения m - это коэффициенты, соответствующие каждой независимой переменной x, а b - это постоянная. Заметим, что y, x и m могут быть векторами.

Для получения результатов необходимо создать табличную формулу

, которая будет занимать 5 строк и 2 столбца. Этот интервал может располагаться в произвольном месте на рабочем листе. В этот интервал требуется ввести функцию ЛИНЕЙН.

В результате должны заполниться все ячейки интервала А66:В70 (как показано в таблице 9).
Таблица 9.

	A	B
66	14,25778631	-36,9917
67	0,070099815	5,762728
68	0,947330534	14,61233
69	431, 6856521	23
70	88330,19721	4910,962

Поясним назначение некоторых величин, расположенных в таблице 9.

Величины, расположенные в ячейках А66 и В66 характеризуют соответственно наклон и сдвиг.

А68 – коэффициент детерминированности.

А69 – F-наблюдаемое значение.

B69 – число степеней свободы.

A70 – регрессионная сумма квадратов.

B70 – остаточная сумма квадратов.

Представление результатов в виде графиков.

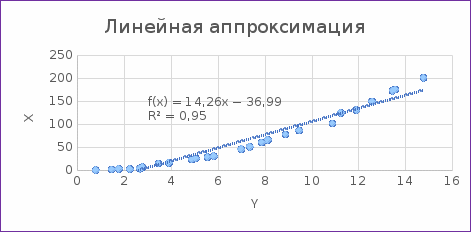
Рис.1. График линейной аппроксимации

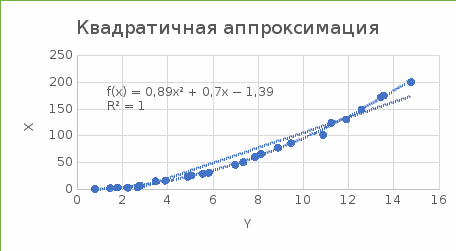
Рис.2. График квадратичной аппроксимации

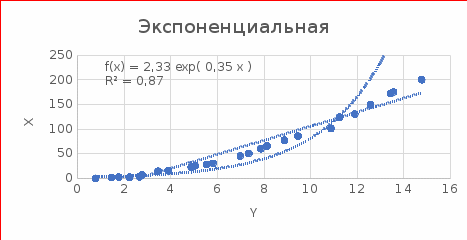
Рис.3. График экспоненциальной аппроксимации

Вывод.

Сделаем вывод по результатам проведенных работ:

Результаты расчетов показывают, что квадратичная аппроксимация лучшим образом описывает экспериментальные данные, потому что линия тренда для неё наиболее точно описывает поведение функции на заданном участке.

Сравнивая результаты, полученные при помощи функции ЛИНЕЙН, видим, что они полностью совпадают с вычислениями, проведенными выше. Это показывает, что вычисления верны.

Результаты, полученные с помощью программы на языке VBA, полностью совпадают со значениями

, полученными в Exсel, что говорит о верности вычислений.

Список используемой литературы.

Методические указания «Аппроксимация экспериментальных данных методом наименьших квадратов».
Руководство по прикладному программированию на VBA: Учебное

пособие / Маланичев И.В., Ермолаева Л.Б.