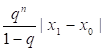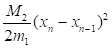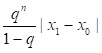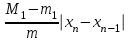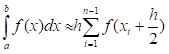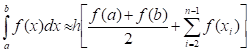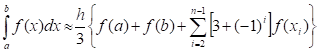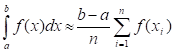1. 
   Құбыр ішіндегі сығылмайтын сұйық ағысының екі өлшемді қалыптасқан температуралық өрісін қай әдіспен есептеген дұрыс?
   

1. 
   қуып өту (прогонка)
   
2. 
   Гаусс
   
3. 
   жәй итерация
   
4. 
   Монте – Карло
   

2. 
   Сөзбен сипаттауды қолдану негізіндегі үлгілеу:
   

1. 
   вербалды
   
2. 
   геометриялық
   
3. 
   физикалық
   
4. 
   ақпараттық
   

3. 
   Формула, теңдік, теңсіздік, сызбақ кейіптемелерімен байланыстырылған сипаттауды қолдану негізіндегі үлгілеу:
   

1. 
   ақпараттық
   
2. 
   геометриялық
   
3. 
   физикалық
   
4. 
   вербалды
   

4. 
   Түпнұсқаның кеңістіктегі пішіні мен пропорциясын көрсету негізіндегі үлгілеу:
   

1. 
   геометриялық
   
2. 
   ақпараттық
   
3. 
   физикалық
   
4. 
   вербалды
   

5. 
   Түпнұсқада жүретін физика – химиялық, технологиялық, биологиялық құбылыстарды зерттеу негізіндегі үлгілеу:
   

1. 
   физикалық
   
2. 
   ақпараттық
   
3. 
   геометриялық
   
4. 
   вербалды
   

6. 
   Үлгідегі барлық көрсеткіштер мәні бір квант (кезең, мезгіл) уақытына жататын үлгі:
   

1. 
   статикалық
   
2. 
   динамикалық
   
3. 
   стохастикалық
   
4. 
   түзгілік – ойын
   

7. 
   Үлгідегі көрсеткіштер мәні уақыт мөлшерінде өзгеретін үлгі:
   

1. 
   динамикалық
   
2. 
   статикалық
   
3. 
   стохастикалық
   
4. 
   түзгілік – ойын
   

8. 
   Шешім алудың программалық ережелерін білдіретін үлгі:
   

1. 
   компьютерлік
   
2. 
   математикалық
   
3. 
   физикалық
   
4. 
   аналогты
   

9. 
   Сызықты теңдеулер жүйесін шешудегі итерациалық әдістерге жататын нұсқа?
   

1. 
   ықтималдық әдістері
   
2. 
   негізгі элементтер әдісі
   
3. 
   Гаусс әдісі
   
4. 
   квадратты түбірлер әдісі
   

10. 
    Үлгілеу қандай категориямен тығыз байланысты емес?
    

1. 
   аномалия
   
2. 
   аналогия
   
3. 
   абстракция
   
4. 
   гипотеза
   

11. 
    Жылуландыру кезең қашан басталады?
    

1. 
   сыртқы ауаның орта ыстықтығы үш тәулік бойы 8 ⁰С-ден төмен болса
   
2. 
   қазан айының басында
   
3. 
   қазан айының ортасында
   
4. 
   қазан айының соңында
   

12. 
    Симплекс әдісін кім ойлап тапты?
    

1. 
   Дж. Данциг
   
2. 
   Розенборг
   
3. 
   Симпсон
   
4. 
   Гаусс
   

13. 
    Сызықты емес екі көрсеткішті бір айнымалыдан тұратын тәуелділіктің R₁ аппроксимация критериі min болса, қандай эмпирикалық функция таңдаған дұрыс?
    

---

1. 
   сызықты функция
   
2. 
   көрсеткіш функция
   
3. 
   логарифмдік функция
   
4. 
   дәрежелі функция
   

14. 
    Сызықты емес екі көрсеткішті бір айнымалыдан тұратын тәуелділіктің R₂ аппроксимация критериі min болса, қандай эмпирикалық функция таңдаған дұрыс?
    

1. 
   көрсеткіш функция
   
2. 
   гиперболалық функция
   
3. 
   логарифмдік функция
   
4. 
   дәрежелі функция
   

15. 
    Сызықты емес екі көрсеткішті бір айнымалыдан тұратын тәуелділіктің R₄ аппроксимация критериі min болса, қандай эмпирикалық функция таңдаған дұрыс?
    

1. 
   логарифмдік функция
   
2. 
   гиперболалық функция
   
3. 
   көрсеткіш функция
   
4. 
   дәрежелі функция
   

16. 
    Сызықты емес екі көрсеткішті бір айнымалыдан тұратын тәуелділіктің R₅ аппроксимация критериі min болса, қандай эмпирикалық функция таңдаған дұрыс?
    

1. 
   дәрежелі функция
   
2. 
   гиперболалық функция
   
3. 
   логарифмдік функция
   
4. 
   көрсеткіш функция
   

17. 
    Сызықты емес екі көрсеткішті бір айнымалыдан тұратын тәуелділіктің R₆ аппроксимация критериі min болса, қандай эмпирикалық функция таңдаған дұрыс?
    

1. 
   гиперболалық функция
   
2. 
   дәрежелі функция
   
3. 
   логарифмдік функция
   
4. 
   көрсеткіш функция
   

18. 
    Сызықты емес екі көрсеткішті бір айнымалыдан тұратын тәуелділіктің R₃ аппроксимация критериі min болса, қандай эмпирикалық функция таңдаған дұрыс?
    

1. 
   бөлшекті – рационал функция
   
2. 
   дәрежелі функция
   
3. 
   логарифмдік функция
   
4. 
   көрсеткіш функция
   

19. 
    Жәй дифференциалдық теңдеулерді сандық шешудегі Коши есептері қандай типке жатады?
    

1. 
   1 – ші типке
   
2. 
   2 – ші типке
   
3. 
   3 – ші типке
   
4. 
   4 – ші типке
   

20. 
    Кәдімгі дифференциалдық теңдеулерді сандық шешу неше классқа бөлінеді?
    

1. 
   2
   
2. 
   3
   
3. 
   1
   
4. 
   4
   

21. 
    Кәдімгі дифференциалдық теңдеулерді сандық шешудегі көп қадамды әдіске жатады:
    

1. 
   болжау әдісі
   
2. 
   Эйлер әдісі
   
3. 
   Рунге – Кутта әдісі
   
4. 
   Адаммс әдісі
   

22. 
    Кәдімгі дифференциалдық теңдеулерді сандық шешудегі көп қадамды әдіске жатады:
    

1. 
   түзету (коррекция) әдісі
   
2. 
   Эйлер әдісі
   
3. 
   Рунге – Кутта әдісі
   
4. 
   Адаммс әдісі
   

23. 
    Кәдімгі дифференциалдық теңдеулерді сандық шешудегі бір қадамды әдіске жатады:
    

---

1. 
   Эйлер әдісі
   
2. 
   Милн әдісі
   
3. 
   болжау әдісі
   
4. 
   түзету (коррекция) әдісі
   

24. 
    Кәдімгі дифференциалдық теңдеулерді сандық шешудегі бір қадамды әдіске жатады:
    

1. 
   Рунге – Кутта әдісі
   
2. 
   болжау әдісі
   
3. 
   түзету (коррекция) әдісі
   
4. 
   Милн әдісі
   

25. 
    Кәдімгі дифференциалдық теңдеулерді сандық шешудегі бір қадамды әдіске жатады:
    

1. 
   Адаммс әдісі
   
2. 
   болжау әдісі
   
3. 
   түзету (коррекция) әдісі
   
4. 
   Милн әдісі
   

26. 
    Бір сатылы буландырғыш (испаритель) өнімділігі бу қазан өнімділігінің неше пайызын құрайды?
    

1. 
   2 – 4 %
   
2. 
   8 – 12 %
   
3. 
   15 – 20 %
   
4. 
   20 – 25 %
   

27. 
    Бір сатылы буландырғыш (испаритель) өнімділігі желі су өнімділігінің неше пайызын құрайды
    

1. 
   8 – 12 %
   
2. 
   2 – 4 %
   
3. 
   15 – 20 %
   
4. 
   20 – 25 %
   

28. 
    Сызықты теңдеулер жүйесін шешудегі дәл әдістерге жататын нұсқа?
    

1. 
   квадратты түбірлер әдісі
   
2. 
   Зейдел әдісі
   
3. 
   релаксация әдісі
   
4. 
   ықтималдық әдістері
   

29. 
    Сызықты теңдеулер жүйесін шешудегі дәл әдістерге жататын нұсқа?
    

1. 
   Гаусс әдісі
   
2. 
   Зейдел әдісі
   
3. 
   релаксация әдісі
   
4. 
   ықтималдық әдістері
   

30. 
    Сызықты теңдеулер жүйесін шешудегі дәл әдістерге жататын нұсқа?
    

1. 
   негізгі элементтер әдісі
   
2. 
   Зейдел әдісі
   
3. 
   релаксация әдісі
   
4. 
   ықтималдық әдістері
   

31. 
    Сызықты теңдеулер жүйесін шешудегі итерациалық әдістерге жататын нұсқа?
    

1. 
   Зейдел әдісі
   
2. 
   негізгі элементтер әдісі
   
3. 
   Гаусс әдісі
   
4. 
   квадратты түбірлер әдісі
   

32. 
    Сызықты теңдеулер жүйесін шешудегі итерациалық әдістерге жататын нұсқа?
    

1. 
   релаксация әдісі
   
2. 
   негізгі элементтер әдісі
   
3. 
   Гаусс әдісі
   
4. 
   квадратты түбірлер әдісі
   

33. 
    Сызықты теңдеулер жүйесін шешуде қандай әдісте компьютер көмегімен есептеу қолданылмайды?
    

1. 
   Крамер ережесі
   
2. 
   релаксация әдісі
   
3. 
   негізгі элементтер әдісі
   
4. 
   квадратты түбірлер әдісі
   

34. 
    Алтын кесінді әдісіндегі кесінділердің қатынасы?
    

1. 
   0,618
   
2. 
   1,5
   
3. 
   0,5
   
4. 
   (а – в)/3
   

35. 
    Кімнің тәуелділік формулалары су және су буының күй көрсеткіштерін анықтауда тек изоэнтропамен жүргізіліп, қаныққан бу сызығындағы көрсеткіштерімен салыстырылып отырады?
    

---

1. 
   Индруский М.С.
   
2. 
   Ривкин С.Л.
   
3. 
   Юза Я.
   
4. 
   Александров А.А.
   

36. 
    Кесіндіні қаққа бөлу (дихотомия) әдісінде сызықты емес теңдеулердің түбірлерін анықтау дәлдігі келесі нұсқамен бағаланады:
    

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   

37. 
    Ньютон (жанамалар) әдісінде сызықты емес теңдеулердің түбірлерін анықтау дәлдігі келесі нұсқамен бағаланады:
    

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   

38. 
    Пропорционалды бөліктер (хорда) әдісінде сызықты емес теңдеулердің түбірлерін анықтау дәлдігі келесі нұсқамен бағаланады:
    

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   

39. 
    Жәй итерация әдісінде сызықты емес теңдеулердің түбірлерін анықтау дәлдігі келесі нұсқамен бағаланады:
    

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   

40. 
    Анықталған интегралдарды сандық есептеудегі тіктөртбұрыштар әдісінің формуласы:
    

---

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   

41. 
    Анықталған интегралдарды сандық есептеудегі трапециялар әдісінің формуласы:
    

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   

42. 
    Анықталған интегралдарды сандық есептеудегі параболалар (Симпсон) әдісінің формуласы:
    

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   

43. 
    Анықталған интегралдарды сандық есептеудегі Монте – Карло әдісінің формуласы:
    

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   

44. 
    Келесі кейіптемедегі интерполяциялық формула
    

1. 
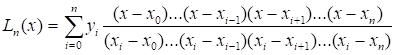
   Лагранж интерполяциялық формуласы
   
2. 
   Ньютонның екінші интерполяциялық формуласы
   
3. 
   Ньютонның бірінші интерполяциялық формуласы
   
4. 
   Стирлинг интерполяциялық формуласы
   

---

Смотрите также файлы

• ндірістік (психологиялыпедагогикалы) істжірибе Производственная.pptx

• Лабораторная работа 1 Исследование согласованных фильтров студент Проверила Цель работы.docx

• Цель образовательной и воспитательной деятельности в сфере экологии это становление начал экологической культуры у детей развитие экологического сознания, мышления и экологической культуры у взрослых, их воспитывающих.rtf

• Createdatabase.docx

• Муниципальное право.docx