Задача 1

В урне содержится 8 белых и 6 красных шаров. Случайным образом вынимают 4 шара. Какова вероятность того, что среди них имеется:

А) ровно 3 белых шара;

Б) меньше, чем 3 белы шаров;

В) хотя бы 1 белый шар.

Решение:

А) Пусть событие А – среди вынутых шаров ровно три белых (тогда 1 вынутый шар – черный). Вероятность этого события найдем, используя классическое определение вероятностей:

, где n – число элементарных исходов, благоприятствующих данному событию.

Элементарными исходами являются сочетания из 14 элементов по 4, т.е.



Число исходов, благоприятствующих данному событию:



Получим

Б) Пусть событие В – среди вынутых шаров меньше чем 3 белых шара. Это возможно, когда вынули 0 белых и 4 черных шара, или 1 белый и 3 черных, или 2 белых и 2 черных.

Поэтому

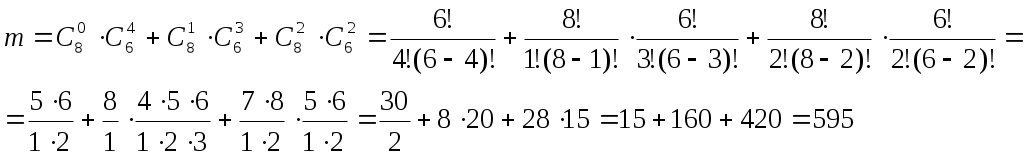
Получаем

В) Пусть событие С – среди вынутых шаров хотя бы один белый шар.

Перейдем к противоположному событию - среди вынутых шаров нет ни одного белого, т.е. все шары – черные. Следовательно,



Получаем:

Тогда Р(С)=1-0,0149=0,9851

Ответ: а) 0,3357, б) 0,5944, в) 0,9851

Задача 2

Для получения кредита предприятие обратилось к трем банкам.

Статистические исследования показали, что вероятности выделения кредита этими банками оценивается следующим образом: для первого банка р

---

₁=1/4, для второго банка р₂=1/6 и для третьего р₃=1/8.

Банки выделяют кредит независимо друг от друга, и если примут решение о его выделении, в размере: первый банк – 15 млн.руб., второй – 25 млн.руб., третий – 10 млн.руб. Рассмотрим следующие события:

А –первый банк выделил кредит;

В – второй банк выделил кредит;

С – третий банк выделил кредит.

Интересы предприятия, обратившегося за кредитом, описываются событиями:

Д- получен кредит 25 млн.руб.;

Е – получен кредит не менее 25 млн.руб.

Выразить эти события через события А,В,С и найти и вероятности.

Решение:

Рассмотрим событие Д. предприятие получит кредит 25 млн.руб. в двух случаях:

1. 
   Первый и третий банк выделили кредит, а второй не выделил – событие Д₁.
   
2. 
   Кредит выделит только второй банк, а первый и третий не выделят – событие Д₂.
   

При этом события Д₁ и Д₂ – несовместны и Д=Д₁+Д₂.

Событие Д₁ будет иметь место, если одновременно будут иметь место события А, не В и С. Значит,

Аналогично получаем .

Получим



Р(Д)=1/4*(1-1/6)*1/8+(1-1/4)*1/6*(1-1/8)=0,25*0,83*0,13+0,75*0,17*0,87

= 0,0269+0,1109=0,1378

Событие Е произойдет в трех случаях:

1. 
   Предприятие получит кредит 40 млн.руб. – Е₁
   
2. 
   Предприятие получит кредит 35 млн.руб. – Е₂
   
3. 
   Предприятие получит кредит 50 млн.руб. – Е₃
   

При этом , ,



Ответ: Р(Д)=0,1378; Р(Е)=0,059

Задача 3

На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: 40 –с первого завода, 35 – со второго завода, 25 – с третьего завода. Вероятность качественного изготовления изделий на первом заводе 0,9; на втором – 0,7; на третьем – 0,9.

---

Какова вероятность того, что взятое случайным образом изделие будет качественным? Какова вероятность того, что качественное изделие будет с первого завода?

Решение:

Комплектующие изделия поступили с трех заводов 1- 40, 2-35, 3- 25. Всего 40+35+25=100 изделий.

Испытание: случайным образом берется одно изделие.

Событие А связано с гипотезами:

В₁- взятое изделие изготовлено на первом заводе;

В₂ – взятое изделие изготовлено на втором заводе;

В₃ – взятое изделие изготовлено на третьем заводе.

В₁, В₂, В₃ – образуют полную группу несовместных событий, т.к. заводов только три и взяли только одно изделие.

Можно использовать формулу полной вероятности:



Р(В₁), Р(В₂), Р(В₃) можно найти по определению



, ,

Подставим данные значения в формулу полной вероятности, получим:

Р(А)=0,4*0,9+0,35*0,7+0,25*0,9=0,36+0,245+0,225=0,83

Вероятность того, что качественное изделие будет с первого завода, найдем по формуле Байеса:

Ответ: Р(А)=0,83, Р_А(В₁)=0,4337

Задача 4

В городе 3 оптовых базы. Вероятность того, что требуемого сорта товар имеется на этих базах одинакова и равна 0,8. Составьте закон распределения числа баз, на которых искомый товар имеется. Найти математическое ожидание, дисперсию дискретной случайной величины.

Решение:

Дано: 3 оптовых базы.

Испытание: ищем товар требуемого сорта на каждой из 3-х баз.

Событие А – товар требуемого сорта имеется на любой из трех баз. Р(А)=0,8.

---

Случайная величина Х – число баз, на которых требуемый товар имеется.

Чтобы составить закон распределения дискретной случайной величины Х необходимо указать соответствие между возможными значениями случайной величины и вероятностями их появления. Записать этот закон можно в виде ряда распределения. Случайная величина Х принимает значения 0,1,2,3. Вероятность события А на всех 3-х базах одинакова, поэтому можно использовать формулу Бернулли:

,

Р=0,8; q=1-0,8=0,2

хi	0	1	2	3
pi	0,008	0,096	0,384	0,512

Контроль вычислений: 0,008+0,096+0,384+0,512=1.

Математическое ожидание дискретной случайной величины найдем по определению:





Для нахождения дисперсии воспользуемся свойством:

D(X)=M(X²)-(M(X))².

D(X) =(0*0,008+1*0,096+4*0,384+9*0,512)-(2,4)²=0,096+1,536+4,608-5,76=0,48

Ответ: М(Х)=2,4; D(Х)=0,48.
Задача 5

Дискретная случайная величина задана таблицей:

хi	-5	-2	0	2	5
pi	1/46	1/8	1/2	1/3	p5

Найти р₅, математическое ожидание, дисперсию, среднее квадратическое отклонение. Построить многоугольник распределения. Найти и изобразить графическую функцию распределения.

Решение:

Для любой дискретной случайной величины

Получаем 1/46+1/8+1/2+1/3+р

---

₅=1

0,02+0,13+0,5+0,33+р₅=1

Р₅=1-0,02-0,13-0,5-0,33=0,02

Т.е ряд распределения имеет вид:

хi	-5	-2	0	2	5
pi	0,02	0,13	0,5	0,33	0,02

Математическое ожидание найдем по формуле:

Получаем М(Х)=(-5)*0,02+(-2)*0,13+0*05+2*0,33+5*0,02=

=-0,1-0,26+0+0,66+0,1=0,4

Дисперсию найдем по формуле D(X)=M(X²)-(M(X))².

М(Х²)=25*0,02+4*0,13+0*0,5+4*0,33+25*0,02=0,5+0,52+0+1,32+0,5=

=2,84

Тогда D(X)=2,84-(0,4)²=2,84-0,16=2,68

Среднее квадратическое отклонение найдем по формуле:

Получаем

Построим многоугольник распределения:

Если -5 , то F(x)=0.02+0.13+0.5+0.33+0.02

Функция распределения задается формулой F(x) =P(X
Будем задавать различные значения х и находить соответствующие значение функции:

Если х , то F(x)=0

Если то F(x)=0,02

Если то F(x)=0,02+0,13=0,15

Если то F(x)=0,02+0,13+0,5=0,65

Если то F(x)=0,02+0,13+0,5+0,33=0,98

Если то F(x)=0,02+0,13+0,5+0,33+0,02=1

Получаем:



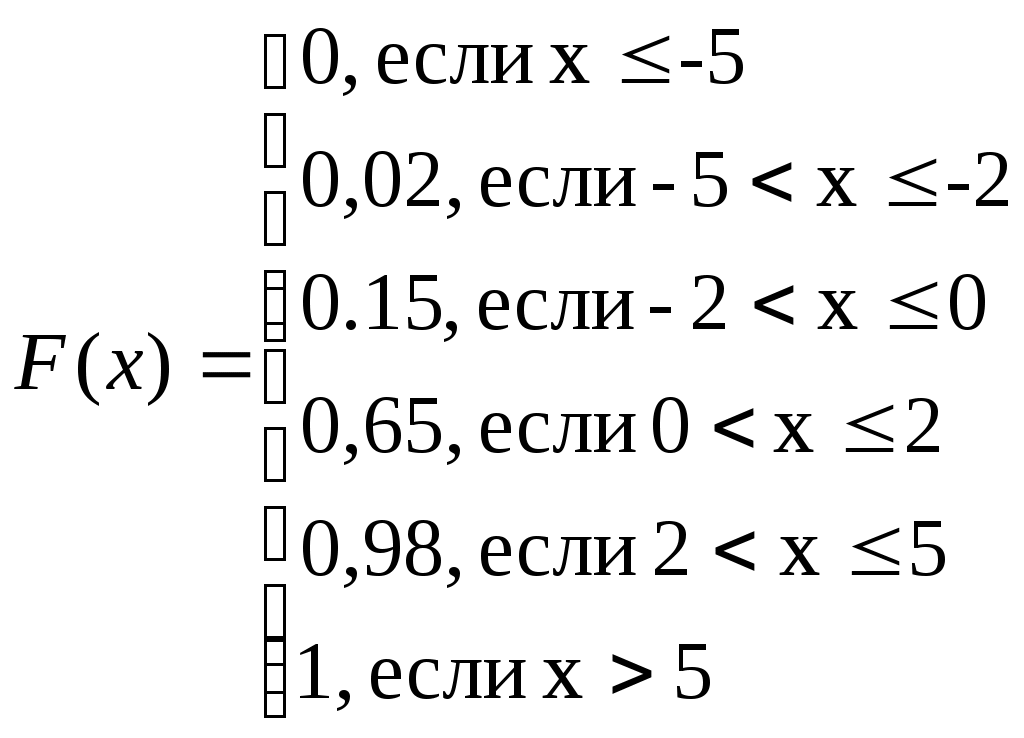
Построим график функции распределения:

:






1

---

Смотрите также файлы

• Программа среднего профессионального образования 38. 02. 03 Операционная деятельность в логистике Дисциплина Менеджмент Практическое задание 2.doc

• Дата 16. 05 Соч 4 четверть 9 В класс Ф. И. учащегося задания.docx

• Контрольная работа Информатика и информационные технологии в профессиональной деятельности.docx

• Зиккурат храм в виде высокой ступенчатой башни в Месопотамии. Иштар.docx

• алыптастырушы баалауа арналан тапсырмалар жинаы 10сынып (Жаратылыстануматематика баыты).doc