Файл: Задача 1 в урне содержится 8 белых и 6 красных шаров. Случайным образом вынимают 4 шара. Какова вероятность того, что среди них имеется а ровно 3 белых шара б меньше, чем 3 белы шаров в хотя бы 1 белый шар. Решение.doc
Добавлен: 02.12.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.










 0
0 Задача 6
Вероятность возврата в срок потребительского кредита каждым из 220 заемщиков в среднем равна 0,95. Найти вероятность того, что к назначенному сроку кредит вернут:
А) не менее 180 человек и не более 200 человек;
Б) не менее 200 человек;
В) не более 199 человек.
Решение:
А) Согласно интегральной теореме Лапласа, если вероятность появления события А в каждом из n независимых испытаний постоянна и равна р, то вероятность того, что во всех этих испытаниях события А появится не меньше к1 раз и не более к2 раз, приближенно определяется формулой:
Рn(k1, k2) =Ф(Х2)-Ф(Х1)
Где Х1=
По условию задачи n=220, р=0,95, q=1-0,95=0,05
К1=180, к2=200
Вычислим х1=
Вычислим х2
По таблице значений функции Лапласа, учитывая нечетность этой функции, находим:
Р100(180;200)=Ф(-2,79)-Ф(-8,97)=Ф(8,97)-Ф(2,79)=0,4999-0,4973=0,0026
Б) Требование, что событие А появится не менее 200 раз, означает, что число появлений события может быть равно 200, либо 201 либо 202, …, либо 220.
Значит, в данном случае следует принять, что к1=200, к2=220
Тогда х1=-2,79, х2=3,4
Р100(200;220)=Ф(3,4)-Ф(-2,79)=0,4996-0,4973=0,0023
В) Событие (А появится не более 199) и (А появится не менее 200 раз) противоположны, поэтому
Р100(0;199)=1-Р100(180;200)=1-0,0026=0,9974
Ответ: а) 0,0026 б) 0,0023 в)0,9974
Задача 7
Непрерывная случайная величина задана функцией плотности распределения р(х).
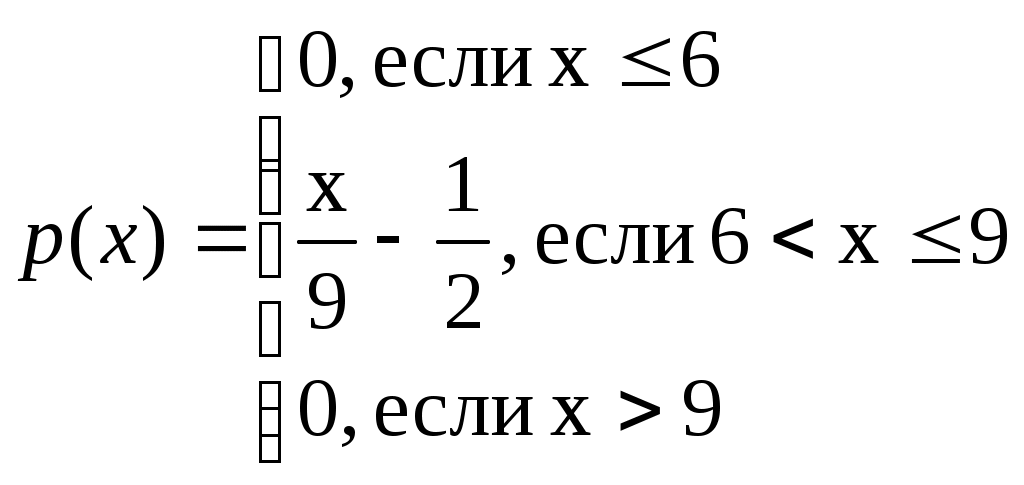
А) Найти функцию распределения F(x), построить графики функции р(х) и F(x).
Б) Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение.
В) Найти вероятность того, что случайная величина примет значение на отрезке [3;4].
Решение:
А) Функция р(х) и F(x) связаны соотношением
Если
Если
Если
Б) Математическое ожидание, дисперсию и среднее квадратическое отклонение найдем по формулам:
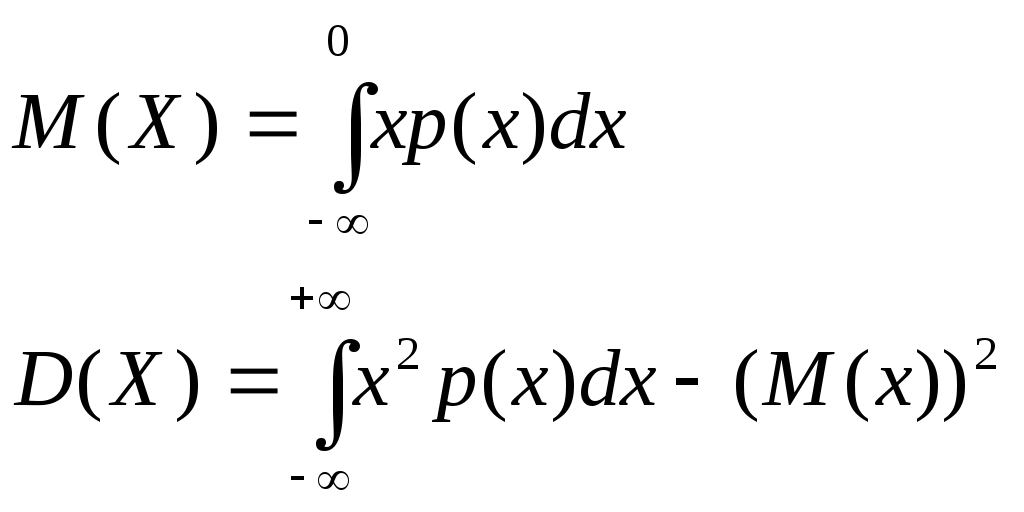
В) Вероятность того, что случайная величина примет значение на отрезке [3;4] найдем по формуле:
Ответ: б) 1; 2,8; 1,67; в) 0