Файл: Методические указания к лабораторным работам для студентов всех направлений.docx

Лабораторная работа № 5. Исследование скорости химических реакций и химического равновесия

Цель работы: изучить зависимость скорости реакции от концентрации реагентов и температуры, а также ознакомиться с влиянием концентрации реагентов на химическое равновесие.

Сущность работы: Зависимость скорость реакции от концентрации реагирующих веществ определяется кинетическим уравнением. Эту зависимость устанавливают при постоянной температуре, изменяя концентрацию одного из реагирующих веществ. Зависимость скорости реакции от температуры описывается эмпирическим правилом Вант-Гоффа (работает при температуре < 100°С) и уравнением Аррениуса. Определив параметры уравнения Аррениуса, можно рассчитать скорость реакции при любой заданной температуре.

Общие сведения

Средняя скорость реакции равна изменению молярной концентрации реагента в единицу времени при постоянстве объема системы. Единица измерения в СИ: моль/м³с. Истинная скорость реакции равна модулю производной концентрации по времени:

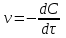. (9)

Скорость реакции пропорциональна числу столкновений между молекулами реагентов, которое определяется произведением их концентраций. Если в акте реакции участвуют несколько молекул одного из реагентов, то его концентрацию надо перемножить соответствующее число раз, то есть возвести в степень. Для одностадийной реакции типа:

А + В = (10)

скорость будет определяться так называемым кинетическим уравнением:

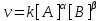, (11)

где А и В– молярные концентрации реагентов, k– коэффициент пропорциональности, называемый константой скорости реакции, и  – частные порядки реакции по данным реагентам. Константа скорости не зависит от времени протекания реакции и концентрации реагентов, но зависит от природы участников реакции, температуры и присутствия катализаторов и имеет физический смысл скорости реакции при единичных концентрациях реагирующих веществ. Порядок по реагентам A и B отражает влияние концентрации данных реагентов на скорость реакции.

---

Если реакция протекает в несколько стадий, то значения  и  могут быть не равны стехиометрическим коэффициентам в уравнении реакции. Порядок реакции в данном случае может быть найден экспериментально. Пусть требуется, например, найти порядок реакции по реагенту А. Поскольку

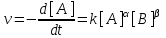, (12)

при очень малых изменениях концентрации реагентов в ходе реакции

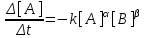. (13)

Обозначая промежуток времени Δt как τ, после логарифмирования данного выражения получим

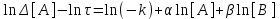, (14)

откуда

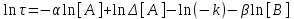. (15)

При постоянных величинах начальной концентрации второго реагента [B] и изменения концентрации реагента A в начальном периоде реакции, т. е. величины Δ[A], уравнение приобретает вид:

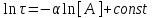(16)

Из полученного уравнения следует, что зависимость логарифма времени протекания реакции от логарифма начальной концентрации реагента A выражается прямой линией, при этом тангенс угла наклона (угловой коэффициент) равен -α. Таким образом, измерив время протекания реакции τ при различных начальных концентрациях реагента A и построив зависимость lnτ = ƒ(ln[A]), можно определить порядок реакции по данному реагенту.

Скорость реакции резко зависит от температуры. Известно эмпирическое правило Вант-Гоффа: «При увеличении температуры на 10 K скорость химических реакций возрастает в 2–4 раза»:

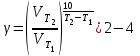(17)

где  – температурный коэффициент скорости реакции.

Причина столь значительной температурной зависимости скорости реакций в том, что для перестройки химических связей в молекулах в ходе элементарного акта реакции требуются большие затраты энергии. Расчеты показывают, что лишь одно из 10¹⁰–10²⁰ столкновений молекул реагентов заканчивается химическим превращением. В остальных случаях кинетической энергии частиц оказывается недостаточно для перестройки связей. Минимальное количество кинетической энергии молекул, необходимое для протекания элементарного акта реакции при их столкновении, называют энергией активации. Домножив ее на число Авогадро, получим молярную энергию активации

---

Е_а, которую измеряют в Дж/моль. Из закона Максвелла и Больцмана следует, что число частиц с высокими энергиями теплового движения, а значит и число активных столкновений, увеличивается экспоненциально с ростом температуры, чем и обусловлены высокие температурные коэффициенты скорости химических реакций.

В 1889 г. знаменитый шведский химик Аррениус вывел уравнение, связывающее константу скорости с температурой и энергией активации,согласно которому, константа скорости находится в экспоненциальной зависимости от температуры:

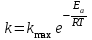, (18)

где R– универсальная газовая постоянная, равная 8,314 Дж/мольK; k_max – предэкспоненциальный фактор, имеющий смысл максимально возможного значения константы скорости при нулевой энергии активации или бесконечно высокой температуре, когда все столкновения молекул реагентов становятся активными. Уравнение Аррениуса используют чаще в логарифмической форме:

lnk = lnk_max–E_a/RT, (19)

согласно которой, графическая зависимость lnk = f(T^–1) является прямолинейной. Ее строят по опытным данным. Отрезок, отсекаемый на оси ординат при экстраполяции прямой, равен lnk_max. Угловой коэффициент равен –E_a/R. Определив параметры уравнения Аррениуса, можно рассчитать скорость реакции при любой заданной температуре.

Большинство химических реакций являются обратимыми, то есть могут протекать как в прямом, так и в обратном направлениях. Рассмотрим обратимую реакцию:

aA + bB=cC + dD

Скорости прямой и обратной реакций связаны с концентрациями реагентов следующими уравнениями:

v_пр = k_прA^aB^b; (20)

v_обр = k_обрC^cD^d. (21)

С течением времени скорость прямой реакции будет уменьшаться вследствие расхода реагентов А и В и понижения их концентраций. Напротив, скорость обратной реакции по мере накопления продуктов С и D будет возрастать. Поэтому через некоторый промежуток времени скорости прямой и обратной реакций сравняются друг с другом. Установится состояние системы, в котором отсутствуют потоки вещества и энергии, называемое химическим равновесием. Все обратимые процессы протекают не полностью, а лишь до состояния равновесия

---

, в котором из условия v_пр = v_обр следует математическое выражение закона действующих масс, который позволяет рассчитывать состав равновесной реакционной смеси:

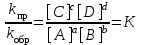, (22)

где K– константа химического равновесия, которая зависит от температуры и природы реагентов, но не зависит от концентрации последних.

Переход от одного равновесного состояния к другому в результате изменения внешних условий (температуры, давления, добавки одного из реагентов) называют смещением равновесия. Если изменение условий вызвало рост концентрации продуктов реакции, то говорят: равновесие сместилось в сторону прямой реакции. Напротив, уменьшение выхода продуктов означает смещение равновесия в сторону обратной реакции.

На практике важно добиться максимально возможного смещения равновесия в сторону прямой реакции (или обратной, если требуется подавить образование вредных веществ). Условия для этого выбирают на основе принципа, сформулированного известным французским металлургом Ле-Шателье: «равновесие смещается в сторону реакции, ослабляющей оказываемое на систему внешнее воздействие». Например, при повышении температуры равновесие смещается в сторону эндотермической реакции, протекающей с поглощением тепла. При добавлении в систему одного из реагентов, равновесие смещается в сторону реакции, в которой этот реагент расходуется.

Выполнение работы

Опыт 1. Влияние концентрации тиосульфата натрия на скорость его разложения в кислой среде

В четыре сухие пробирки внести тиосульфат натрия и воду согласно таблице.

Таблица 2

Приготовление растворов

Номер пробирки	Число капель
	Na2S2O3	H2O	H2SO4	Всего
1	4	8	1	13
2	8	4	1	13
3	12	0	1	13
4 (контрольная)	6	7	0	13

---

В первую пробирку добавить одну каплю серной кислоты и включить секундомер. Определить время от момента добавления кислоты (начала реакции) до появления явной мути за счет образующейся серы – по сравнению с пробиркой № 4. То же самое проделать с двумя другими пробирками.

Опыт 2. Влияние температуры на скорость реакции разложения тиосульфата натрия в кислой среде

Налить в одну пробирку 10 капель раствора тиосульфата натрия, в другую – 10 капель раствора серной кислоты. Обе пробирки с растворами поместить в термостат, отметить температуру по термометру и термостатировать их в течение 1–2 минут. Быстро вылить кислоту в пробирку с раствором тиосульфата, оставив последнюю в термостате. Одновременно включить секундомер и заметить время от сливания растворов до появления в пробирке явной белой мути серы.

Повторить опыт еще дважды, повышая температуру воды в термостате примерно на 10 K.

Опыт 3. Влияние катализатора на скорость реакции

В две пробирки внести по 10 капель 0,5 н. раствора роданида калия и по 1 капле 0,5 н. раствора хлорида железа (III). Что наблюдается? В одну из пробирок добавить 1 каплю 1 н. раствора сульфата меди. В обе пробирки внести по 10 капель тиосульфата натрия. Наблюдать различную скорость обесцвечивания растворов, которое происходит вследствие восстановления железа (III) до железа (II) тиосульфатом натрия.

Опыт 4. Влияние концентраций реагентов на равновесие обратимой реакции между хлоридом железа (III) и тиоцианатом аммония

В четыре пробирки налить равное число капель разбавленных растворов хлорида железа (III) и тиоцианата аммония. Первую пробирку оставить как эталон для сравнения; во вторую пробирку прилить несколько капель концентрированного раствора FeCl₃; в третью пробирку добавить несколько капель концентрированного раствора NH₄CNS; в четвертую пробирку на кончике шпателя прибавить кристаллического хлорида аммония и взболтать.

Сопоставить цвета растворов во всех пробирках и сделать выводы о направлении смещения равновесия, учитывая, что в реакции:

FeCl₃ + 3NH₄CNS = Fe(CNS)

---