Файл: Методика изучения последовательностей и их пределов. Длина окружности и площадь круга.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 02.12.2023

Просмотров: 278

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

  1. Методика изучения последовательностей и их пределов. Длина окружности и площадь круга.

  2. Методика изучения арифметической и геометрической прогрессий.
Определение: числовой последовательностью наз. числовая функция натурального аргумента xn=f(n)Задать числовую последовательность значит задать правило, по которому каждому натуральному числу n соответствует одно и только одно число.Способы задания последовательности:1)аналитический- с помощью формулы n-го члена последовательности, по которой могут быть вычислены все остальные2)табличный3)рекуррентный4)словесныйВиды:1)последовательность наз.убывающей(строго) если каждый её следующий член меньше предыдущего2) последовательность наз. возрастающей(строго) если каждый её следующий член больше предыдущего3) последовательность наз. неубывающей если каждый её следующий член не меньше предыдущего4) последовательность наз.не возрастающей если каждый её следующий член не больше предыдущегоПрогрессии1)Арифметической прогрессией наз. числовую последовательность, каждый член которой, начинается со второго, равен предыдущему члену, сложенному с одним и тем же числом, это число наз. разностью арифметической прогрессии и обозначают буквой d.an=a1+d(n-1)2) Геометрической прогрессией наз. числовую последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же число, не равное нулю.bn+1=bnqАрифметическая и геометрическая прогрессии являются примерами последовательностей, изучаемых в школьном курсе,которые в свою очередь являются примерами ф-й с натуральным аргументом. Тем самым устанавливается связь этих прогрессий с ф-ми. Однако функциональный подход к прогрессиям сам по себе большого интереса не представляет, в школьном курсе дело сводиться к вычислительным задачам, решаемым на основе ф-л общего члена и суммы n членов этих прогрессий. Отдельный интерес представляет вопрос о сумме членов бесконечно убывающей геомет. прогрессии. хотя вопрос о прогрессиях дошкольного курса является традиционным тем не менее, большого применения он в нем не находит. Одно из типичных применений- вывод правил перевода бесконечной десятичной периодич.дроби в обыкновенную, которая для теперешнего базового уровня обучения, не является доступной.

  1. Предел функции и непрерывность.
Понятие предела – одно из важнейших понятий курса математического анализа. Однако исторически теория пределов сформировалась позднее в 19 в, чем дифференциальное и интегральное исчисление (17в).Определение предела чрезвычайно сложно, поэтому в общеобразовательной школе можно обойтись без строгой его формулировки. Но не зависимо от того, на каком уровне вводиться понятие надо соблюдать следующее:- Проводить мотивацию изучения, например, с помощью примеров из физики, используя генетический подход, внутренние потребности самой математики.- Везде где это возможно вводить определение, сформулировать свойства и т.д., исходя из геометрически наглядных соображений, использовать графики функции.Тема начинается с изучения понятия предела числовой последовательности.Мотивацией могут служить внутренние потребности математики, так как ранее учащиеся уже сталкивались с термином предел, предельный переход. Поэтому настало время дать четкое определение этому понятию.Актуализация должна включать следующие упражнения:1). повторение формул нахождения расстояния между 2 точкам на числовой прямой х1(х1) х2(х2)d(x1, x2) = |x1-x2|2) показать на числовой оси множество точек удовлетворяющие равенствуа) |x-a|=bб) |x-a|где a и b – фиксированные числа.3). Решить неравенство |x – a| < b (b > 0)-b < x-a < b -b+a < x < b+a - запись окружности вокруг точки а радиуса bДалее на основе решения последних упражнений вводится понятие окружности числа (точки). Окрестность т.а радиуса b.Затем рассматривается последовательность:аn=(2n-1)/n- Выпишем несколько первых членов последовательностиa1=…=1а2=…=3/2a3=…=5/3 ….- Изобразите полученные числа на числовой прямой (рисуем)- Можно ли указать сотый (тысячный) член этой последовательности, a1000 ? (да)a100 =1,99a1000=1,999- можно ли их изобразить на числовой прямой? (Можно, изображаем)- существует ли число, к которому приближаются все члены последовательности с возрастанием номера? (да к 2)- итак, при возрастании номера n члены последовательности приближаются к числу 2. Значит, расстояние между числами и числом 2 уменьшается. Найдем, например, d(a
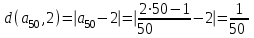
50,2)аналогично d(a100,2)- Можно ли решить обратную задачу, т.е. найти такой член последовательности (его номер n0), что d(an0, 2) < 1/200|a0 – 2| < 1/200 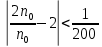, ,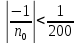 , 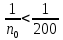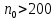.т.о. n0 =201, 202 ,…- Можно ли для данного расстояния найти номер? В этом случае говорят, что члены последовательности с номерами больше, чем 200 будут находиться, в окружности числа 2 с радиусом 1/200.Это записывается 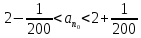,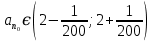..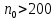- Т.о. в этой окружности содержится бесконечное, число членов последовательности, а вне этой окружности – конечное множество членов, т.е. какое бы малое положительное число ε мы не задали, обязательно найдется такое число N(номер), что все члены последовательности с номерами больше, чем N будут находиться в заданной окружности числа 2 с радиусом ε. В этом случае говорят, что число 2 является пределом последовательности an. 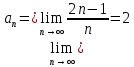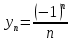Далее рассматривается еще одна аналогичная последовательность, например: Выполняется аналогичная работа с этой последовательностью. Фактически еще раз проговаривается определение, которое далее формулируется в двух видах.

Число А называется пределом числовой последовательности xn при n→∞, если

какую бы окружность числа не взяли, то все члены последовательности, начиная с некоторого номера, попадают в эту окружность.
для любого сколь угодно малого ε>0 найдет такой номер N, что для всех n>N выполняется неравенство | xn - A|<ε

на языке окрестностей
на языке ε-N:
Выполняется упражнение на осознание и осмысление определения при рассмотрении конкретных числовых последовательностей. К уроку, на котором будет изучаться определение предела функций в точке, учащимся надо предложить выполнить следующее задание:1) доказать, что lim(n-1)/3n=1/3 и т.д.2) построить графики функцийа)y=2x+1b)y=(2x2-x-1)/(x+1), получим y=2x+1, x≠1в) у=система: (2x2-x-1)/(x+1) при х≠12, при х=1г) у=система: 2x+1, при x<12-x, при x 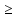1На уроке вспоминается определение предела числовой последовательности и что означает неравенство |Хn - A| < ε - имеется ε-окружность точки А- А-ε < Хn < A+ε - расстояние между точками Xn и А меньше εМотивация.Рассматривается пример из физики:- Если масса груза m увеличивается незначительно, то длина нити lмало изменяется. Но если масса груза близка к некоторой критической предельной массе m* (пределу прочности нити), то происходит обрыв нити.Изобразим это графически:Т 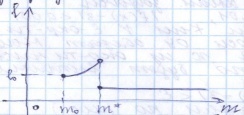акие процессы в физике встречаются довольно часто, поэтому перед нами стоит математическая задача: Найти математический аппарат (модель) с помощью которого можно описать эти процессы.Разрыв графика связан с пределом функции в точке. 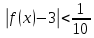Рассмотрим график новой функции y = 2x+1 из д/з (строим)- С какой бы стороны (лево, право) мы по оси Ох не двигались при х →1, f(x)→3.Рассмотрим существуют ли такие значения х при которых |2x + 1 – 3| < 0,1; |2x – 2| < 0,1; 2 – 0,1 < 2x < 2 + 0,1; 1,9 < 2x < 2,10,95 < x < 1, 05 – получилась окружность числа 1 по оси Ох.Аналогично решаются неравенства: |f(x) – 3| < 0,001, |f(x) – 3| < 0,0001Т.е. при рассмотрение любой ε-окрестности числа 3 по оси Оу обязательно найдутся такие числа х из окрестности числа 1 по оси Ох, что будет выполнятся неравенство |f(x) – 3| < ε. 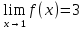(Иллюстрируют на рисунке).В этом случае говорят, что существует предел функции в точке Аналогично показывается по графику другой функции.y=(2x2-x-1)/(x+1), получим y=2x+1, x≠1 (рисуем, (1, 3) – выколота).Рассуждая аналогично, получаем
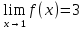
у=система: (2x2-x-1)/(x+1) при х≠12, при х=1(рисуем, (2, 3) – выколота). Аналогично рассуждая полчим тот же вывод.у=система: 2x+1, при x<12-x, при x 1(рисуем, (1, 3) – выколота).- Пусть х →1. Можно ли указать значение к которому стремится у? (Нет, нельзя, т.к. зависит от того, с какой стороны двигаемся по оси Ох).В этом случае говорят, что не существует предела функции в точке. Анализируя примеры формулируем определение.На языке ε-окресностей :Число b называется пределом функции у = f(x) при x→a , если любая ε-окрестности точки b найдется такая δ-окрестности точки а, что для всех х из этой окрестности, кроме быть может самой точки а, значения функции f(x) лежит в ε-окрестности точки b .На языке ε-δ:Число b называется пределом функции у = f(x) при x→a, если для любой ε>0, существует δ>0 ,что при всех х ≠ а, удовлетворяющих неравенству |x-a| < δ выполняется неравенство |f(x) - b|<ε.- Из приведённых определений следует, что для существования предела функции в точке, надо чтобы функция была определена во всех точках некоторой окружности данной точки, кроме быть может самой заданной точки.Для осознания и осмысления решаются задачи:1) вставить пропущенные слова в определении2) указать предел функции в точке3) доказать, что функция не имеет предела в заданной точке (методом от противного).Далее по имеющимся графикам функций отвечаем на вопросы:1) определена ли функция в точке х=1. Если да, то найти f(1)2) существует ли предел при х→1, f(х). Если да, то указать его.3)выполняется ли равенство lim f(x)=f(1) при x→1Следовательно, только для функции y=2x+1 все ответы на данные вопросы положительные. И только ее график можно построить, не отрывая мел от доски. такая функции называется непрерывной, остальные разрывные.Опр. Функция y=f(x) называется непрерывной в некоторой точке а, если lim f(x) = f(a) при x→aФункция называется непрерывной на промежутке, если непрерывна в каждой точке промежутка.В учебнике Ш.А.Алимова и др. данное подробно не рассматривается, поэтому учитель сам решает в зависимости от уровня класса, на сколько углубляется в изучение данной темы.

  1. Методика введения понятия производной. Геометрический и физический смысл производной.

Смотрите также файлы