) и любых положительных x и y, выполнены равенства:

1. log_a1=0

2. log_aa=1

3. log_axy= log_ax+ log_ay

4. log_ax/y= log_ax- log_ay

5. log_ax^p= plog_ax

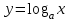Изучение логарифмической функции начинается с выделения определения: функцию, заданную формулой называют логарифмической функцией с основанием . Основные свойства выводится из свойств показательной функции:

1. ,

2. ,

3. Логарифмическая функция на всей области определения возрастает (при a>1) или убывает (при 0
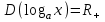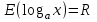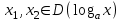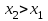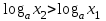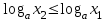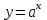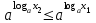
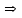
Покажем, что при a>1 возрастает. Пусть и , надо доказать, что: . Допустим противное, т.е. что . Т.к. показательная функция при a>1 возрастает, то из неравенства 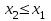следует: , что противоречит выбору 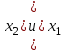. Следовательно: и функция при a>1 – возрастает.

Т.к. при a>1 функция возрастает, то логарифмическая функция положительна при x>1 и отрицательна для 0
12.Геометрические преобразования графиков функций.




13.Методика изучения элементов комбинаторики в школе.

Элементы комбинаторики — основа для вычисления вероятностей событий в широком классе вероятностных схем. Элементы методики изучения комбинаторики в школьном курсе математики были достаточно подробно разработаны, так как этот раздел изучался в школьном курсе математики в советской школе вплоть до 80-х гг. XX в. В настоящее время происходит возврат к разделу комбинаторики, так как он используется в теории

---

вероятностей и востребован в дискретной математике, широко применяемой в различных областях знания, например в информатике.

Тема «Элементы комбинаторики» может изучаться и вне контекста изучения теории вероятностей, так как она содержательно богата как в теоретическом, так и в прикладном аспектах.

Основное внимание при изучении комбинаторики следует уделить задачам, поскольку объем теоретического материала чрезвычайно мал: формулы комбинаций без повторений (перестановки, сочетания, размещения). Вопрос о необходимости аккуратного вывода формул на уроках решается учителем в соответствии с логикой используемого учебника и уровнем подготовки учеников. Возможен и вариант, когда формула появляется как обобщение результата конкретной задачи.

Основные проблемы возникают у учителя и школьников при решении комбинаторных задач. Они преодолеваются за счет правильно составленного набора задач по теме и обучения поиску решения (выбору соответствующей формулы). Прежде всего в набор должны быть включены несложные модельные задачи, которые позволяют решить их «вручную» — перебором всех возможных вариантов (составлением дерева вариантов). Такой способ решения позволит в дальнейшем при вычислении классической вероятности наступления события «вручную» составить пространство элементарных исходов. Подобные задачи можно найти в объяснительном тексте любого учебника.

Для обучения выбору формулы можно рассмотреть с учениками следующие задачи.

Задачи:

В турнире участвуют 5 человек. Сколькими способами могут распределиться места между ними?

Сколькими способами можно выбрать 3 ленты разных цветов из 5 лент разных цветов?

Сколько трехзначных чисел можно составить из цифр 1; 2; 3; 4, если цифры в записи чисел не повторяются?

Решив эти задачи с учениками, учитель делает вывод о выборе формул при решении комбинаторных задач: если в каждой комбинации участвуют все элементы множества, то это перестановки (задача 22.1). Если каждая комбинация состоит из некоторых элементов множества, то это — сочетания или размещения (задачи 22.2 и 22.3). Если в таких комбинациях важен порядок, то это — размещение (задача 22.3). Если нет, то сочетание (задача 22.2).

После чего можно рассмотреть более содержательные задачи на комбинации, например такую.

Задачи:

Сколько четырехзначных чисел можно составить из цифр 0; 2; 5; 7; 8; 9, если цифры в записи чисел нс повторяются?

---

В этой задаче нужно из числа размещений исключить те, первый элемент которых является нулем.

Для введения правил сложения и умножения можно использовать следующие простейшие задачи.

Задачи:

Сколько существует способов выбора одного карандаша из коробки, содержащей 5 красных, 7 синих и 3 зеленых карандаша?

Работая с этими задачами, необходимо сделать вывод, что в первом случае мы выбираем или один красный, или один синий, или один зеленый карандаш (правило сложения), а во втором случае - одну коробку конфет и одну коробку печенья (правило умножения). Этот опыт потребуется ученикам при решении задач на вычисление вероятности сложных событий.

Комбинации с повторениями возможно рассмотреть на внеклассных занятиях по математике.

Изучение комбинаторики важно и продиктовано самой жизнью. Классы задач, решаемые комбинаторными методами, очень многообразны. Для развития логики рассуждений, интуиции, мышления и многого другого, человеку для начала следует ознакомиться со способами решения основных задач.

Обучение комбинаторике нужно начинать с решения легких комбинаторных задач методом непосредственного перебора. Операция перебора, служит основой для формирования комбинаторных понятий и хорошей подготовкой к выводу комбинаторных формул и закономерностей и раскрывает идею комбинирования.

После того как ученики научаться создавать наборы из элементов заданного множества по заданному свойству, на первый план выходит задача по подсчету количества возможных наборов. Такие комбинаторные задачи решаются с помощью рассуждений, раскрывая принцип умножения. Оптимальной визуальной иллюстрацией правила умножения является дерево возможных вариантов. Важно показать его использование при решении комбинаторных задач.

14.Методика изучения элементов теории вероятностей в школе.

15.Методика изучения элементов статистики в школе.

16.Различные трактовки понятия функции. Функциональная пропедевтика в 5-6 классах

1>1>

---

Смотрите также файлы

• 2. 1 Моделирование бизнеспроцессов.docx

• Практическое задание 1 по учебному курсу Надзор и контроль в сфере безопасности.docx

• Программа внеурочной деятельности Разговоры о важном 1011 класс 35 часов Классный руководитель 11 А класса.docx

• Главный же вопрос данной статьи.docx

• Как неприятно бывает, когда над головой сгущаются тучи и появляется дождь, гроза или снег! Ненавистная погода может испортить настроение и планы на весь день.docx