1) понимание учащимися взаимосвязи между операциями дифференцирования и интегрирования функций, а также основной идеи метода дифференциального и интегрального исчислений;

2) осознание учащимися того факта, что аппарат производной и интеграла - основа метода математического анализа.

С одной стороны, он выступает как язык, описывающий многие явления, процессы мира. С другой - как инструмент, с помощью которого с учётом особенностей языка исследуются эти явления и процессы.

Основу содержания темы составляют два типа вопросов, каждый из которых группируется около двух понятий: "Первообразная", "Интеграл". Основное внимание при изучении уделяется:

1) нахождению первообразных и вычислению интегралов на базе таблиц первообразных и правил нахождения первообразных;

2) вычислению площадей криволинейной трапеции.

В качестве основных задач, решённых в процессе изучения темы, можно выделить следующие:

· введение понятий первообразной и интеграла;

· ознакомление учащихся с основными свойствами первообразных и правилами нахождения первообразных;

· раскрытие смысла операции интегрирования как операции, обратной по отношению к операции дифференцирования заданной функции:

· провести классификацию типов задач (нахождение площади криволинейной трапеции, нахождение объёма тела, задачи с физическим содержанием), показать, каким образом реализуется метод интегрального исчисления. При этом обратить внимание на выделение в процессе их решения этапов, характеризующих процесс математического моделирования.

Теоретический материал включает в себя понятия первообразной и её основное свойство понятие интеграла функции; связь между понятиями "интеграл" и "первообразная", которая устанавливается с помощью формулы Ньютона-Лейбница; формула Ньютона-Лейбница как аппарат вычисления интеграла данной функции. Перечисленные понятия вводятся на дедуктивной основе, дается иллюстрация использования определения основного понятия, его свойств с помощью конкретных примеров.

Задачи, помимо использования их как средства иллюстрации вводимого в рассмотрение теоретического материала, служат средством его закрепления, о чем свидетельствуют и их формулировки, например: "Найти такую первообразную функцию, график которой проходит через данную точку".

Методическая схема изучения первообразной функции

---

. В школьном учебнике были "испытаны" различные варианты введения понятия интеграла. В первых изданиях учебного пособия (под ред. А.Н. Колмогорова) интеграл определяется с помощью формулы Ньютона-Лейбница (как приращение первообразной), в более поздних изданиях применялось традиционное определение интеграла как предела интегральных сумм.

Методическая схема изучения первообразной: 1) рассмотреть примеры взаимно обратных операций; 2) ввести интегрирование как операцию, обратную дифференцированию, а первообразную как результат операции интегрирования; 3) выполнить упражнения типа: "Доказать, что данная функция есть первообразная другой данной функции ", "Решить задачи на отыскание первообразной для данной функции "; 4) ознакомить учащихся с основным свойством первообразной; 5) составить таблицу первообразных; 6) ознакомить учащихся с правилами нахождения первообразных; 7) решить физические задачи с применением первообразной.

Определению первообразной предшествует задача из механики: Если в начальный момент времени скорость тела равна 0, т.е., то при свободном падении тело к моменту времени пройдет путь: . Продифференцировав ее, получаем; - ускорение постоянно. Более типично для механики иное: известно ускорение точки, требуется найти закон изменения скорости и координату. Для решения таких задач служит операция интегрирования.

При введении понятия первообразной пользуются аналогией с известными учащимся примерами взаимно обратных операций. Например, операция сложения позволяет по двум данным числам найти третье число - их сумму. Если же известно первое слагаемое и сумма, то второе слагаемое может быть "восстановлено" выполнением операции вычитания. Следовательно, вычитание - операция, обратная сложению, приводящая к единственному результату. Однако такое бывает не всегда. Например, возведение в квадрат числа 3 дает число 9. Пусть теперь известно, что число 9 является квадратом некоторого числа. Выполнив обратную операцию - извлечение квадратного корня - получаем два значения: 3 и -3. Дифференцирование функции приводит к новой функции, которая является производной функции Пусть теперь известно, что производная некоторой функции равна, т.е. требуется найти функцию. Операция нахождения функции по ее производной называется интегрированием. Выполняя интегрирование, можем получать следующие результаты: и т.д. Функция называется первообразными функции. Таким образом, интегрирование является операцией, обратной дифференцированию; результат операции интегрирования называется первообразной. После этого сообщается определение первообразной: функция называется первообразной для функции f(x) на заданном промежутке, если для всех x из этого промежутка. Перечисленные понятия вводятся на дедуктивной основе, дается иллюстрация использования определения основного понятия, его свойств с помощью конкретных примеров.

---

9. 
   Методика введения определения sin, cos, tg, где, а принадлежит R.
   
10. 
    Методика изучения тригонометрических функций числового аргумента.
    

Введение тригонометрических функций начинается в старшей школе с введения элементарных понятий: числовая окружность, числовая окружность на координатной плоскости, определения синуса и косинуса числа, основное тригонометрическое тождество, определение тангенса и котангенса, тригонометрические функции числового аргумента, числовые функции углового аргумента, формулы приведения.

И только после этого рассматривают функцию y=sin x, свойства и график.

Свойства:

1. 
   D(y)=R
   
2. 
   y=sin x – нечётная
   
3. 
   y=sin x возрастает на [0;П/2], убывает на [П/2;П]
   
4. 
   ограничена снизу и сверху
   
5. 
   у_наим=-1, у_наиб=1
   

По этим свойствам строим график, таблично на [0;П], используя свойство симметричности на остальном графике.



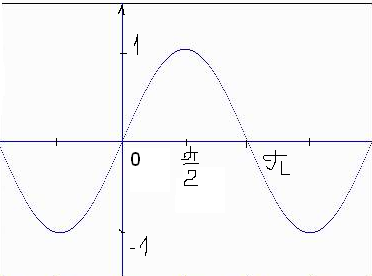
После построения: непрерывность

В таком же порядке рассматриваем функцию y=cos x.

Опр: Функцию f(x),xєX называют периодической, если сущ. Т≠0, что для любого xєX выполняется f(x-T)=f(x+T), T – период функции f(x), значит функции y=sin x, y=cos x – периодические.

sin(x-2П)=sinx=sin(x+2П)

cos(x+2П)=sinx= sin(x-2П), 2П – период функций y=sin x, y=cos x. Периодом является любое число вида kT, где k=±1;±2;±3…

T – наименьший положительный период, нахождение Т по определению.

Пример: Найти период функции y=sin 3x.

Решение: Пусть Т – основной период

f(x)=f(x+T)

f(x)=sin(x)

f(x+T)=sin 3(x+T)=sin (3x+3T)

sin 3x=sin (3x+3T)→3T=2Пn, т.к. нужен основной период n=1

3T=2П, Т=2П/3

Основной период функции y=sin kx (y=cos kx) равен 2П/k.

После изучения функций y=sin x , y=cos x знакомятся с преобразованием графиков функции y=f(x), y=mf(x), y=f(kx).

Далее знакомятся с функциями y=tg x, y=ctg x.

Тригонометрии в школе традиционно уделяется много внимания - сначала в курсе геометрии, затем в курсе алгебры и начал анализа. А.Г.Мордкович предлагает построить изучение темы «Тригонометрия» по следующей схеме: функция – уравнения – преобразования. Объясняется это тем, что сначала целесообразно изучить «простые модели» (таковыми являются элементарные функции), а затем переходить к изучению «сложных моделей» (таковыми в математике являются сложные выражения

---

, которые нужно упрощать, используя формульный аппарат). Таким образом, изучение данной темы следует построить по следующей схеме: 1. рассмотрение тригонометрической формы записи действительного числа и ее свойств. Основной целью является изучить новые математические модели – числовую окружность и числовую окружность на координатной плоскости; познакомить учащихся с первым классом неалгебраических функций – тригонометрическими функциями; научить школьников находить значение тригонометрических функций некоторого аргумента по известному значению другой функции того же аргумента; дать представление о градусной и радианной мерах измерения углов. 2. Собственно тригонометрические уравнения. Основная цель – научить школьников решать простейшие тригонометрические уравнения. Сначала надо разобраться с «элементарными моделями», т.е. с простейшими тригонометрическими уравнениями и уравнениями, которые сводятся к простейшим с помощью алгебраических приемов, и только потом переходить к «сложным моделям», т.е. к уравнениям, которые надо сначала долго и упорно «раскручивать, используя рутинный аппарат формул». 3. Тригонометрическими формулами следует заняться после того, как учащиеся овладеют двумя «китами», на которых базируется курс тригонометрии: числовой окружностью и простейшими уравнениями. Основная цель – познакомить учащихся с основными тригонометрическими формулами, научить находить нужную формулу для доказательства тригонометрических тождеств, упрощения тригонометрических выражений. После того, как пройдена тема «Простейшие тригонометрические уравнения», учащимся предлагаются задания с использованием формул тригонометрии. Отсюда и вытекает для учащихся польза от изучения формул: «жуткие» уравнения принимают после преобразований вполне знакомый вид.

Согласно стандарту полного общего образования в теме «Основы тригонометрии» должны быть рассмотрены следующие темы: синус, косинус, тангенс, котангенс произвольного угла; радианная мера угла; синус, косинус, тангенс, котангенс числа; основные тригонометрические тождества; формулы привидения; синус, косинус, тангенс суммы и разности двух углов; синус, косинус двойного угла; формулы половинного угла; преобразование суммы тригонометрических функций в произведение и произведения в сумму; выражение тригонометрических функций через тангенс половинного аргумента; преобразование простейших тригонометрических выражений; простейшие тригонометрические уравнения; решение тригонометрических уравнений; простейшие тригонометрические неравенства; арксинус, арккосинус, арктангенс числа; тригонометрические функции, их свойства и графики, периодичность, основной период.

---

11. 
    Методика изучения показательной и логарифмической функций.
    

Ознакомление учащихся с показательной и логарифмической функциями начиная с изучения свойств степеней и логарифмов.

Курс алгебры знакомит учащихся с понятием степени с рациональным показателем. Таким образом для любого основания степени 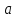(где 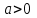, 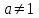) можно построить функцию: 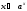, , 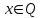область определения которой – множество действительных чисел. Необходимо ввести определение степени с иррациональным показателем. Используемое свойство степени с основным, например, большим единицы (возрастании), рациональное приближение иррационального числа α: r₁< α< r₂. Исходя из графического изображения зависимости показателя степени и значения степени, показывается, что найдется такое значение y, которое будет наибольшим среди всех a^r1 и наименьшим среди всех a^r2 , которое можно считать значением a^α.

Затем формируется определение показательной функции: функция, заданная формулой y=a^x ( 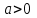, 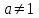), называется показательной функцией с основанием a, и формулируемые основные свойства: D(a^x)=R; E(a^x)=R_Т; a^x возрастает при a>1 и a^x убывает при 0
Логарифмическая функция – новый математический объект для учащихся. К понятию логарифма учащихся подводят в процессе решения показательного уравнения a^x=b в том случае, если b нельзя представить в виде степени с основанием a. Наше уравнение в случае b>0 имеет единственный корень, который называют логарифмом b по основанию a и обозначают log_ab, т.е. a^logab=b. Одновременно с введением нового понятия учащиеся знакомятся с основным Логарифмическим тождеством. При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции:

При любом (

---

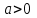Смотрите также файлы

• 2. 1 Моделирование бизнеспроцессов.docx

• Практическое задание 1 по учебному курсу Надзор и контроль в сфере безопасности.docx

• Программа внеурочной деятельности Разговоры о важном 1011 класс 35 часов Классный руководитель 11 А класса.docx

• Главный же вопрос данной статьи.docx

• Как неприятно бывает, когда над головой сгущаются тучи и появляется дождь, гроза или снег! Ненавистная погода может испортить настроение и планы на весь день.docx