Подходы к введению понятия производная:

1. 
   Логический (в классах с углубленным изучением математики): производная определяется через предел функции в точке.
   
2. 
   Исторический: производная определяется без использования понятия предела, поскольку в математике первоначально были сформированы понятия производной и интеграла, а затем, как обобщение данных понятий, понятие предела функции. Данный путь реализуется в классах общеобразовательного уровня.
   

Для рассмотрения примеров, приводящих к определению и применению данного понятия, необходимо актуализировать следующие элементы знаний: приращение аргумента, приращение функции, свойства графика линейной функции.

  Определение: Производной y ' =f ' (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т.е. конечен.
  Таким образом, 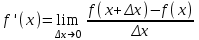, или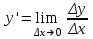

  Заметим, что если при некотором значении x, например при x=a, отношение 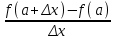при x0 не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a.

Возрастание и убывание функции. Экстремум функции.

  Определение 1. Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если f(x₂) > f(x₁) при x₂ > x₁.

  Из этого определения следует, что у возрастающей в интервале (a,b) функции f(x) в любой точке этого интервала приращения x и y имеют одинаковые знаки.
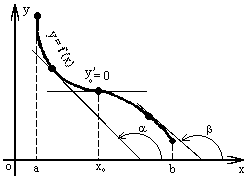    Определение 2. Функция f (x) называется убывающей в интервале ( a, b )

---

если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если f(x₂) < f(x₁) при x₂ > x₁.

  Из этого определения следует, что у убывающей в интервале ( a, b ) функции f (x) в любой точке этого интервала приращения x и y имеют разные знаки. 

Определение 3. Максимумом функции f (x) называется такое значение f (x₀) этой функции, которое не меньше всех значений

функции f (x) в точках x, достаточно близких к точке x₀ , т.е. в точках x,

  Значение f (x₀) функции f (x), при котором выполняется вышеуказанное неравенство, называется минимальным значением функции f (x) или просто минимумом.
  Определение 4. Минимумом функции f (x) называется такое значение f (x₀) этой функции, которое не больше всех значений функции f (x) в точках x, достаточно близких к точке x₀ , т.е. в точках x, принадлежащихнекоторой достаточно малой окрестности точки x₀ .

Геометрический смысл производной.

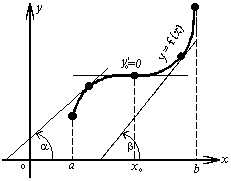
Рассмотрим график функции у = f (х), дифференцируемой в окрест­ностях точки x₀


f(x)


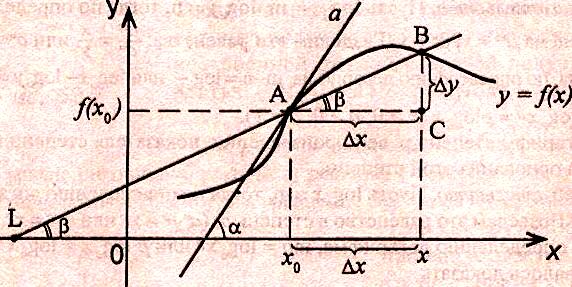
Рассмотрим произвольную прямую, проходящую через точку гра­фика функции - точку А(x₀, f (х₀)) и пересекающую график в некоторой точке B(x;f(x)). Такая прямая (АВ) называется секущей. Из ∆АВС: АС = ∆x; ВС =∆у; tgβ=∆y/∆x .

Так как АС || Ox, то ALO = BAC = β (как соответственные при параллельных). Но ALO - это угол наклона секущей АВ к положи­тельному направлению оси Ох. Значит, tgβ = k - угловой коэффициент прямой АВ.

Теперь будем уменьшать ∆х, т.е. ∆х→ 0. При этом точка В будет прибли­жаться к точке А по графику, а секущая АВ будет поворачиваться. Пре­дельным положением секущей АВ при ∆х→ 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А.

Если перейти к пределу при ∆х → 0 в равенстве tgβ =∆y/∆x, то получим 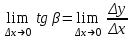или tg =f '(x₀), так как 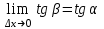-угол накло­на касательной к положительному направлению оси Ох

---

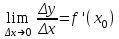, по определению производной. Но tg = k - угловой коэффициент каса­тельной, значит, k = tg = f '(x₀).

Итак, геометрический смысл производной заключается в следую­щем:

Производная функции в точке x₀ равна угловому коэффициенту ка­сательной к графику функции, проведенной в точке с абсциссой x₀.

Физический смысл производной.

Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени [t₀; t₀+ ∆t] равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е.

Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0.

lim Vср (t) = (t₀) - мгновенная скорость в момент времени t₀, ∆t → 0.

а lim = ∆x/∆t = x'(t₀) (по определению производной).

Итак, (t) =x'(t).

Физический смысл производной заключается в следующем: произ­водная функции y = f(x) в точке x₀ - это скорость изменения функции f (х) в точке x₀

Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.

(t) = x'(t) - скорость,

a(f) = '(t) - ускорение, или

a(t) = x"(t).

Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращатель­ном движении:

φ = φ(t) - изменение угла от времени,

ω = φ'(t) - угловая скорость,

ε = φ'(t) - угловое ускорение, или ε = φ"(t).

Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:

m = m(х) - масса,

x  [0; l], l - длина стержня,

р = m'(х) - линейная плотность.

С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука

F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω² =k/m, получим дифференциальное уравнение пружинного маятника х"(t) + ω²x(t) = 0,

где ω = √k/√m частота колебаний (l/c), k - жесткость пружины (H/m).

Уравнение вида у" + ω²y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решени­ем таких уравнений является функция

у = Asin(ωt + φ₀) или у = Acos(ωt + φ₀), где

А - амплитуда колебаний, ω - циклическая частота,

---

φ₀ - начальная фаза.

5. 
   Общая схема исследования функции. Применение производной при исследовании функции.
   
6. 
   Понятие математического моделирования. Применение производной для нахождения наибольшего и наименьшего значения функции.
   
7. 
   Методика введения первообразной. Методика нахождения первообразных.
   

Теме «Первообразная» предшествует тема «Первообразная и ее применение». Такая последовательность изучения материала создает предпосылки для

1. 
   понимания учениками взаимосвязи между операциями дифференцирования и интегрирования функций, а также основной идеи метода дифференциального и интегрального исчислений (зная функцию, можно установить характер локальной ее изменяемости в зависимости от изменения аргумента, и наоборот6 зная характер локальной изменяемости функции, можно найти либо саму функцию (при заданных начальных условиях), либо семейство функций;
   
2. 
   осознания обучающимися того факта, что аппарат производной и интеграла – основа метода математического анализа: он выступает и как язык, описывающий многие явления, процессы мира, и как инструмент, с помощью которого с учетом особенностей языка исследуются эти явления и процессы.
   

При рассмотрении элементов интегрального исчисления реализуется идея линеаризации. С точки зрения механики скорость прямолинейного движения определяется как производная пути по времени. Если теперь рассмотреть обратную задачу – нахождения пути, пройденного точкой с заданной скоростью, то придем к функции, которую называют первообразной к исходной функции. Так как производная постоянной равна нулю, то первообразная определяется с точностью до постоянной.

Если скорость меняется по закону v = v(t) и ее графиком является некоторая кривая, то путь, пройденный точкой за промежуток времени [t; t + h], приближенно равен площади прямоугольника со сторонами v(t) и h. Точное значение пути будет равно площади образовавшейся криволинейной трапеции. Если в заданную кривую v(t) вписать некоторую ломаную, то путь можно вычислить с лучшим приближением, заменив площадь криволинейной трапеции суммой площадей прямоугольников разбиения. Чем меньше будет основание прямоугольников, тем ближе сумма их площадей будет выражать площадь криволинейной трапеции. Так процесс линеаризации приводит к понятию определенного интеграла.

---

Учебный материал строится так, что вначале вводится понятие первообразной. Таблица первообразных получается из таблицы производных. В курсе математики средней школы нет понятия неопределенного интеграла (хотя в учебнике А.Г. Мордковича этот термин используется), поэтому определенный интеграл называют просто интегралом. Введение понятия определенного интеграла осуществляется в виде предела интегральных сумм. Интегральная сумма рассматривается в общем виде (отрезки разбиения могут быть необязательно равными) и предназначена только для ознакомления с понятием интеграла. Желательно, чтобы ученики понимали, что об интегральной сумме функции на отрезке, а затем и интеграле можно говорить и в том случае, когда функция не только непрерывна и положительна, но и принимает на этом отрезке любые значения, в том числе и отрицательные, и ноль. Формула Ньютона – Лейбница вводится практически одновременно с термином «интеграл». Эта формула является главной: с ее помощью вычисляются определенные интегралы.

Центральное место во всем разделе, связанном с изучением элементов интегрального исчисления, занимает вычисление площадей плоских фигур. Основной фигурой считается криволинейная трапеция. При изучении этого материала важно правильно расставлять акценты: главное здесь – построение геометрических моделей и снятие соответствующей информации с чертежа, а не вычисление интегралов. Не ради изучения интеграла считаются площади, наоборот, интеграл изучается ради вычисления площадей.

8. 
   Методика введения интеграла. Применение интеграла для вычисления площадей и объемов.
   

Основная образовательная цель изучения темы "Первообразная и интеграл" может быть сформулирована так:

1) ознакомить учащихся с операцией, которая является обратной по отношению к операции дифференцирования функций;

2) познакомить с использованием метода интегрального исчисления для решения геометрических задач, некоторых задач практического содержания.

В связи с этим развивающими целями будут:

а) введение нового метода решения задач (в частности нахождение площади объёма фигуры) показать известную универсальность математических методов;

б) показ учащимся основных этапов решения прикладных задач средствами математики.

Теме "Первообразная и интеграл" предшествует тема "Производная и её применение". Такая последовательность изучения материала создаёт предпосылки для:

---

Смотрите также файлы

• 2. 1 Моделирование бизнеспроцессов.docx

• Практическое задание 1 по учебному курсу Надзор и контроль в сфере безопасности.docx

• Программа внеурочной деятельности Разговоры о важном 1011 класс 35 часов Классный руководитель 11 А класса.docx

• Главный же вопрос данной статьи.docx

• Как неприятно бывает, когда над головой сгущаются тучи и появляется дождь, гроза или снег! Ненавистная погода может испортить настроение и планы на весь день.docx