Файл: Методические рекомендации по выполнению контрольной работы по дисциплине Математика.docx
Добавлен: 03.12.2023
Просмотров: 137
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приложение 6
к рабочей программе
Федеральное государственное бюджетное образовательное учреждение высшего образования
УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ
УТВЕРЖДЕНЫ
на заседании кафедры шахматного искусства и компьютерной математики
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ
по дисциплине
Математика
Прежде чем приступить к выполнению контрольной работы необходимо ознакомиться с теоретическим материалом. Рекомендуется также изучить Методические указания к решению задач (в конце данного пособия). Выбор варианта осуществляется с приведенной ниже таблицей. Работу следует сдать на проверку не позднее, чем за 3 дня до зачета/экзамена. Проверенная работа может быть возвращена на доработку. В этом случае студент выполняет работу над ошибками и сдает работу повторно.
Важно: работу следует загружать одним файлом (или архивом)
Рекомендации по изучению разделов и тем дисциплины
Тема 1. Введение в математический анализ.
Необходимо добросовестно освоить, уточнить, запомнить понятие множества, операции над множеством, логическую символику, обозначения, чтобы Вы могли понимать преподавателя.
Обратите внимание на следующие понятия: простейшие и элементарные функции; способы задания функции; числовая последовательность; монотонность, ограниченность последовательности; пределы функций; правила раскрытия неопределенностей при вычислении пределов.
Понятие предела являются основными в современной математике. При самостоятельной работе по данной теме следует основательно отработать технику вычисления предела, приемы раскрытия неопределенностей.
Тема 2. Основы дифференциального и интегрального исчислений функций одной переменной.
Понятие производной и предела являются основными в современной математике. Запомнить таблицу основных производных. Уметь вычислять производные сложных функций. Теория одного раздела курса используется во многих прикладных задачах экономики.
Понятие первообразной и интеграла дополняют понятия производной и дифференциала. Ввиду этого студенту необходимы прочные знания дифференциального исчисления. Нужно иметь навыки выполнения преобразований элементарных функций. При самостоятельной работе по данной теме следует основательно отработать технику вычисления интегралов различного типа. Обратите внимание на особенности вычисления определенных интегралов, поскольку в понятия определенного интеграла присутствуют важнейшие математические операции: сумма и предел.
Тема 3. Функции нескольких переменных.
Рекомендуется обратить внимание на изучение понятий: частные производные, их геометрический смысл, градиент поля, полный дифференциал, свойство смешанных производных, экстремума функции двух переменных.
Тема 4 Элементы линейной алгебры и аналитической геометрии.
Все понятия, которые рассматриваются в рамках этой темы, являются необходимыми при изучении дисциплины. Обратите внимание на следующие понятия: скалярные величины, вектор, матрица; определитель, минор; система линейных уравнений; система линейных неравенств.
Рекомендуется обратить внимание на изучение тем: Прямая на плоскости. Виды уравнения прямой на плоскости. Взаимное расположение двух прямых на плоскости. Уравнения плоскости. Взаимное расположение плоскостей. Прямая в пространстве. Плоскость и прямая в пространстве.
Тема 5 Методы оптимальных решений.
Изучение этой темы начинают с изучения составления математических моделей. Особое внимание необходимо уделить графическому методу решения задач линейного программирования, алгоритму в решении задач симплексным методом.
Тема 6 Основы теории вероятностей.
При изучении случайных событий необходимо усвоить следующее:
элементарное событие; вероятностное пространство; достоверное событие, невозможное событие, случайное событие; основные комбинаторные схемы и правила; классический способ подсчета вероятности; дискретная вероятностная схема; геометрическая вероятность; несобственные события; зависимые и независимые события; условная вероятность; формула полной вероятности и формула Байеса; схема независимых испытаний Бернулли.
При изучении случайных величин необходимо осознанно усвоить следующие понятия: случайная величина; закон распределения случайных величин; функция распределения случайной величины; дискретные и непрерывные случайные величины; плотность распределения случайной величины; числовые характеристики случайной величины; случайный процесс.
При изучении случайных величин необходимо повторить дифференциальное и интегральное исчисление
, поскольку оно существенно используется при нахождении числовых характеристик непрерывной случайной величины. Следует обратить особое внимание на нормальное распределение, которое играет важную роль в математической статистике.
ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА
1 семестр
В каждомзаданииуказываетсяномерварианта (всего 10 вариантов).
Каждыйстудентвыполняетсвойвариант.
Выбор вариантов
| Начальные буквы фамилий студентов | Вариант |
| А, Б В, Г Д, Е, Ж З, И, К, Л, М Н, О, П Р, С Т, У, Ф, Х Ц, Ч, Ш, Щ Э, Ю, Я | 1 2 3 4 5 6 7 8 9 10 |
1. Вычислить пределы.
Вариант 1. а)
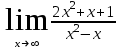 б)
б)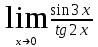 в)
в)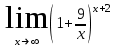
Вариант 2. а)
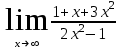 б)
б)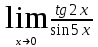 в)
в)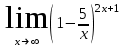
Вариант 3. а)
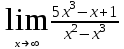 б)
б)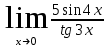 в)
в)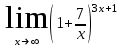
Вариант 4. а)
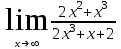 б)
б)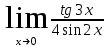 в)
в)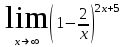
Вариант 5. а)
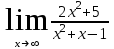 б)
б)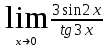 в)
в)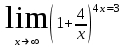
Вариант 6. а)
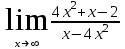 б)
б)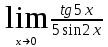 в)
в)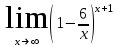
Вариант 7. а)
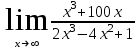 б)
б)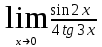
в)
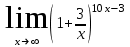
Вариант 8. а)
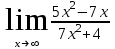 б)
б)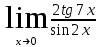 в)
в)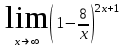
Вариант 9. а)
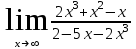 б)
б)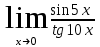 в)
в)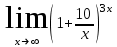
Вариант 10 а)
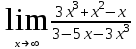 б)
б)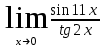 в)
в)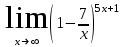
2. Найти первую производную функции:
Вариант 1. y=(2x-1)ln(2x+5)
Вариант 2. y=(7x+2)ln(x-2)
Вариант 3. y=(5x-3)ln(4x-1)
Вариант 4. y=(3x+5)ln(2x-7)
Вариант 5. y=(4x-1)ln(5x-1)
Вариант 6. y=(7x-1)ln(4x-1)
Вариант 7. y=(2x+3)ln(2x+3)
Вариант 8. y=(4x+10)ln(2x-7)
Вариант 9. y=(3x-4)ln(5x-1)
Вариант 10. у= (2x+5)ln(7x-5)
3. Найти неопределенный интеграл:
Вариант 1. а)
Вариант 2. а)
Вариант 3. а)
Вариант 4. а)
Вариант 5. а)
б)
Вариант 6. а)
Вариант 7. а)
Вариант 8. а)
Вариант 9. а)
Вариант 10. а)
4. Вычислить определенный интеграл:
Вариант 1. а)
 ; б)
; б) Вариант 2. а)
 ; б)
; б)  .
.Вариант 3. а)
