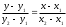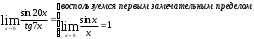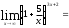Файл: Методические рекомендации по выполнению контрольной работы по дисциплине Математика.docx
Добавлен: 03.12.2023
Просмотров: 143
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; б)  .
.
Вариант 4. а) ; б)
; б)  .
.
Вариант 5. а) ; б)
; б) 
Вариант 6. а) ; б)
; б)  .
.
Вариант 7. а) ; б)
; б) 
Вариант 8. а) ; б)
; б)  .
.
Вариант 9. а) ; б)
; б)  .
.
Вариант 10. а) ; б)
; б)  .
.
5. Решить систему уравнений:
а) методом Крамера,
б) методом Гаусса
6. По координатам вершин треугольника ABC найти:
Сделать чертеж.
Вариант 1. А(1;2); В(-1;2); С(3;0).
Вариант 2. А(3;3); В(-3;-3); С(3;5).
Вариант 3. А(-1;1); В(5;1); С(3;7).
Вариант 4. А(3;1); В(3;-5); С(-1;-1).
Вариант 5. А(0;5); В(5;0); С(9;3).
Вариант 6. А(0;0); В(8;2); С(-2;6).
Вариант 7. А(-1;4) В(-1;2); С(-7;3).
Вариант 8. А(2;-1); В(5;3); С(5;-2).
Вариант 9. А(3;-3); В(7;-3); С(5;5).
Вариант 10. А(9;0); В(5;5); С(0;3).
Методические указания к решению задач
1. Вычислить пределы:
а)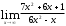
б)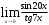
в)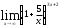
г)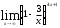
д)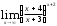
Решение:
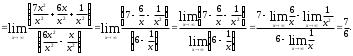
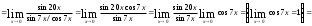
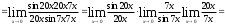
=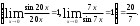
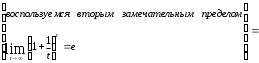
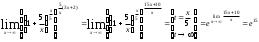
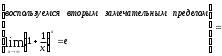
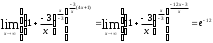
=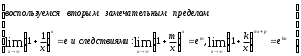 =
=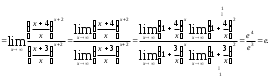
2. Найти первые производные функций:
а)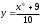
б)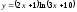
Решение:
а) Имеем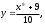
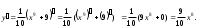
б)
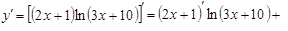
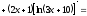
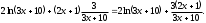
3. Вычислить неопределенные интегралы:
а)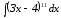 ; б)
; б) 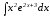 ; в)
; в) 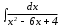 г)
г) 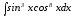
Решение:
а)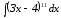
Сделаем замену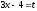 , отсюда
, отсюда 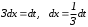
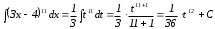
Возвратившись к старой переменной, имеем
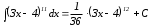
б)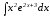
Интегрируем «по частям»: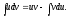
Пусть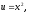 тогда
тогда 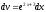
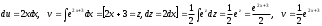 ,
,
Имеем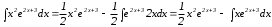
Интеграл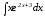 вычислим, снова применяя формулу интегрирования по частям.
вычислим, снова применяя формулу интегрирования по частям.
Пусть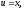 тогда
тогда 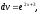
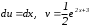
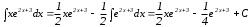
Таким образом, исходный интеграл равен
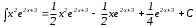
в)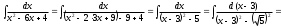
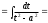
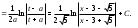
г)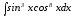
Полагая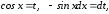 получим
получим
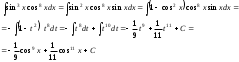
4. Вычислить определенные интегралы.
а)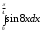 б)
б) 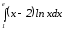 в)
в) 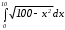
Решение:
а)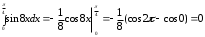
б)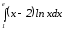
Интегрируем «по частям»
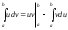
Пусть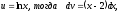
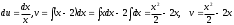 .
.
Имеем:
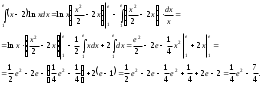
в)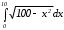
Интегрируем подстановкой.
Положим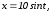 тогда
тогда 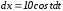 . Если
. Если 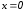 , то
, то 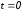 ; если
; если 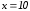 , то
, то 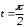 .
.
Поэтому
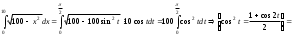
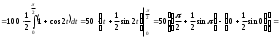
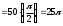 .
.
Заметим, что геометрически данный интеграл есть площадь круга: x2 + y2 ≤ 100, 0 ≤ x ≤ 10, 0 ≤ y ≤ 10.

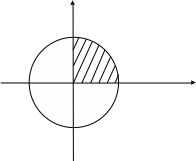
10



10
0
x
5. Решить систему уравнений:
а) методом Крамера,
б) методом Гаусса
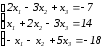
Решение:
а) Метод Крамера.
Найдем определители:
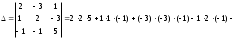
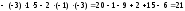
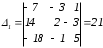 ,
, 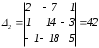 ,
, 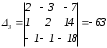
Теперь находим x1, x2 и x3:
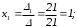
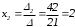 ;
; 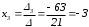 ;
;
Итак,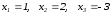
б) Метод Гаусса.
Составим расширенную матрицу системы и путем элементарных преобразований приведем данную матрицу системы к треугольному виду (под главной диагональю нули).
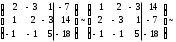

(для упрощения вычислений поменяем
местами 1-ю и 2-ю строки;
умножим 1-ю строку на -2 и прибавим ко 2-ой строке,
1-ю строку прибавим к 3-ей строке)
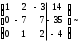
(2-е уравнение разделим на -7)
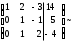
(2-ю строку умножим на -1 и прибавим к 3-ей строке)
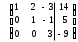
Таким образом, исходная система может быть представлена в виде:
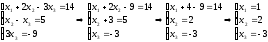
 Итак, х1=1, х1=2, х1=-3.
Итак, х1=1, х1=2, х1=-3.
6. Треугольник задан вершинами А (1;1); В (-2;1); С (-1;6).Найти:
в) угол ABC;
г) площадь треугольника.
Сделать чертеж.
Решение:
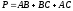 .
.
Длины сторон найдем по формуле расстояния между двумя точками:
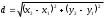
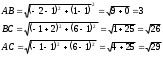
Итак, периметр треугольника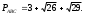
Вариант 4. а)
 ; б)
; б) Вариант 5. а)
 ; б)
; б) Вариант 6. а)
 ; б)
; б) Вариант 7. а)
 ; б)
; б) Вариант 8. а)
 ; б)
; б) Вариант 9. а)
 ; б)
; б)  .
.Вариант 10. а)
 ; б)
; б) 5. Решить систему уравнений:
а) методом Крамера,
б) методом Гаусса
| Вариант 1. 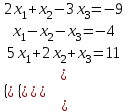 | Вариант 6. 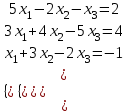 |
| Вариант 2. 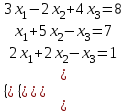 | Вариант 7. 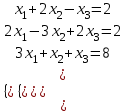 |
| Вариант 3. 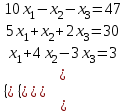 | Вариант 8. 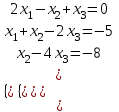 |
| Вариант 4. 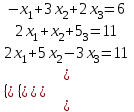 | Вариант 9. 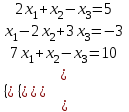 |
| Вариант 5. 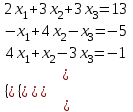 | Вариант 10. 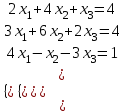 |
6. По координатам вершин треугольника ABC найти:
-
периметр треугольника; -
уравнения сторон AB и BC; уравнение высоты AD.
Сделать чертеж.
Вариант 1. А(1;2); В(-1;2); С(3;0).
Вариант 2. А(3;3); В(-3;-3); С(3;5).
Вариант 3. А(-1;1); В(5;1); С(3;7).
Вариант 4. А(3;1); В(3;-5); С(-1;-1).
Вариант 5. А(0;5); В(5;0); С(9;3).
Вариант 6. А(0;0); В(8;2); С(-2;6).
Вариант 7. А(-1;4) В(-1;2); С(-7;3).
Вариант 8. А(2;-1); В(5;3); С(5;-2).
Вариант 9. А(3;-3); В(7;-3); С(5;5).
Вариант 10. А(9;0); В(5;5); С(0;3).
Методические указания к решению задач
1. Вычислить пределы:
а)
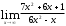
б)
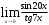
в)
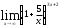
г)
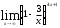
д)
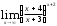
Решение:
-
Имеем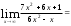 (разделим числитель и знаменатель на старшую степень)
(разделим числитель и знаменатель на старшую степень)
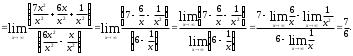
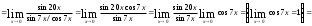
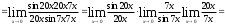
=
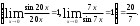
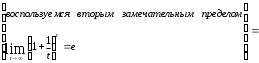
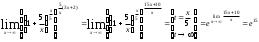
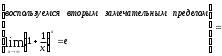
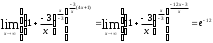
=
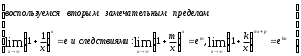 =
=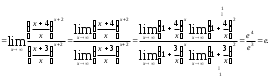
2. Найти первые производные функций:
а)
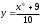
б)
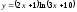
Решение:
а) Имеем
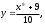
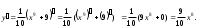
б)
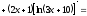
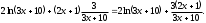
3. Вычислить неопределенные интегралы:
а)
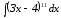 ; б)
; б) 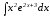 ; в)
; в) 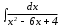 г)
г) 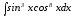
Решение:
а)
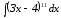
Сделаем замену
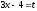 , отсюда
, отсюда 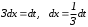
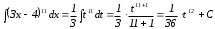
Возвратившись к старой переменной, имеем
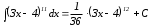
б)
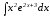
Интегрируем «по частям»:
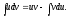
Пусть
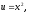 тогда
тогда 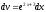
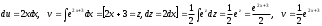 ,
, Имеем
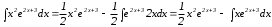
Интеграл
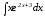 вычислим, снова применяя формулу интегрирования по частям.
вычислим, снова применяя формулу интегрирования по частям.Пусть
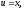 тогда
тогда 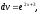
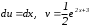
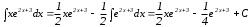
Таким образом, исходный интеграл равен
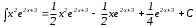
в)
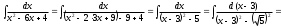
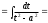
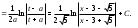
г)
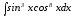
Полагая
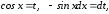 получим
получим 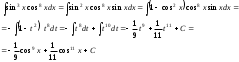
4. Вычислить определенные интегралы.
а)
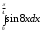 б)
б) 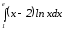 в)
в) 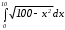
Решение:
а)
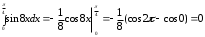
б)
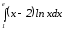
Интегрируем «по частям»
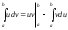
Пусть
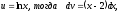
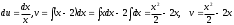 .
.Имеем:
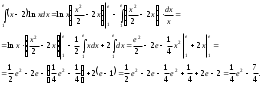
в)
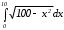
Интегрируем подстановкой.
Положим
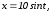 тогда
тогда 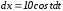 . Если
. Если 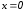 , то
, то 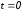 ; если
; если 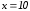 , то
, то 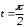 .
.Поэтому
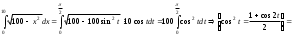
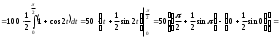
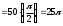 .
.Заметим, что геометрически данный интеграл есть площадь круга: x2 + y2 ≤ 100, 0 ≤ x ≤ 10, 0 ≤ y ≤ 10.


10



10
0
x
5. Решить систему уравнений:
а) методом Крамера,
б) методом Гаусса
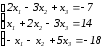
Решение:
а) Метод Крамера.
Найдем определители:
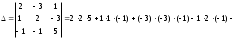
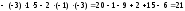
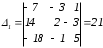 ,
, 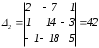 ,
, 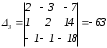
Теперь находим x1, x2 и x3:
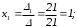
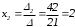 ;
; 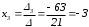 ;
; Итак,
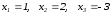
б) Метод Гаусса.
Составим расширенную матрицу системы и путем элементарных преобразований приведем данную матрицу системы к треугольному виду (под главной диагональю нули).
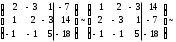

(для упрощения вычислений поменяем
местами 1-ю и 2-ю строки;
умножим 1-ю строку на -2 и прибавим ко 2-ой строке,
1-ю строку прибавим к 3-ей строке)
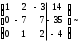
(2-е уравнение разделим на -7)
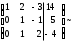
(2-ю строку умножим на -1 и прибавим к 3-ей строке)
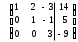
Таким образом, исходная система может быть представлена в виде:
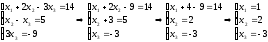
 Итак, х1=1, х1=2, х1=-3.
Итак, х1=1, х1=2, х1=-3.6. Треугольник задан вершинами А (1;1); В (-2;1); С (-1;6).Найти:
-
периметр треугольника; -
уравнения сторон треугольника; уравнение высоты AD.
в) угол ABC;
г) площадь треугольника.
Сделать чертеж.
Решение:
-
Для нахождения периметра P применим формулу:
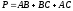 .
.Длины сторон найдем по формуле расстояния между двумя точками:
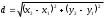
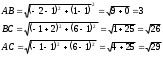
Итак, периметр треугольника
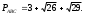
-
Для отыскания уравнений сторон треугольника используем уравнение прямой, проходящей через две данные точки М1(х1;у1) и М2(х2;у2):