ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 176
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра физических методов в прикладных исследованиях
Ю.Ф. Наседкина, Б.М. Костишко
КВАНТОВАЯ ОПТИКА
Учебно-методическое пособие
к лабораторным работам
Ульяновск
2017
УДК 537
ББК 22.33 я73
Н 31
Печатается по решению Ученого совета
инженерно-физического факультета высоких технологий
Ульяновского государственного университета
Рецензенты:
В.А. Кокин, кандидат педагогических наук, доцент УлГПУ;
А.А. Соловьев, кандидат физико-математических наук, доцент УлГУ
Наседкина Ю.Ф., Костишко Б.М.
Н 31 Квантовая оптика : учебно-методическое пособие. Квантовая оптика / Ю. Ф. Наседкина, Б.М. Костишко. – Ульяновск : УлГУ, 2017. – 76 с.
Пособие составлено в соответствии с рабочей программой курса «Физика» специальности «Компьютерная безопасность» ФМИАТ и включает в себя описание шести лабораторных работ. Каждая работа снабжена теоретическим введением, подробным описанием эксперимента, а также контрольными вопросами, призванными помочь самостоятельному освоению материала студентами.
УДК 537
ББК 22.33 я73
Директор Издательского центра Т.В. Филиппова
Редактирование и подготовка оригинал-макета __
Подписано в печать.
Формат 60х84/16. Усл. печ. л. 4,4. Уч.-изд. л. 3,8.
Тираж 100 экз. Заказ __
Оригинал-макет подготовлен
В Издательском центре
Ульяновского государственного университета
Отпечатано в Издательском центре
Ульяновского государственного университета
432000, г. Ульяновск, ул. Л. Толстого, 42

© Наседкина Ю.Ф., Костишко Б.М., 2017
© Ульяновский государственный университет, 2017
Содержание
Лабораторная работа 1. Эффект Комптона 4
Лабораторная работа 2. Опыт Франка и Герца 10
Лабораторная работа 3. Фотоэффект 18
Лабораторная работа 4. Изучение спектра атома водорода и определение постоянной Ридберга 29
Лабораторная работа 5. Изучение законов теплового излучения 35
Лабораторная работа 6. Определение работы выхода электронов из металла 42
Литература 50
ЛАБОРАТОРНАЯ РАБОТА № 1
ЭФФЕКТ КОМПТОНА
ЦЕЛИ РАБОТЫ:
-
Знакомство с моделями электромагнитного излучения и их использованием при анализе процесса рассеяния рентгеновского излучения на веществе.
-
Экспериментальное подтверждение закономерностей эффекта Комптона.
-
Экспериментальное определение комптоновской длины волны электрона.
КРАТКАЯ ТЕОРИЯ
Когда волны отражаются или претерпевают дифракцию на препятствиях, их длина волны и частота остаются неизменными. Это следует из классической теории Джозефа Джона Томсона, в соответствии с которой под действием периодического электрического поля световой волны электроны вещества колеблются с частотой поля и, вследствие этого, излучают вторичные (рассеянные) волны той же частоты. Поэтому в 1922 г. немалое удивление вызвал опыт Комптона, показавший, что у рентгеновских лучей, рассеянных атомами, наряду с первоначальной частотой обнаруживается новая частота ω'=-ω. Такое рассеяние со сдвигом частоты (или длины волны ) называется эффектом Комптона. Более строго под эффектом Комптона понимается явление, сопровождающее рассеяние электромагнитного излучения на свободных (слабосвязанных) электронах атома, приводящее к изменению его частоты и длины волны. Поскольку величина (или ) весьма мала, эффект Комптона экспериментально наблюдается только для коротковолновых излучений – рентгеновских (10-8 >λ> 10−12 м) или гамма-лучей (λ<10-11 м), для которых относительное изменение частоты оказывается существенным. Результаты этого опыта можно объяснить, только предположив, что электромагнитное излучение проявляет корпускулярные свойства и представляет собой поток частиц – фотонов. Фотоны обладают импульсом, и их взаимодействие с электронами вещества происходит подобно сталкивающимся шарам по законам абсолютно упругого соударения.
Эффект Комптона - упругое рассеяние монохроматического электромагнитного излучения на свободных электронах, сопровождающееся увеличением длины волны. За проведенные эксперименты и истолкование их результатов в 1927 г. американский физик Артур Комптон был удостоен Нобелевской премии.
Формула Комптона, определяющая изменение длины волны рассеянного излучения, имеет вид:
Знакомство с моделями электромагнитного излучения и их использованием при анализе процесса рассеяния рентгеновского излучения на веществе.
Экспериментальное подтверждение закономерностей эффекта Комптона.
Экспериментальное определение комптоновской длины волны электрона.
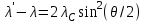 | | (1.1) |
где λ и
 - соответственно, длины волн до и после рассеяния; θ – угол рассеяния; λС - так называемая комптоновская длина волны электрона, равная λС = 2,4·10-12 м.
- соответственно, длины волн до и после рассеяния; θ – угол рассеяния; λС - так называемая комптоновская длина волны электрона, равная λС = 2,4·10-12 м.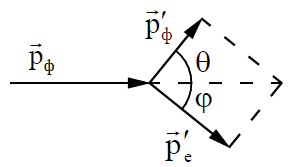
Рис.1.1. Схема комптоновского рассеяния
Эффект Комптона представлен на диаграмме рис. 1.1, иллюстрирующей закон сохранения импульса при упругом рассеянии фотонов на свободных электронах. До столкновения электрон покоится. Его импульс ре =0. После столкновения электрон отдачи имеет импульс
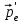 ;
; 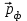 и
и 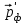 - импульс налетающего и рассеянного фотонов;
- импульс налетающего и рассеянного фотонов; 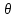 - угол рассеяния фотона; φ – угол, под которым летит электрон отдачи относительно направления падающего фотона (угол отдачи).
- угол рассеяния фотона; φ – угол, под которым летит электрон отдачи относительно направления падающего фотона (угол отдачи). В рентгеновском диапазоне длин волн и для гамма-излучения энергия фотонов соизмерима с собственной энергией электрона
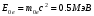 . Так как при рассеянии фотонов такой высокой энергии электрон может приобрести значительную кинетическую энергию, при рассмотрении эффекта Комптона необходимо использовать законы релятивистской механики.
. Так как при рассеянии фотонов такой высокой энергии электрон может приобрести значительную кинетическую энергию, при рассмотрении эффекта Комптона необходимо использовать законы релятивистской механики.Если
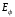 и
и 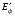 энергия фотона, а
энергия фотона, а 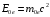 и
и 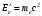 - энергия электрона, соответственно, до и после столкновения, то исходная система уравнений, описывающих упругое столкновение фотона со свободным электроном включает закон сохранения энергии
- энергия электрона, соответственно, до и после столкновения, то исходная система уравнений, описывающих упругое столкновение фотона со свободным электроном включает закон сохранения энергии 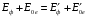 или или 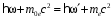 , , | | (1.2) |
где
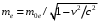
, и закон сохранения импульса (рис.1.1)
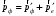 или или 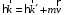 , , | | (1.3) |
где
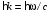 ,
,  . Для фотона как частицы с нулевой массой покоя энергия и импульс связаны соотношением
. Для фотона как частицы с нулевой массой покоя энергия и импульс связаны соотношением 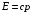 . Тогда закон сохранения примет вид
. Тогда закон сохранения примет вид 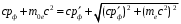 . . | | (1.4) |
Из закона сохранения импульса по теореме косинусов получим:
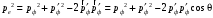 . . | | (1.5) |
Возведем в квадрат левую и правую часть закона сохранения энергии (1.4):
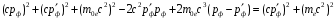 . . | | |
Учитывая (1.5) и упрощая выражение, запишем
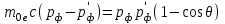 , или
, или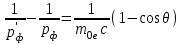 .
.Тогда, подставляя
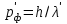 и
и 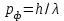 , имеем
, имеем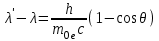 . (1.6)
. (1.6)Коэффициент
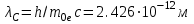 носит название комптоновской длины волны.
носит название комптоновской длины волны.МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ
-
Запустить программу Labvisual ФЯЛ-02. -
С помощью пульта управления установить необходимый угол измерения, при этом активный датчик отмечается световым сигналом. Выбрать удобную для измерения интенсивность сигнала.

Рис.1.2. Внешний вид установки «Наблюдение эффекта Комптона».
-
Пульт управления -
Регистрирующее устройство.
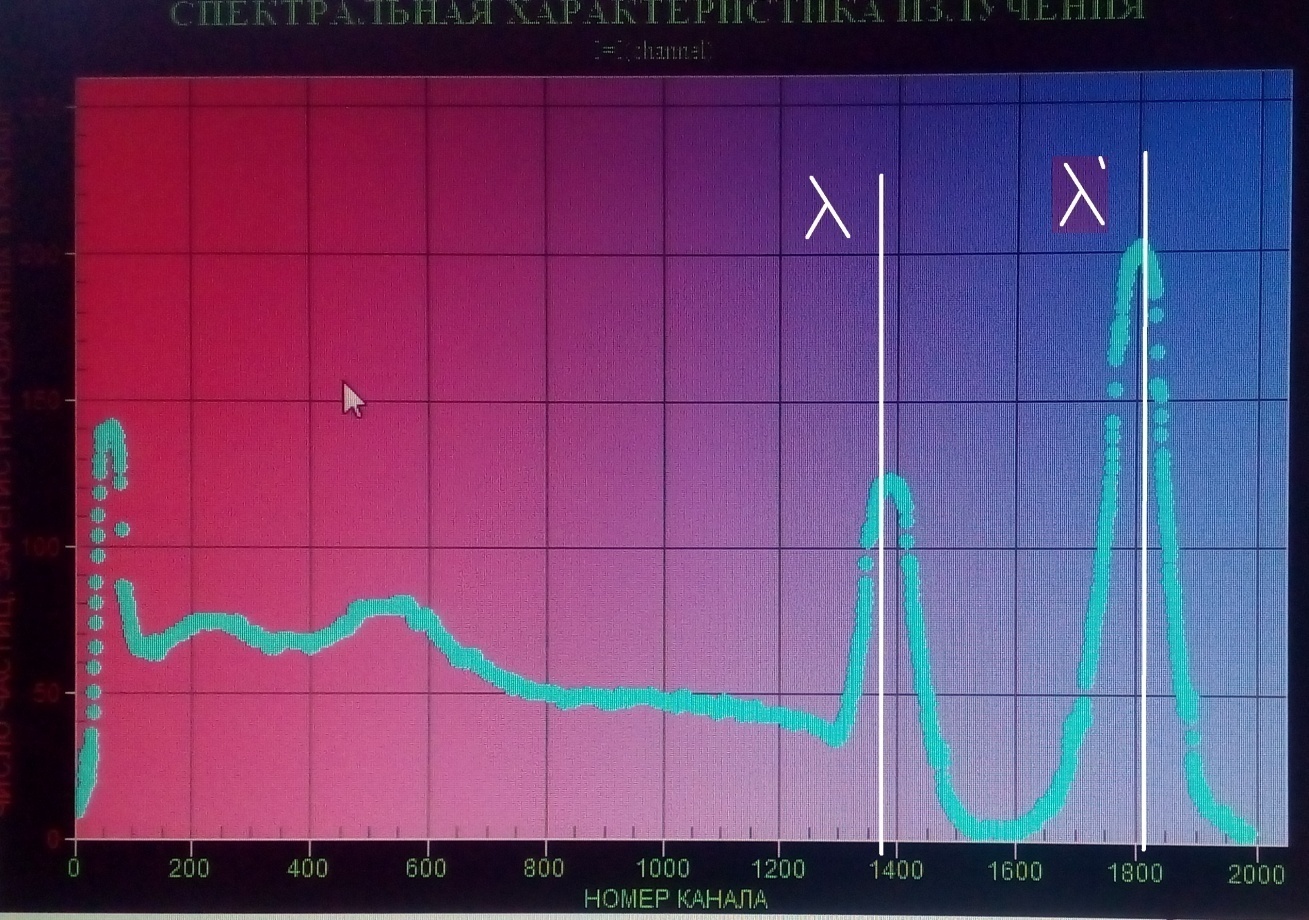
Рис. 1.3. Вид окна сканирования спектра.
Таблица 1.1.
| № | θ | (1-cosθ) | λ | 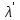 | λC | <λC> |
| 1 | 00 | | | | | |
| 2 | 100 | | | | | |
| 3 | 200 | | | | | |
| 4 | 300 | | | | | |
| 5 | 400 | | | | | |
| 6 | 500 | | | | | |
| 7 | 600 | | | | | |
| 8 | 700 | | | | | |
| 9 | 800 | | | | | |
| 10 | 900 | | | | |
-
В меню программы выбрать «Автоматическое сканирование и набор спектра». Нажать «Автоскан+» или «Автоскан-». Справа поставить флажок в окне «Показать набираемый спектр» и нажать «Визуализировать данные». -
Измерить длины волн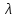 и
и 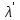 , как показано на рис.1.3. Заполнить соответствующую строку таблицы 1.1.
, как показано на рис.1.3. Заполнить соответствующую строку таблицы 1.1. -
Повторить пп.2-4 для других углов измерения, согласно Вашему варианту. -
Вычислить и записать в табл. 1.1 величины (1 – cos). Построить график зависимости изменения длины волны (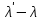 ) для каждой серии измерений.
) для каждой серии измерений. -
Определите по наклону графика значение комптоновской длины волны электрона
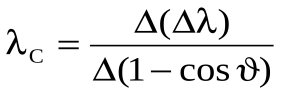 .
.Запишите результат и сделайте вывод.
Вопросы и задания для самоконтроля
-
Что означает «корпускулярно-волновой дуализм»? Опишите модели, с помощью которых описываются свойства квантовых частиц. -
Что такое луч? Что такое гармоническая волна? Сформулируйте связь между характеристиками электромагнитной волны в волновой и квантовой моделях. -
Опишите модель взаимодействия падающего рентгеновского фотона и свободного электрона вещества. Какие законы сохранения выполняются при взаимодействии фотона с электроном в эффекте Комптона? -
Сравните поведение фотонов после взаимодействия с электронами в эффекте Комптона и фотоэффекте. -
Что такое комптоновская длина волны частицы? -
Почему эффект Комптона не наблюдается при рассеянии фотонов на электронах, сильно связанных с ядром атома? -
Как меняется энергия фотона при его комптоновском рассеянии? Что происходит с электроном после рассеяния на нем фотона? -
Чем отличается масса частицы от массы покоя? Когда они совпадают? -
Напишите формулу импульса фотона. -
Изобразите чертеж взаимодействия фотона с электроном в эффекте Комптона. Выведите формулу (1.6). -
Напишите формулу для комптоновской длины волны электрона.
ЛАБОРАТОРНАЯ РАБОТА № 2
ОПЫТ ФРАНКА И ГЕРЦА
ЦЕЛЬ РАБОТЫ:
изучение процесса возбуждения атомов металла электронами, измерение первого потенциала возбуждения.
КРАТКАЯ ТЕОРИЯ
Еще в античные времена Демокрит высказал идею о том, что Вселенная состоит из маленьких неделимых частиц — атомов. Это представление о строении вещества сохранилось до конца XIX столетия, когда достоверно было установлено, что в состав каждого атома входят электроны. Приоритет в открытии электрона принадлежит английскому физику Джозефу Джону Томсону. Тогда же стало известно, что атом электрически нейтрален. Следовательно, отрицательный заряд электронов должен компенсироваться положительным зарядом неизвестных частиц, входящих в заряд атома.
В 90-х годах XIX века получила широкое распространение модель атома Томсона в виде однородной положительной сферической среды, в которой, как изюминки в булке, рассредоточены отрицательно заряженные электроны. Атомная модель Томсона подобна кексу. Однако вскоре автор «кексовой» модели высказал предположение о нестатическом положении электронов в атоме.