ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 181
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Установить на оптической скамье неоновую лампу в качестве источника излучения и отрегулировать одинаковую высоту источника и приемника излучения. -
Используя градуировочный график, выбрать и измерить длины волн семи наиболее ярких линий спектра неона. Результаты занести в таблицу 4.2.
Таблица 4.2. Наблюдение спектра неоновой лампы
№ | Цвет линии | Длины волн линий спектра неона λ, нм | Положение микрометрического винта d, мкм |
| 1 | | | |
| 2 | | | |
| 3 | | | |
| 4 | | | |
| 5 | | | |
| 6 | | | |
| 7 | | | |
Измерение постоянной Ридберга
-
Расположить на оптической скамье водородную лампу максимально близко к приемнику излучения и провести настройку с помощью регулировочных винтов. -
Определить длины волн трех линий серии Бальмера спектра атома водорода. С помощью формулы (4.8) рассчитать значение постоянной Ридберга. Заполнить таблицу 4.3.
Таблица 4.3. Измерение постоянной Ридберга
| Линия спектра | Градусные деления барабана | Длина волны | Квантовые числа | Постоянная Ридберга R | ||
| n | i | |||||
| Красная, 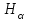 | | | 2 | 3 | | |
| Зелено-голубая, 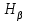 | | | 2 | 4 | | |
| Синяя, 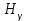 | | | 2 | 5 | | |
-
Определить среднее значение постоянной Ридберга и определить статистическую погрешность. Сопоставить полученное значение известным табличным значением R. Сформулировать вывод по работе.
Вопросы и задания для самоконтроля
1. Воспользовавшись квазиклассической теорией Бора, получить формулу для энергии электрона Еn в однократно ионизированном атоме гелия. В чём, по вашему мнению, основной недостаток теории Бора?
2. Пользуясь энергетической диаграммой для атома водорода, представленной на рисунке 4.1, определите энергию ионизации атома водорода. Определить по той же диаграмме первый потенциал возбуждения атома водорода.
3. Что такое линейчатый и сплошной спектр? Какой спектр вы наблюдали в этом опыте?
4. Почему спектр водорода и других газов линейчатый, а спектр лам- пы накаливания сплошной?
5. Получите обобщенную формулу Бальмера (4.8) и выражение R теоретически через основные константы.
6. Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на основной.
7. Во сколько раз минимальная длина волны в серии Пашена спектра водорода больше максимальной длины волны в серии Бальмера?
8. Вычислить наибольшие длины волн в сериях Лаймана, Бальмера, Пашена в спектре водорода.
9. Объясните причины размытия энергетических уровней электрона в атоме. Какой уровень будет «размыт» в наименьшей степени. Почему?
10. Какой метод возбуждения атомов для получения спектра используется в данной установке? Объясните методику эксперимента: необходимость монохроматора, принцип его устройства, принцип работы излучателя.
ЛАБОРАТОРНАЯ РАБОТА № 5
ИЗУЧЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
ЦЕЛЬ РАБОТЫ:
Исследовать законы теплового излучения.
КРАТКАЯ ТЕОРИЯ
Тепловое излучение – это электромагнитное излучение, испускаемое веществом и возникающее за счет его внутренней энергии (в отличие, например, от люминесценции, которая возбуждается внешними источниками энергии). Термин «тепловое излучение» возник в связи с тем, что испускание энергии происходит при нагревании тела или среды. Человеком тепловое излучение воспринимается как тепло или свет. Основной особенностью теплового излучения является его равновесный характер. Так как источником теплового излечения является внутренняя энергия тел, то постоянство температуры нагретого тела можно поддерживать двумя способами:
1. За счет поглощения излучающим телом теплового излучения из окружающего пространства;
2. В результате непосредственной передачи энергии телу при механическом контакте с более нагретыми телами.
Если температура излучающего тела поддерживается постоянной первым способом, то говорят, что тело находится в состоянии термодинамического равновесия с окружающей средой. Законы теплового излучения строго справедливы именно для такого равновесия.
Фундаментальным понятием при рассмотрении теплового излучения твердых тел является понятие об абсолютно черном теле (АЧТ). Абсолютно черным называется тело, поглощающее все падающие на него излучения любых длин волн. Соответственно, при данной температуре АЧТ излучает максимально возможное (предельное) количество энергии. В природе таких источников не существует, однако есть материалы, обладающие коэффициентом поглощения А, близким к 100 %. Например, для черного бархата, сажи, платиновой черни А=99%. Каждый тепловой излучатель испускает в единицу времени с единичной площадки при заданной температуре в любом спектральном интервале меньшее количество энергии, чем АЧТ при тех же условиях. Однако возможно построение источников теплового излучения, весьма близких по своим излучательным характеристикам к характеристикам АЧТ. Простейшей моделью АЧТ может служить замкнутая полость с непроницаемыми стенками и малым выходным отверстием.
Тепловое излучение имеет сплошной спектр, положение максимума которого зависит от температуры вещества. С ее повышением возрастает общая энергия испускаемого теплового излучения, а максимум перемещается в область малых длин волн. Тепловое излучение описывается следующими характеристиками:
1) излучательность или энергетическая светимость
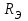 – энергия, испускаемая единицей поверхности излучаемого тела по всем направлениям за единицу времени,
– энергия, испускаемая единицей поверхности излучаемого тела по всем направлениям за единицу времени, 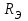 = = 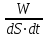 , , | | (5.1) |
2) спектральная плотность излучательности Eλ,T– количество энергии электромагнитного излучения данной длины волны λ или частоты ν испускаемого за единицу времени по всем направлениям единицей поверхности тела, имеющего температуру Т,
| E λ ,T = 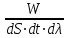 , , | | (5.2) |
3) поглощательная способность (или коэффициент поглощения) Аλ ,Т - величина, показывающая, какая часть энергии излучения с длиной волны λ, достигающая за единицу времени поверхности тела, имеющего температуру Т, поглощается им,
| Аλ ,Т = 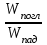 , , | | (5.3) |
В теории теплового излучения вводится понятие абсолютно черного тела – тела, которое полностью поглощает весь падающий на него поток излучения. Коэффициент поглощения Аλ ,Т абсолютно черного тела равен единице и не зависит от длины волны излучения. Интенсивность излучения абсолютно черного тела выше, чем нечерных тел при той же температуре.
Законы теплового излучения:
1) Тепловое излучение любых тел подчиняется закону Кирхгофа: отношение испускательной способности Eλ,T тел к их поглощательной способности Аλ, Т не зависит от природы излучающего тела, а зависит только от длины волны излучения λ и абсолютной температуры Т и равно излучательной способности абсолютно черного тела
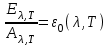 , , | | (5.4) |
2) Закон Стефана-Больцмана: энергетическая светимость абсолютно черного тела Rэ прямо пропорциональна четвертой степени температуры Т,
| Rэ = σТ4, | | (5.5) |
где σ = 5,71·10-8 Вт·м-2·град-4 – постоянная Стефана-Больцмана;
3) закон смещения Вина: длина волны λmax, на которую приходится максимум спектральной плотности энергетической светимости, обратно пропорциональна величине температуры поверхности излучения
| λmax = 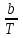 (6), где b = 2,398·10-3 м·К; (6), где b = 2,398·10-3 м·К; | | (5.6) |
5) Закон излучения Планка описывает спектральное распределение излучательности абсолютно черного тела:
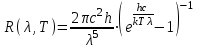 , , | | (5.7) |
где h = 6,626∙10-34 Дж∙с – постоянная Планка; T – абсолютная температура, K; c = 2,998∙108 м/с – скорость света в вакууме; k = 1,380∙10-23 Дж/К – постоянная Больцмана, λ - длина волны излучения.
Область спектра электромагнитных волн, соответствующую тепловому излучению, принято разделять на следующие спектральные диапазоны: ультрафиолетовый (0,20 – 0,40 мкм), видимый (0,40 – 0,72 мкм) и три инфракрасных – ближний (0,72 – 2,50 мкм), средний (2,50 – 25 мкм) и дальний (25 – 1000 мкм).
Величина R(λ,T) называется также монохроматической испускательной способностью и зависит от длины волны и абсолютной температуры излучающего тела. Изотермы спектральной плотности излучения АЧТ в диапазоне температур от 500 до 900 К изображены на рис. 5.1. Пунктирная кривая на рис. 5.1 является геометрическим местом максимумов, смещающихся с увеличением температуры в сторону коротких длин волн.
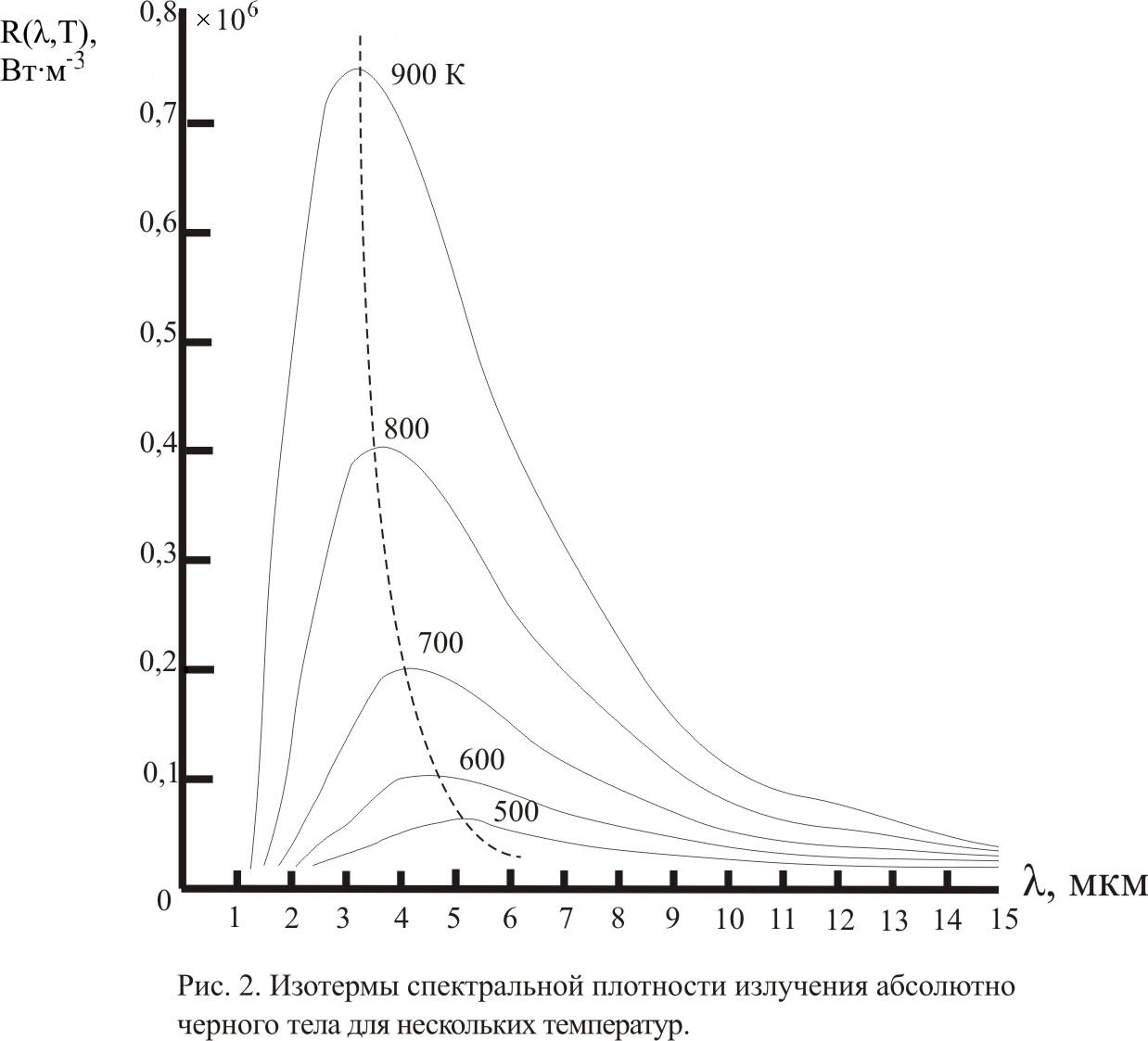
Рис. 5.1. Изотермы спектральной плотности излучения абсолютно
черного тела для нескольких температур
Они представляют собой плавные кривые с одним максимумом, спадающие до нуля при стремлении λ к 0 и к бесконечности.
Энергетическая светимость реальных тел
 , как отмечалось выше, всегда меньше энергетической светимости абсолютно черного тела
, как отмечалось выше, всегда меньше энергетической светимости абсолютно черного тела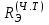 при той же температуре. Отношение
при той же температуре. Отношение 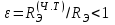 , , | | (5.8) |
является безразмерной физической величиной и называется