ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 182
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. Зависимость сечения возбуждения атомов ртути либо инертного газа от энергии электрона;
4. Разброс продольной составляющей скорости электронов после неупругого столкновения, величина которой определяет возможность преодоления задерживающего поля анод-сетка.
Приборы и оборудование.
Метод возбуждения атомов потоком электронов особенно пригоден для инертных газов и паров металла, поскольку атомы этих веществ не обладают электронным сродством, т.е. не проявляют склонности к захвату электронов и образованию отрицательных ионов. В данной работе используется трехэлектродная лампа с парами ртути.
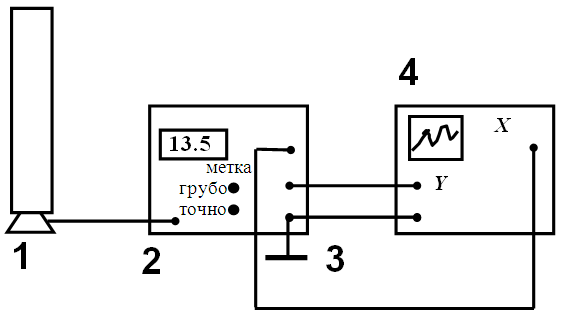 | Эксперимент Франка-Герца можно сделать более наглядным, если применить осциллографический метод снятия вольт-амперной характеристики (рисунок 2.3). В этом случае на участок сетка-катод триода 1 от блока управления 2 подаётся пилообразное напряжение некоторой частоты. |
| Рис.2.3. Блок-схема опыта Франка и Герца |
Это же напряжение подается на вход Х 3 осциллографа 4, создавая развёртку луча на экране. На вход У осциллографа подаётся напряжение, пропорциональное анодному току триода. Тогда зависимость У(Х) в определенном масштабе представляет собой искомую функциональную связь I = f(U). Масштабы изображения по осям Х и У можно легко изменять, пользуясь соответствующими регулировками усиления осциллографа. В результате на экране наблюдается вольт-амперная характеристика триода, повторяющая форму рисунка 2.2.
Порядок выполнения работы.
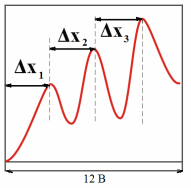 | Для наблюдения вольт-амперной характеристики лампы используется осциллограф С1-112 в режиме временной развертки. Напряжение развертки (т.е. напряжение на направляющих пластинах, которое переводит электронный луч из крайнего левого в крайнее правое положение), равно 12 В. Для вычисления масштабного коэффициента напряжения по оси абсцисс необходимо составить пропорцию:  , |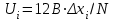
| Рис.2.4. Вид осциллограммы в опыте Франка и Герца |
где N – число клеток экрана осциллографа по оси абсцисс.
1. Включить источник питания 2 в цепи сетка-анод. Установить напряжение UСА = 2,5 В).
2. Включить осциллограф в сеть. Установить на передней панели осциллографа масштабные коэффициенты
, 
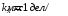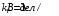. 3. С помощью осциллограммы определить первый и второй потенциал возбуждения, как показано на рис.2.4, и заполнить таблицу 2.2. Оценить погрешности δх и δU как погрешность прямых измерений, а δλ – как погрешность косвенных измерений.
Таблица 2.2.
| Δх1 | Δх2 | U1 | U2 | < Δх > | | δх | δU | λ | δλ |
| | | | | | | | | | |
4. Используя формулу
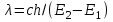и зная величину первого потенциала возбуждения, определить длину волны испускаемого атомами ртути излучения.Вопросы и задания для самоконтроля
-
В чем сущность опытов Франка и Герца? -
Какие основные выводы можно сделать на основании опытов Франка и Герца? -
Какие столкновения электронов с атомами называются упругими и неупругими? На каких участках графика вольт-амперной характеристики имеют место упругие, а на каких – неупругие столкновения? -
С какой целью на анод подается задерживающее напряжение, и из каких соображений оно выбирается? -
Что такое первый потенциал возбуждения? Какое состояние атома называется основным, а какое – возбужденным? -
Чем объясняется тот факт, что даже при отсутствии подачи ускоряющего напряжения UСК наблюдается анодный ток в цепи нагрузки? -
В чем причина возникновения смещения графиков UR= f(UСК) с изменением величины задерживающего напряжения? -
При каком ускоряющем потенциале будет наблюдаться резкое падение анодного тока в аналогичном опыте, если лампу заполнить атомарным водородом? -
Почему не наблюдается свечения ртути в объеме лампы несмотря на то, что возбужденные атомы снова переходят в основное состояние и при этом испускают кванты электромагнитной энергии? -
Почему на данной установке невозможно измерить третий, четвертый и т.д. потенциалы возбуждения ртути?
ЛАБОРАТОРНАЯ РАБОТА № 3
ФОТОЭФФЕКТ
ЦЕЛЬ РАБОТЫ:
Изучение основных законов внешнего фотоэффекта на основе измерения световой и вольтамперной характеристик вакуумного фотоэлемента.
КРАТКАЯ ТЕОРИЯ
Фотоэлектрический эффект был открыт в 1887 году немецким физиком Г.Герцем и в 1888–1890 годах экспериментально исследован А.Г.Столетовым. Наиболее полное исследование явления фотоэффекта было выполнено Ф.Ленардом в 1900 г. К этому времени уже был открыт электрон (1897 г., Дж. Томсон), и стало ясно, что внешний фотоэффект состоит в вырывании электронов из вещества под действием падающего на него света.
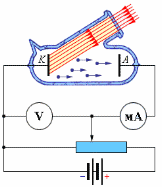 | В экспериментах Столетова использовался стеклянный вакуумный баллон с двумя металлическими электродами, поверхность которых была тщательно очищена (рис.3.1). К электродам прикладывалось некоторое напряжение U, полярность которого можно было изменять с помощью двойного ключа. Один из электродов (катод K) через кварцевое окошко освещался монохроматическим светом некоторой длины волны λ. При неизменном световом потоке снималась зависимость силы фототока I от приложенного напряжения. |
| Рис.3.1. Установка для наблюдения фотоэффекта |
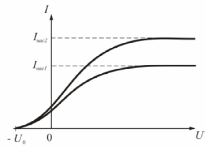
На рис.3.2 изображены типичные кривые такой зависимости, полученные при двух значениях интенсивности светового потока, падающего на катод. По мере увеличения напряжения U фототок постепенно возрастает, т.е. все большее количество фотоэлектронов достигает анода. Пологий характер кривых показывает, что электроны вылетают из катода с различными скоростями. Максимальное значение тока Iнас – фототок насыщения – определяется таким значением U, при котором все электроны, испускаемые катодом, достигают анода:
Iнас. = en, где n – число электронов, испускаемых катодом в 1 секунду, e заряд электрона.
 | Столетовым были установлены три закона:
|
| Рис. 3.2. Вольт-амперная характеристика фотоэлемента |
-
максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой v. -
Для каждого вещества существует красная граница фотоэффекта, т. е. минимальная частота v0 света (зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.
Тщательные измерения показали, что ток насыщения Iн прямо пропорционален интенсивности падающего света.
Трудности объяснения фотоэффекта
Как можно было бы объяснить фотоэффект с точки зрения классической электродинамики и волновых представлений о свете? Известно, что для вырывания электрона из вещества требуется сообщить ему некоторую энергию A, называемую работой выхода электрона. В случае свободного электрона в металле - это работа по преодолению поля положительных ионов кристаллической решётки, удерживающего электрон на границе металла. В случае электрона, находящегося в изолированном атоме, работа выхода есть работа по разрыву связи электрона с ядром. В переменном электрическом поле световой волны электрон начинает совершать колебания. И если энергия колебаний превысит работу выхода, то электрон будет вырван из вещества.
Однако в рамках таких представлений невозможно понять второй и третий законы фотоэффекта. Действительно, почему кинетическая энергия выбитых электронов не зависит от интенсивности излучения? Ведь чем больше интенсивность, тем больше напряжённость электрического поля в электромагнитной волне, тем больше сила, действующая на электрон, тем больше энергия его колебаний и с тем большей кинетической энергией электрон вылетит из катода. Логично? Логично. Но эксперимент показывает иное.
Откуда берётся красная граница фотоэффекта? Чем «плохи» низкие частоты? Казалось бы, чем больше интенсивность света, тем больше сила, действующая на электроны; поэтому даже при низкой частоте света электрон рано или поздно будет вырван из вещества — когда интенсивность достигнет достаточно большого значения. Однако красная граница ставит жёсткий запрет на вылет электронов при низких частотах падающего излучения.
Кроме того, непонятна безынерционность фотоэффекта. При освещении катода излучением сколь угодно слабой интенсивности (с частотой выше красной границы) фотоэффект начинается мгновенно — в момент включения освещения. Между тем, казалось бы, электронам требуется некоторое время для «расшатывания» связей, удерживающих их в веществе, и это время «раскачки» должно быть тем больше, чем слабее падающий свет. Аналогия такая: чем